Наращение по учетной ставке
Из формул дисконтирования легко вывести формулу наращения по учетной ставке:
S(T) = S(o) 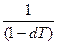
Как видно, учетная ставка не может принимать любое значение, необходимо, чтобы выполнялось неравенство (1 – dT) > 0, или d < 1/T.
На практике учетные ставки применяются при учете векселей банком. (См. раздел Хрестоматии ЭУМК).
Формулы дисконтирования по процентной и учетной ставкам приведены в соответствующей таблице Справочника ЭУМК).
Теория процентных ставок нашла широкое применение в банковских операциях, например, при учете векселей или выдачи ссуды. В частности на основе приведенных формул можно составить план погашения задолженности. Рассмотрим задачу погашения кредита в рассрочку равными суммами .
Пример 6.
Пусть кредит 250000 руб. выдан на пять лет под 30% годовых. Долг погашается равными частями, проценты начисляются на оставшуюся сумму долга один раз в год и выплачиваются вместе в выплатой основного долга.
Решение:
В данном примере ежегодная сумма погашения долга равна 50000 руб. В первый год будут начислены проценты в размере 250000х0,3=75000(руб.) и сумма, подлежащая уплате составит 125000 руб. Во втором году остаток долга составит 200000 руб., на него начисляются проценты в сумме 60000 руб. и сумма, подлежащая уплате, составит 110000 руб. Для третьего года и последующих лет расчеты проводятся аналогично. План погашения займа можно оформить в виде таблицы 1.
Таблица 1
План погашения кредита равными суммами (руб.)
| Год | Остаток долга | Погашение основного долга | Проценты | Срочная уплата |
| Итого: | - |
Как видно из таблицы 1 сумма начисленных процентов включается ежегодно в сумму, подлежащую уплате и общая сумма выплат составит 475000 руб.
Контрольные вопросы
1. Дайте определение процентной ставки. Как с помощью процентной ставки определить сумму начисленных процентов?
2. Что такое конверсионный период? Какой период времени может быть выбран в качестве конверсионного периода?
3. Дайте характеристику декурсивному и антисипативному способу начисления процентов.
4. В чем сущность наращения по простым процентам? Выведите формулу наращения по простым процентам.
5. В чем сущность дисконтирования по простым процентам? Назовите различие между математическим дисконтированием и банковским учетом.
ГЛАВА 2. СЛОЖНЫЕ ПРОЦЕНТЫ
Во второй главе рассмотрены вопросы теории сложных процентов. Основная цель данной главы – показать отличие простых процентов от сложных и обосновать возможность применения формул наращения по сложной процентной ставке в финансовых расчетах. В главе рассмотрены следующие вопросы:
1. Начисление процентов по сложной годовой процентной ставке. Капитализация процентов. Переменные ставки сложных процентов.
2. Начисление процентов m раз в году. Номинальная и эффективная ставки процентов.
3. Сравнение простых и сложных процентов.
4. Дисконтирование по сложной процентной ставке.
5. Дисконтирование по сложной учетной ставке.
6. Наращение по сложной учетной ставке.
