ГЛАВА 4. Корреляционно-регрессионный анализ влияния различных факторов на динамику развития социально-экономических явлений и процессов.

Создадим таблицу исходных данных (таблица 1.1). Построим корреляционную модель связи Потребления мяса (У) с включением факторов – потребление мяса на душу населения (Х1), среднедушевой доход(Х2),доходы (Х3),численность населения(Х5).

Таблица 1 Исходные данные для корреляционно-регрессионного анализа.

№ региона	Регионы РФ	Потребление мяса всего за год (кг) У	Потребление мяса на душу населения в год (кг) Х1	Среднедушевой доход тыс.руб. Х2	Среднедушевые ден.расходы на душу населения тыс,руб Х3
	Белгородская область	12171,6			127,279
	Брянская область	2964,6			273,621
	Владимирская область				214,207
	Воронежская область	10958,4			89,225
	Ивановская область				354,194
	Калужская область	4567,2			221,705
	Костромская область	668,8			832,632
	Курская область	4015,8			252,474
	Липецкая область	8128,2			134,160
	Московская область				56,804
	Орловская область	2804,5			366,676
	Рязанская область	3132,9			257,307
	Смоленская область	3272,4			243,729
	Тамбовская область	4067,2			207,195
	Тверская область				164,793
	Тульская область	4501,2			211,543
	Ярославская область	5382,3			208,126
	Республика Карелия	57330,8			18,801
	Республика Коми	2257,2			781,818
	Архангельская область	10213,1			100,208
	Вологодская область	8791,2			105,098
	Калининградская область	3212,1			408,475
	Ленинградская область				124,347
	Мурманская область				351,797
	Новгородская область				51,122
	Псковская область	4240,8			227,563
	Республика Адыгея	2306,9			312,941
	Республика Калмыкия	2676,8			315,481
	Краснодарский край	21432,8			56,703
	Астраханская область	1219,1			876,707
	Волгоградская область	678,9			1518,495
	Ростовская область	45305,4			21,448
	Республика Дагестан	2404,5			221,441
	Республика Ингушетия				95,198
	Кабардино-Балкарская Республика	7899,9			72,402
	Карачаево-Черкесская Республика	8498,7			77,324
	Республика Северная Осетия - Алания	274,5			2939,556
	Чеченская Республика	1150,5			143,785
	Ставропольский край				922,357
	Республика Башкортостан	1413,7			837,773
	Республика Марий Эл				215,084
	Республика Мордовия	7789,1			103,608
	Республика Татарстан	11463,8			98,204
	Удмуртская Республика	1489,6			467,030
	Чувашская Республика	2749,4			233,584
	Пермский край	23938,2			50,303
	Кировская область	4019,4			219,787
	Нижегородская область	3607,5			294,739
	Оренбургская область	8569,6			100,060
	Пензенская область	2192,4			335,979
	Самарская область	14410,5			91,470
	Саратовская область				105,850
	Ульяновская область	3939,9			226,007
	Курганская область	14902,5			68,450
	Свердловская область				219,742
	Тюменская область	4449,6			453,867
	Челябинская область				596,929
	Республика Алтай	23429,7			36,029
	Республика Бурятия	72553,6			10,804
	Республика Тыва	11510,4			57,626
	Республика Хакасия	778,8			1082,712
	Алтайский край				266,488
	Забайкальский край				2010,000
	Красноярский край	2362,2			473,675
	Иркутская область				211,370
	Кемеровская область	3250,8			298,760
	Новосибирская область	24008,1			52,945
	Омская область				109,203
	Томская область	19808,8			67,072
	Республика Саха (Якутия)	10089,1			162,027
	Камчатский край	5581,1			322,221
	Приморский край	7846,3			170,236
	Хабаровский край				136,187
	Амурская область	2399,8			416,095
	Магаданская область	24220,8			98,739
	Сахалинская область	9011,7			175,880
	Еврейская автономная область	6529,6			123,774
	Чукотский автономный округ	1020,6

Выполним корреляционно-регрессионного анализа с использованием ПП EXCEL. Для удобства анализа разобьем результаты статистической обработки на отдельные фрагменты.

Таблица 2 Корреляционная матрица

	У	Х1	Х2	Х3
У
Х1	0,126879
Х2	0,107805	0,004594
Х3	-0,35285	-0,00447	0,142501

Корреляционная матрица (таблица 1.2) содержит частные коэффициенты корреляции. Коэффициенты второго столбца матрицы характеризуют степень тесноты связи между результативным (У) и факторными признаками (Х1, Х2). Например, связь потребления мяса и долей населения в трудоспособном возрасте (r_УХ1 = 0,127) прямая, сильная; связь между ВРП на душу населения и численностью экономически активного населения (r_УХ2 = 0,108) прямая, сильная. Коэффициенты корреляции между факторами свидетельствуют об отсутствии мультиколлинеарности.

Таблица 3 Регрессионная статистика

Множественный R	0,406819
R-квадрат	0,165502
Нормированный R-квадрат	0,131671
Стандартная ошибка	11500,68
Наблюдения

Множественный коэффициент корреляции R = 0,41 показывает, что теснота связи между потреблением мяса и факторами, включенными в модель, сильная. Множественный коэффициент детерминации (R-квадрат) D = 0,13 , т.е. 13% вариации уровня рентабельности объясняется вариацией изучаемых факторов.

Таблица 4 Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия			647046314,9	4,892017	0,003711
Остаток			132265740,3
Итого

Проверим значимость коэффициента множественной корреляции, для этого воспользуемся F-критерием, для чего сравним фактическое значение F с табличным значением F_табл. При вероятности ошибки α = 0,05 и степенях свободы v1=k-1=3-1=2, v2=n-k=77-3=74 где k – число факторов в модели, n – число наблюдений, F_табл = 2,0003. Так как F_факт = 152,58 > F_табл = 2,0003, то коэффициент корреляции значим, следовательно, построенная модель в целом адекватна.

Таблица 5 Коэффициенты регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-2101,659	8384,903	-0,251	0,803	-18808,943	14605,624	-18808,943	14605,624
Переменная X 1	129,053	110,112	1,172	0,245	-90,348	348,455	-90,348	348,455
Переменная X 2	0,374	0,250	1,498	0,138	-0,124	0,872	-0,124	0,872
Переменная X 3	-9,566	2,735	-3,497	0,001	-15,016	-4,115	-15,016	-4,115

Используя таблицу 1.5 составим уравнение регрессии:

У = -2101,659+ 129,053Х₁ -0,374Х₂ -9,566Х3.

Интерпретация полученных параметров следующая:

а0 = -2101,659– свободный член уравнения регрессии, содержательной интерпретации не подлежит;

а1= 129,053 – коэффициент чистой регрессии при первом факторе свидетельствует о том, что при увеличении потребления мяса на душу населения потребление мяса за год уменьшится на 0,27%, при условии, что другие факторы остаются постоянными;

а2 =0,374– коэффициент чистой регрессии при втором факторе свидетельствует о том, что при увеличении среднедушевого дохода потребление мяса за год увеличится на 0,46 %, при условии, что другие факторы остаются постоянными;

Проверку значимости коэффициентов регрессии осуществим с помощью t-критерия Стьюдента; для этого сравним фактические значения t-критерия с табличным значением t-критерия. При вероятности ошибки α = 0,05 и степени свободы v= n-k-1=88-3-1 =84, где k – число факторов в модели, n – число наблюдений, tтабл = 2,01. Получим

t1факт = -0,251 < tтабл = 2,01,

t2факт = 1,172< tтабл = 2,01,

t3факт = 1,498< tтабл = 2,01.

t4факт = -3,497< tтабл = 2,01.

Значит, статистически значимыми являются только один фактор. В этом случае модель пригодна для принятия решений, но не для прогнозов.

Таблица 6 Описательная статистика

У	У	Х2	Х3
Среднее	1329,2	18964,8	20898,8
Стандартная ошибка	4293,03	9582,57	13820,76
Медиана	69,2	17,4	6,4
Мода	26,6	19,2	3,2
Стандартное отклонение	40272,18	89892,52	129650,2.
Дисперсия выборки	36073,37	63,78873	30,09499
Эксцесс	19,48722	3,498715	0,287114
Асимметричность	3,950452	1,947545	0,854547
Интервал	1291,1		23,7
Минимум	4,5	11,8	0,2
Максимум	1295,6	47,8	23,9
Сумма	10815,5	1612,3	615,4
Счет

Средние значения признаков, включенных в модель У = 1329,2 %; Х1 = 18964,8 тыс.руб; Х2 = 20898,8 тыс.руб.

Стандартные ошибки коэффициентов регрессии Sа0 = 4293,03; Sа1 =9582,57; Sа2 = 13820,76.

Средние квадратические отклонения признаков σУ = 40272,18%; σХ1 = 89892,52 ; σХ2 = 129650,2.

Зная средние значения и средние квадратические отклонения признаков, рассчитаем коэффициенты вариации для оценки однородности исходных данных

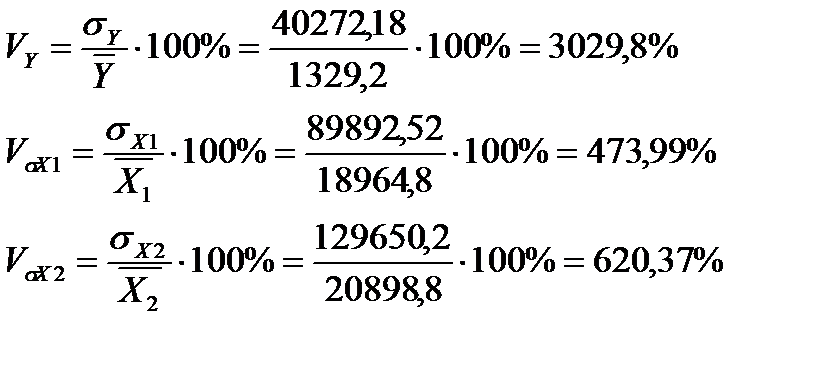
Вариация факторов, включенных в модель превышает допустимых значений (33-35%), а потребление мяса вариацией 3029,8 %. В данном случае необходимо проверить исходную информацию и исключить те значения, которые значительно отличаются от средних значений.

Разные единицы измерения делают несопоставимыми коэффициенты регрессии, когда возникает вопрос о сравнительной силе воздействия на результативный признак каждого из факторов чистой регрессии. Выразим их в стандартизированной форме в виде бета-коэффициентов и коэффициентов эластичности.

Каждый из β-коэффициентов показывает, на сколько средних квадратических отклонений изменится сальдированный финансовый результат, если соответствующий фактор изменится на свое среднее квадратическое отклонение.

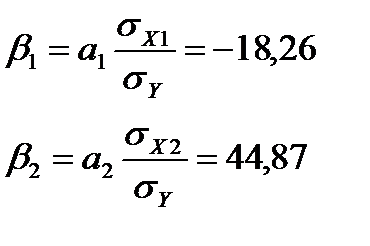
При увеличении доли населения в трудоспособном возрасте на 1 свое среднее квадратическое отклонение потребление мяса на доход уменьшится на 18,26 ; и при увеличении численности экономически активного населения на 1 среднее квадратическое отклонение потребление мяса доход увеличится на 44,87 своего среднего квадратического отклонения.

Сопоставление β-коэффициентов показывает, что наиболее сильное влияние на варьирование потребление мяса первым оказывает –доход, вторым –численность населения.

Каждый из коэффициентов эластичности показывает, на сколько процентов изменится в среднем потребления мяса, если соответствующий фактор изменится на 1%.

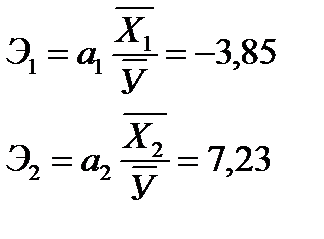
При увеличении среднедушевого дохода потребление мяса уменьшится на 3,85 %; при увеличении численности населения на 1 % потребление мяса увеличится на 7,23 %.

В таблице 7 приведены расчетные значения потребление мяса и отклонения фактических значений от расчетных. Расчетные значения получены путем подстановки значений факторов потребления мяса в уравнение регрессии.

Если расчетное значение потребления мяса превышает фактическое значение (остатки отрицательные), то есть резервы повышения потребления мяса за счет факторов включенных в модель, в противном случае (остатки положительные) отсутствуют резервы повышения потребление мяса за счет факторов, включенных в модель.

Таблица 7 Остатки

Наблюдение	Предсказанное Y	Остатки
	1294055,462	-839855,4619
	2000183,19	137816,8101
	292060,4118	-111660,4118
	185945,9809	-85045,98086
	623040,6505	-44340,65049
	131806,413	-4606,412964
	1009802,525	1312997,475
	389656,8236	-42056,8236
	254621,2987	-119821,2987
	1585275,26	-232875,2604
	555701,0341	-69801,03411
	169350,9507	99249,04926

Так регионы имеют резервы повышения потребления мяса. Полученную модель используем для расчета резервов роста потребления мяса . Разделим организации на две группы: первая –где потребление мяса ниже, чем в среднем по совокупности, а вторая –где потребление мяса выше, чем в среднем по совокупности. Заполним таблицу 8.

Таблица 8 Расчет резервов повышения уровня рентабельности

Фактор	Среднее значение фактора	Разность между группами	Коэффициент регрессии	Влияние факторов на сальдированный финансовый результат
		по совокупности
А				4=3-1	5=3-2		7=6*4	8=6*5
Потребление мяса на душу населения	44353,8	281706,67	18964,8	-25389	-262742	-0,27	6855,03	70940,34
Среднедушевой доход	56183,4		20898,8	-35284,6	-399946	0,46	-16230,9	-183975
Потребление мяса	-40650,4	116226,67	1329,2	41979,6	-114897	х	-9375,89	-113035

Анализируя результаты таблицы 8 видим, что в 1 группе регионов есть резерв понижения потребления мяса на 9375,89 % за счет рассматриваемых факторов. Так, если потребление на душу населения уменьшить с 44353,8 тыс.руб. до среднего по совокупности (18964,8), то численность экономически активного населения результат увеличится на 6855,03%; при снижении среднедушевого дохода уменьшится на 16230,9%.

Суммарный резерв повышения потребления мяса на душу населения и в первой и во второй группе за счет рассматриваемых факторов исчерпан.