Задания для внеаудиторной самостоятельной работы
2.1 Распределение внеаудиторной самостоятельной работы по темам
| Самостоятельная работа | ||||
| Разделы, темы | Исследовательская работа, решение задач | Написание рефератов, докладов | Создание презентаций | Разработка алгоритма |
| Раздел 1. Комбинаторика | ||||
| Тема 1.1 Элементы теории множеств | Элементы комбинаторики | Элементы комбинаторики | ||
| Раздел 2. Теория вероятностей | ||||
| Тема 2.1 Теория вероятностей | Выполнение расчетного варианта (задачи 1,2,3,4,5,6,7,8) | Основы теории вероятностей | ||
| Тема 2.2 Дискретные случайные величины | Выполнение расчетного варианта (задача 9) | Дискретные случайные величины | Решение логических задач | |
| Тема 2.3 Непрерывные случайные величины | Выполнение расчетного варианта (задача 10) | Непрерывные случайные величины | ||
| Раздел 3. Статистика | ||||
| Тема 3.1 Выборочный метод. Статистические оценки параметров распределения | Выполнение расчетного варианта (задачи 11,12,13) |
Варианты типового расчета
Условие задач
1.Докажите тождества, используя только определения операций над множествами.
2. Найдите среди указанных ниже предложений высказывания. Укажите их истинностные значения.
3. Запишите в символической форме данные высказывания, если известны p, q, r.
4. Интерпретируйте следующие выражения как обычные высказывания, если известны p, q, r.
5. Даны графы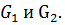 
Найдите 
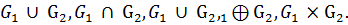Для графа 
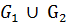найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящая из вершины 1.
6.Составить таблицы истинности формул.
7.Проверить двумя способами, будут ли эквивалентны следующиеформулы…
а) составление таблиц истинности;
б) приведение формул к СДНФ или СКНФ с помощью эквивалентных
преобразований.
8.С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина.
9.Логическая функция l (x,y) задана на множестве D={a,b} с помощью таблицы
| x | y | l(x,y) |
| a | a | Л |
| a | b | И |
| b | a | И |
| b | b | И |
Определите истинностные значения следующих формул:
10.Пусть P(x), R(x), Q(x), S(x,y) обозначают предикаты «x – простое число», «x – четное число», «x – нечетное число», «y делится на x» соответственно.
Переведите на русский язык:
11. С помощью алгебры логики докажите тождества из задания 1.
Вариант 1
1. 
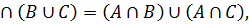A
A 
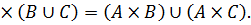
2. «Который час? »
3. «У меня нет денег и я не совершу путешествие на Марс», если р, q и r обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим.
q : Я совершу путешествие на Марс.
r : У меня есть деньги.
4. q /\г, если р, q и r обозначают следующие высказывания:
р : Эта игра очень трудна.
q : Я играю в шахматы.
r : Игра в шахматы требует времени.
5.
 |
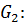| 3 2 |
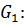
6.(x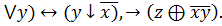 
7. x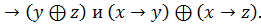 
8. (x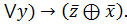 
9.∀ yl(b,y)
10.P(7)
Вариант 2
1. A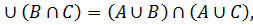 
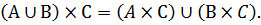
2. «Целое число 1 есть наименьшее положительное целое число»
3. «У меня нет денег и путешествие на Марс является дорогостоящим или я совершу путешествие на Марс.», если р, q и r обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим.
q : Я совершу путешествие на Марс.
r : У меня есть деньги.
4. ~р V ~q,если р, q и r обозначают следующие высказывания:
р : Эта игра очень трудна.
q : Я играю в шахматы.
r : Игра в шахматы требует времени.
5.
| |
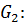| 3 2 |
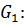
6.(x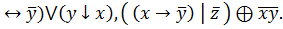 
7.x∣(y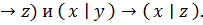 
8. 
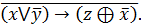
9. ∃yl(b,y)
10.∀x(S(2,x) ⊃R(x))
Вариант 3
1.A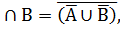 
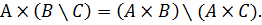
2. «Если х = 3, то х2 = 6».
3.«Неверно, что у меня есть деньги и я полечу на Марс», если р, q и r обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим.
q : Я совершу путешествие на Марс.
r : У меня есть деньги.
4.(р V r) /\q, если р, q и r обозначают следующие высказывания:
р : Эта игра очень трудна.
q : Я играю в шахматы.
r : Игра в шахматы требует времени.
| 1 2 |
| |
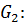| 3 2 |
| 4 3 |
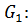
6. (x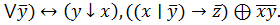 
7.x ⋀(y ⊕ z) и (x ⋀ y) ⊕ (x ⋀ z).
8.( 
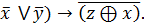
9.∀x∀ yl(x,y)
10.∃x(R(x)⋀P(x))⋀ך∃x((R(x)⋀ P(x))⋀∃y(x≠y)⋀R(y) ⋀P(y)))
Вариант 4
1. A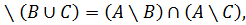 
A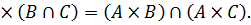 
2. «Берегись автомобиля! »
3. « Путешествие на Марс не является дорогостоящим и я полечу на Марс или путешествие на Марс является дорогостоящим и я не полечу на Марс», если р, q и r обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим.
q : Я совершу путешествие на Марс.
r : У меня есть деньги.
4.р /\ q /\r, если р, q и r обозначают следующие высказывания:
р : Эта игра очень трудна.
q : Я играю в шахматы.
r : Игра в шахматы требует времени.
5.
| 1 2 |
| |
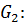| 3 2 |
| 4 3 |
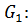
6. (x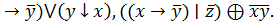 
7. x ⋀(y ⊕ z) и (x ⋀ y) ⊕ (x ⋀ z).
8. ( 
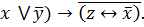
9. ∀x∃yl(x,y)
10.∀x(ךR(x) ⊃ךS(2, x))
Вариант 5
1. 
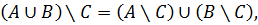
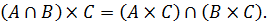
2. «Южная Дакота — южный штат».
3. «У меня есть деньги, но путешествие на Марс является дорогостоящим, и я не совершу путешествие на Марс», если р, q и r обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим.
q : Я совершу путешествие на Марс.
r : У меня есть деньги.
4. р/\ q /\ ~r, если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
| 1 2 |
| 3 2 |
| |
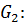| 4 3 |
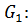
6. (x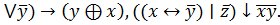 
7. x ⋀(y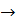 
z) и (x ⋀ y) 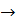(x ⋀ z).
8. 
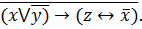
9. ∃y∀xl(x,y)
10.P(7)
Вариант 6
1.( 
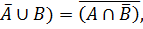
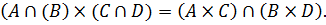
2. «Все четные числа делятся на 2».
3. «У меня не быстродействующий компьютер или я закончу проект вовремя», еслир, q и r обозначают следующие высказывания:
р : Мой компьютер быстродействующий.
q : Я окончу проект вовремя.
r : Я сдам экзамен.
4. р /\ (~q V ~r), если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
5.
| 3 2 |
| |
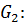| 4 3 |
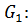
6. (x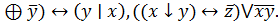 
7. x ⋀(y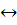 
z) и (x ⋀ y) 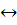(x ⋀ z).
8. 
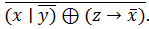
9.∀y ∃xl(x,y)
10.∀x(R(x)⋀∀y(S(x,y)⊃P(y)))
Вариант 7
1. 
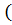A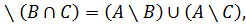 
(A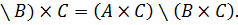 
2. «Загрузите пакеты в машину».
3.«Я не закончу проект вовремя и не сдам экзамен», еслир, q и r обозначают следующие высказывания:
р : Мой компьютер быстродействующий.
q : Я окончу проект вовремя.
r : Я сдам экзамен.
4. (р V ~q) /\r, если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
| 1 2 |
| |
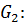| 3 2 |
| 4 3 |
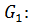
6. ( 
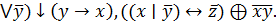x
7. x ⋀(y ∣z) и (x ⋀ y) ∣ (x ⋀ z).
8. 
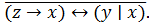
9.∀y∀xl(x,y)
10.∀x(P(x)⊃∃y(R(y) ⋀S(x,y)))
Вариант 8
1. 
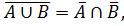
C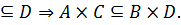 
2. «Это утверждение не может быть истинным».
3.«Неверно, что я закончу проект и сдам экзамен», еслир, q и r обозначают следующие высказывания:
р : Мой компьютер быстродействующий.
q : Я окончу проект вовремя.
r : Я сдам экзамен.
4. (р /\ r) V (q/\ ~r), если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
| 1 2 |
| |
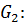| 3 2 |
| 4 3 |
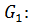
6. (x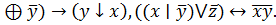 
7. x ⋁(y 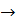z) и (x ⋁ y) 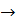(x ⋁z).
8. 
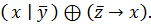
9.∃x ∃yl(x,y)
10.∀x(Q(x)⊃∀y(P(y)⊃ ךS(x,y)))
Вариант 9
1. 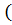A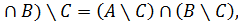 
(A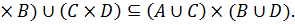 
2. «Юпитер — ближайшая к солнцу планета».
3. 
«У меня быстродействующий компьютер или я не закончу проект вовремя и сдам экзамен», еслир, q и r обозначают следующие высказывания:
р : Мой компьютер быстродействующий.
q : Я окончу проект вовремя.
r : Я сдам экзамен.
4. (р V r) /\q, если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
5.
| |
| 1 2 |
| 3 2 |
| 4 3 |
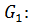
6. 
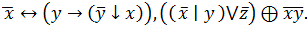
7. x ⋁(y ∣z) и (x ⋁ y) ∣(x ⋁z).
8.( 
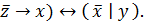
9.∃x∀yl(x,y)
10.R(2)⋀ P(2)
Вариант 10
1.A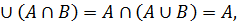 
(A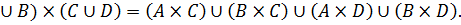 
2. «Не следует хранить компакт-диски в микроволновой печи».
3. «У меня не быстродействующий компьютер или я закончу проект вовремя и сдам экзамен» еслир, q и r обозначают следующие высказывания:
р : Мой компьютер быстродействующий.
q : Я окончу проект вовремя.
r : Я сдам экзамен.
4. р /\ q /\r, если р, q и r обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
r : У меня есть дог.
5.
| |
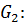| 1 2 |
| 3 2 |
| 4 3 |
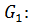
6. 
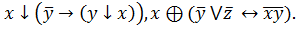
7. x ⋁(y 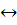z) и (x ⋁ y) 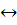(x ⋁z).
8. 
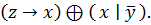
9.∃y∃xl(x,y)
10.∃x(R(x)⋀S(x,6))