Типовые примеры и методы их решения. Решение.а) Поскольку применяется сложная процентная ставка, то в формуле (112) a = 1 + r и сама формула принимает вид:
Пример 2.6.1.Платеж 10 тыс. руб. и со сроком уплаты через 4 года требуется заменить платежом со сроком уплаты через: а) 2 года; б) 9 лет. Определите величину нового платежа, если применяется сложная процентная ставка 30% годовых.
Решение.а) Поскольку применяется сложная процентная ставка, то в формуле (112) a = 1 + r и сама формула принимает вид:
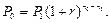
Полагая Р1=10 тыс. руб., п1= 4, n0 = 2, r = 0,3 , получим:
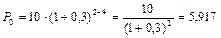 тыс. руб.
тыс. руб.
б) Так как в этом случае n0=9, то
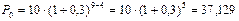 тыс. руб.
тыс. руб.
Как и следовало ожидать, с увеличением срока растет и величина нового платежа.
Естественно, решать этот пример можно было, и не используя формулу замены платежей. Так, задание первого пункта можно было сформулировать таким образом: определите сумму, которую необходимо поместить в банк под сложную процентную ставку 30% годовых, чтобы через 2 года она стала равной 10 тыс. руб., после чего применить формулу (66). Аналогичные отображения можно высказать и по вопросу второго пункта примера.
Пример 2.6.2. Платеж 20 тыс. руб. со сроком уплаты через 11 лет предполагается заменить платежом со сроком уплаты через 5 лет. Определите величину нового платежа, если применятся: а) сложная процентная ставка 32% годовых; б) сложная учетная ставка 32% годовых; в) непрерывная ставка 32% за год.
Решение. а) В этом случае, как и в предыдущем примере, пользуемся формулой 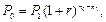 где Р1 = 20 тыс. руб., n1 = 8, n0 = 5, r =0,32:
где Р1 = 20 тыс. руб., n1 = 8, n0 = 5, r =0,32:
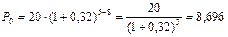 тыс. руб.
тыс. руб.
б) Так как применяется сложная учетная ставка, то в формуле (112) а = (1 – d)-1 и сама формула принимает вид:
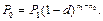
Поскольку d = 0,32,то
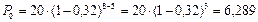 тыс. руб.
тыс. руб.
в) В случае непрерывных процентов в формуле (112) 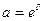 , следовательно,
, следовательно,
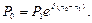
Полагая 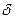 = 0,32, получим:
= 0,32, получим:
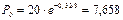 тыс. руб.
тыс. руб.
Заметим, что если в пунктах а) и б) увеличивать число начислений процентов в году, то величина нового платежа в случае а) будет уменьшаться, приближаясь к 7,658 тыс. руб., а и случае б) – увеличиваться, приближаясь также к 7,658 тыс. руб.
Пример 2.6.3. Определите величину нового срока, если платеж 15 тыс. руб. через 3 года заменяется платежом: а) 8 тыс. руб.; б) 21 тыс. руб. При расчетах учитывать возможность помещения денег под процентную ставку 28% годовых с ежеквартальным начислением сложных процентов.
Решение. Так как можно вложить деньги под сложную процентную ставку, то в формуле (113) 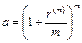 и формула принимает следующий вид:
и формула принимает следующий вид:
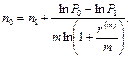
а) Поскольку в рассматриваемом случае P1=15 тыс. руб., Р0 = 8 тыс. руб., n1 = 3, m = 4 , r(m) = r(4) = 0,28, то согласно формуле:
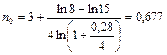 года.
года.
Таким образом, если в году 365 дней, то n0 = 247 дней.
б) Полагая Р0 =21 тыс. руб., получим:
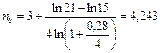 года.
года.
Таким образом, новый срок составит 4 года 89 дней. Естественно, с ростом величины нового платежа растет и его срок.
Заметим, что если в формуле (113) для сложной процентной ставки перенести n1 в левую часть равенства и обозначить Р1 = Р, Р0 = Fп, n0 – n1 = n, то получим формулу (60). Подобные суждения можно высказать и о связи формулы (113) (при соответствующих обозначениях) с формулами (71) и (79).
Пример 2.6.4. Согласно контракту господин N обязан уплатить кредитору суммы 20, 30 и 50 тыс. руб. соответственно через 1 год 6 месяцев, 2 и 4 года. Однако он хочет вернуть долг одним платежом через 3 года 6 месяцев. Найдите величину консолидированного платежа, если применяется сложная процентная ставка 36% годовых. Через какое время господин N должен выплатить весь долг, если консолидированный платеж будет равен сумме выплат по первоначальному контракту? Как изменятся результаты при ежеквартальном начислении сложных процентов?
Решение. Так как применяется сложная процентная ставка, формула (114) при а = 1 + r принимает вид:
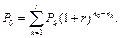
Полагая Р1 = 20 тыс. руб., P2 = 30 тыс. руб., Р3 = 50 тыс. руб., n1 = 1,5 , n2 = 2 , n3=4, n0 = 3,5 , r = 0,36 , находим величину консолидированного платежа:
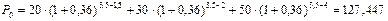 тыс. руб.
тыс. руб.
Если же господин N решает выплатить весь долг суммой 20 + 30 + 50 = 100 тыс. руб., то для определения срока выплаты воспользуемся формулой (115), где а = 1 + r и Р0 = 100 тыс. руб.:
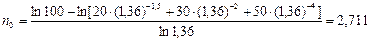 года.
года.
Обратим внимание, что срок n0 можно найти, используя уже известную величину консолидированного платежа, а именно исходя из условия, что платеж в сумме 127,447 тыс. руб. через 1 года 6 месяцев заменяется платежом в сумме 100 тыс. руб. Тогда можно воспользоваться формулой (113):
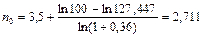 года.
года.
Естественно, получили тот же результат.
Если же в расчетах используется годовая номинальная процентная ставка r(m), то 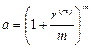 , и формула (114) принимает вид:
, и формула (114) принимает вид:
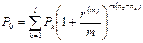
Полагая m = 4 , r(4) = 0,36, определяем выплату через 3 года 6 месяцев:
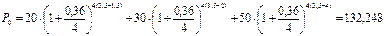 тыс. руб.
тыс. руб.
В случае выплаты всего долга в сумме 100 тыс. руб. для определения срока выплаты воспользуемся формулой (115), которая в этих условиях принимает вид:
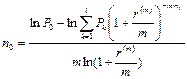
и, следовательно, искомый срок будет равен:
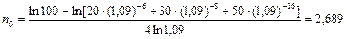 года.
года.
Конечно, этот же результат можно было получить и по формуле (113), полагая Р0=100 тыс. руб., P1=132,248 тыс. руб., n1=3,5:
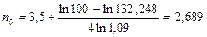 года.
года.
Пример 2.6.5. В соответствии с контрактом предприниматель обязан выплатить кредитору 12 тыс. руб. через 9 месяцев, после этого через 1 год – 15 тыс. руб. и еще через 1 год 6 меся – 18 тыс. руб. Предприниматель предлагает выплатить 30 руб. через 2 года и еще 20 тыс. руб. – через 2 года после первой выплаты. Являются ли эти контракты эквивалентными, есть возможность помещения денег в банк под номинальную процентную ставку 32% годовых с начислением сложных процентов по полугодиям?
Решение. Как известно, два контракта считаются эквивалентными, если приведенные стоимости потоков платежей по Мм контрактам одинаковы. В качестве даты приведения примем дату, от которой измеряются все сроки.
Поскольку сроки выплат по первому контракту соответственно равны 0,75 года (9 месяцев), 1,75 года (9 месяцев + 1 год), 3,25 года (9 месяцев + 1 год + 1,5 года), то сумма приведенных стоимостей потоков платежей по первому контракту составит:
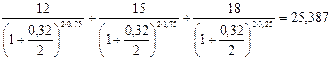 тыс. руб.
тыс. руб.
Аналогичным образом для второго контракта получим (записывая 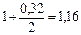 ):
):
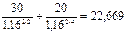 тыс. руб.
тыс. руб.
Следовательно, контракты не эквивалентны: первый контракт для кредитора выгоднее.
Пример 2.6.6. Предприниматель купил у господина N грузовой автомобиль, заключив контракт, согласно которому предприниматель должен уплатить господину N 22 тыс. руб. через 9 месяцев, 40 тыс. руб. – через 3 года и 28 тыс. руб. – через 4 года месяцев с момента покупки. Господин N хочет сразу же продать этот контракт банку. Какую сумму может заплатить банк господину N, если банк за предоставленный кредит начисляет: а) сложные проценты по годовой номинальной процентной ставке 30%; б) непрерывные проценты с силой роста 30%?
Решение.По существу необходимо решить задачу консолидации платежей: заменить платежи Р1 = 22 тыс. руб., Р2 = 40 тыс. руб., Р3 = 28 тыс. руб. со сроками соответственно n1= 0,75 года, n2 = 3года, n3 = 4,5 года одним платежом Р0 со сроком n0 =0 (т.е. сразу осуществить выплату всего долга).
а) В этом случае пользуемся формулой (114) при а = 1 + r, где r = 0,3:
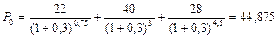 тыс. руб.
тыс. руб.
Таким образом, банк может заплатить за контракт не более 44,875 тыс. руб.
б) Так как здесь используется непрерывная ставка, то формула (114) при 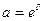 принимает вид:
принимает вид:
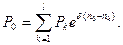
Полагая 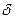 = 0,3 , определяем искомую сумму:
= 0,3 , определяем искомую сумму:
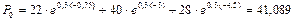 тыс. руб.
тыс. руб.
Пример 2.6.7. Согласно финансовому соглашению господин N должен выплатить банку 10 тыс. руб. через 2 года и 30 тыс. руб. – через 5 лет с момента заключения соглашения. Господин N предлагает заменить это соглашение эквивалентным: осуществить выплаты тремя равными платежами, сделав первый платеж через 1 год, второй – через 3 года 6 месяцев и третий – через 8 лет. Какой величины должен быть каждый из этих платежей, если банк на предоставленный кредит начисляет каждые полгода сложные проценты по номинальной процентной ставке 36% годовых?
Решение. Обозначим через х величину каждого нового платежа. Схематично условие задачи можно изобразить на оси времени (одно деление равно полугодию, т.е. равно периоду начисления процентов) следующим образом: над осью помещаются платежи (в тыс. руб.) по первому контракту, а под осью – по новому контракту.

















 10 30
10 30
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 t полугод.
x x x
Приведем все платежи к моменту 0 и приравняем суммы приведенных платежей по первому и по новому контрактам:
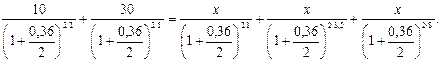
Отсюда следует:
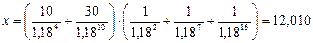 тыс. руб.
тыс. руб.
Обратим внимание, что такой же результат получим, выбрав в качестве момента приведения любой другой момент времени. Пусть, например, в качестве момента приведения выбрано начало шестого года (т.е. конец пятого года). В этом случае уравнение эквивалентности примет вид:
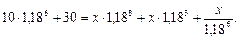
Поделив обе части уравнения на 1,1810, получим такое же уравнение, что и раньше.
Пример 2.6.8. Имеется обязательство выплатить суммы 30 тыс. руб. и 80 тыс. руб. соответственно через 2 года и 6 лет. По обоюдному согласию стороны пересматривают порядок выплат: 20 тыс. руб. выплачивается через 1 год, 40 тыс. руб. – через 4 года, остаток долга погашается через 8 лет. Определите величину третьего платежа, если в расчетах используется сложная процентная ставка 28% годовых.
Решение. Обозначим через х величину остатка долга. Изобразим схематично условие задачи на оси времени (одно деление равно одному году): над осью помещаем платежи (в тыс. руб.) по первоначальному обязательству, а под осью – по пересмотренному обязательству.










 30 80
30 80
 |
0 1 2 3 4 5 6 7 8 9 10 t лет
20 40 x
Выбирая за дату приведения момент заключения финансового соглашения, запишем уравнение эквивалентности:
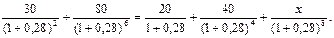
Решая это уравнение относительно x, находим х = 43,049 тыс. руб.
Глава 3 АННУИТЕТЫ
Постоянный аннуитет
Основные положения
· Одним из основных элементов финансового анализа является оценка денежного потока, генерируемого в течение ряда временных интервалов в результате реализации какого-либо проекта или функционирования того или иного вида активов. Обычно считается, что генерируемые в рамках одного временного интервала поступления имеют место либо в его начале, либо в его конце, т.е. они не распределены внутри интервала, а сконцентрированы на одной из его границ. В первом случае поток называется потоком пренумерандо или авансовым, во втором – потоком постнумерандо.
· Оценка денежного потока может выполняться в рамках решения двух задач: а) прямой, предполагающей суммарную оценку наращенного денежного потока; б) обратной, предполагающей суммарную оценку дисконтированного (приведенного) денежного потока.
· Ключевым моментом при оценке денежного потока является молчаливая предпосылка о том, что анализ ведется с позиции разумного инвестора", т.е. инвестора, не просто накапливающего полученные денежные средства, а немедленно инвестирующего их с целью получения дополнительного дохода. Именно этим объясняется тот факт, что при оценке потоков в обоих случаях (и при наращении, и при дисконтировании) предполагается капитализация обычно по схеме сложных процентов.
· Аннуитет (финансовая рента) представляет собой частный случай денежного потока, а именно это однонаправленный денежный поток с равными временными интервалами. Любой элемент такого денежного потока называется членом аннуитета (членом ренты), а величина постоянного временного интервала между двумя его последовательными элементами называется периодом аннуитета (периодом ренты).
· Если число равных временных интервалов ограниченно, аннуитет называется срочным. Если в течение каждого базового периода начисления процентов денежные поступления происходят р раз, то аннуитет часто называют р -срочным. Часто в качестве такого базового периода выступает календарный год.
· Аннуитет называется постоянным, если все денежные поступления равны между собой. В этом случае формулы для оценки будущей и приведенной стоимости аннуитета существенно упрощаются. Значения коэффициента наращения аннуитета, входящего в формулу определения будущей стоимости, табулированы для различных значений процентной ставки и сроков действия аннуитета. Также табулированы значения коэффициента дисконтирования аннуитета, входящего в формулу определения приведенной стоимости.
· Ситуацию, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода, можно рассматривать с двух точек зрения: на отдельные взносы, поступающие в течение периода, начисляются либо сложные, либо простые проценты.
· Аннуитет называется отсроченным, если начало его первого периода сдвинуто вправо по временной оси от момента времени, на который происходит анализ.
· Аннуитет называется бессрочным (или вечной рентой), если число его элементов неограниченно большое (в том числе достаточно большое). В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют и вечной рентой.
