Занятие 2. Простые учетные ставки
Учетная ставка рассчитывается отношением наращения (F-P) к ожидаемой в будущем к получению, или наращенной, величине F.
Схемапростых процентов предполагает неизменность базы,с которойпроисходит начисление.
Банковское (коммерческое) дисконтирование применяется в ситуации предварительного начисления простого процента, например, при операции по учету векселя, заключающейся в покупке банком векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю на дату его погашения. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.
Банковское дисконтирование нельзя осуществить во всех ситуациях, например, по достаточно большой учетной ставке и задолго до срока платежа.
Возможно финансовое соглашение, предусматривающее изменение во времени учетной ставки.
При применении наращения по простой учетной ставке величина начисляемых процентов с каждым годом увеличивается. Простая учетная ставка обеспечивает более быстрый рост капитала, чем такая же по величине процентная ставка.
Цель проведения занятия- научиться проводить расчеты по схеме простых учетных процентов, используя формулы финансовых вычислений.
Основные формулы
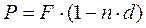 (2.1)
(2.1)
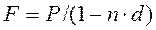 (2.2)
(2.2)
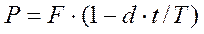 (2.3)
(2.3)

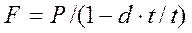 (2.4)
(2.4)
D=F-P=F×n×d (2.5)
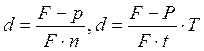 (2.6)
(2.6)
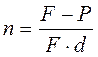 (2.7.)
(2.7.)
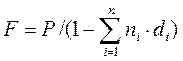 (2.8)
(2.8)
где
P- вложенная сумма (сумма, которую получает владелец векселя при его учете) ;
F – наращенная сумма (номинальная стоимость векселя);
n- количество периодов продолжительности финансовой операции;
d-простаяучетная ставка;
t -продолжительность финансовой операции в днях;
T- количество дней в году;
D- дисконт.
Типовые задачи с решениями
Задача 1.В банк 6 мая предъявлен для учета вексель, на сумму 140 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, считая, что в году 365 дней. Определить сумму, получаемую векселедержателем от банка, и комиссионные, удерживаемые банком за свою услугу. За какое время до срока платежа операция учета векселя имеет смысл?
Решение
По формуле (2.1) при F = 140.; n = 65/365, d = 0,4 получим:
Р = 140×(1-0,4 ×65/365)=129, 89
Векселедержатель получит от банка 129,89 тыс. руб.
Комиссионные банка ( или дисконт) определяются по формуле D= F - P
D= F - P= 140-129, 89=10, 11 тыс. руб.
Комиссионные, удерживаемые банком за свою услугу, равны 10,11 тыс. руб.
Учет векселя по учетной ставке имеет смысл при n<1/d, для этой задачи при n< 2,5 года. При n>2,5 года сумма Р, которую должен получить владелец векселя при его учете, становится отрицательной.
Задача 2.Кредит в размере 400 тыс. руб. выдан по простой учетной ставке 25% годовых. Определить срок кредита, если заемщик планирует получить на руки 350 тыс. руб.
Решение
По формуле (2.7. ) при F =400 ; Р=350; d=0,25 получаем:
n = (400-350)/(400×0,25)=0,5
Срок кредита равен 0,5 года.
Задача 3.Вексель на сумму 900 тыс. руб. учитывается по простой учетной ставке за 120 дней до погашения с дисконтом 60 тыс. руб. в пользу банка. Определить величину годовой учетной ставки при временной базе 360 дней в году.
Решение.
По формуле (2.6) при F=900; F-P=60; t=120; T=360 дней, получим :
d= 60×360/(900×120)=0,20=20%
Годовая учетная ставка при временной базе 360 дней в году равна 20% годовых.
Задача 4.В банк предъявлен вексель на сумму 500 тыс. руб. за полтора года до его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установленной следующим образом: первые полгода – 30% годовых, следующие полгода- 36% годовых, затем каждый квартал ставка повышается на 2%. Определите дисконт банка и сумму, которую получит векселедержатель.
Решение.
По формуле (2.8) вычислим множитель наращения:
1- ( 0,5 × 0,30 +0,5 × 0,36 + 0,25 × 0,38 + 0,25 × 0,4) = 0, 475
Р = 500 × 0,475 = 237,50
Сумма, полученная владельцем векселя равна 237 500 руб.
По формуле 1.11 дисконт равен D = 500- 237,5 = 262,5
Дисконт банка равен 262 500 руб.
Задача 5.Банк 1 января учел два векселя со сроками погашения 6 февраля и 14 марта того же года. Применяя учетную ставку 10% годовых, банк удержал комиссионные в размере 1000 руб. Определить номинальную стоимость векселей, если номинальная стоимость второго векселя в 2 раза больше, чем номинальная стоимость первого векселя.
Решение
Обозначим номинальную стоимость первого векселя через F, тогда номинальная стоимость второго векселя составит 2∙F.
По таблице порядковых дней в году определим, что первый вексель учтен за 36 дней до срока погашения, а второй вексель учтен за 72 дней до срока погашения.
По формуле (2.5) величина дисконта для первого векселя равна
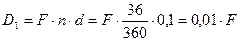
По формуле (2.5 ) величина дисконта для второго векселя равна
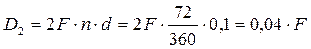
Учитывая, что комиссионные банка за учет двух векселей составили 1000 руб., запишем:
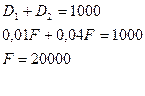
Номинальная стоимость первого векселя составит 20 тыс. руб., номинальная стоимость второго векселя составит 40 тыс. руб.
