Погашение основного долга равными долями

Пусть есть задолженность размером D, выданная на n лет под ставку простых процентов g. По условиям контракта погашение основного долга D должно осуществляться ежегодно равными долями D/n (рис. 9.3), а ежегодно начисляемые на текущую задолженность проценты I уплачиваются единым платежом в конце срока.

График задолженности заемщика по основному долгу будет иметь ступенчатый вид (рис. 9.4) и представлять собой последовательность со значениями:

D, (D – D/n), (D – 2D/n),… ..., D ´ (1 – (k – 1)/n),… ..., D ´ (1 – (n – 2)/n), D ´ (1 – (n – 1)/n). (9.5)

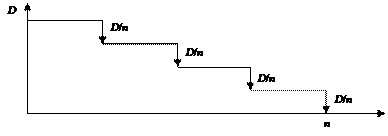Рис. 9.3

Рис. 9.4

Величина «простых» процентов I, начисленных за весь срок ссуды будет равна сумме процентов, начисленных на периодах времени, где база начисления процентов не изменяется (см. Лекцию 1), т.е. будет определяться следующим выражением:

I = g ´ [D + (D – D/n) + ... …+ D ´ (1 – (n – 2)/n) + D ´ (1 – (n – 1)/n). (9.6)

Таким образом, теперь известны все значения, по которым можно составить график погашения задолженности, отвечающий условиям предоставления ссуды (табл. 9.1).

Таблица 9.1

Выплаты по:	1 год	2 год	3 год	n = 4 год
– основному долгу	D/n	D/n	D/n	D/n
– процентам				I
Итоговые платежи	D/n	D/n	D/n	I + D/n

Изменим условие выплаты процентов по задолженности. Будем считать, что проценты должны выплачиваться ежегодно. Таблица выплат, определяющая график платежей будет иметь вид (табл. 9.2):

Таблица 9.2

Выплаты по	1 год	2 год	3 год	n = 4 год
– основному долгу	D/n	D/n	D/n	D/n
– процентам	g ´ D	g ´ (D – D/n)	g ´ (D – 2D/n)	G ´ D ´ (1 – (n– 1)/n)
– итоговым платежам	D/n + g ´ D	D/n + g ´ ´ (D – D/n)	D/n + g ´ ´ (D – 2D/n)	D/n + g ´ D ´ ´ (1 – (n – 1)/n)

Пусть в исходной задаче условием предоставления ссуды предусмотрен льготный период k = 2 года, когда платежи по погашению основного долга отсутствуют, а проценты выплачиваются ежегодно. График задолженности по основному долгу изменится (первые два года первоначальная задолженность неизменна) соответственно неизменна и база начисления процентов в льготном периоде, а после его прошествия база начисления процентов изменяется согласно произведенным выплатам в погашение основного долга. С учетом этих изменений платежи по погашению задолженности будут определяться данными из табл. 9.3.

Таблица 9.3

Выплаты по	1 год	k = 2 год	3 год	n = 4 год
– основному долгу			D/(n – k)	D/(n – k)
– процентам	g ´ D	g ´ D	g ´ (D – D/(n – k))	g ´ D ´ (1 – (n – k – 1)/(n – k))
– итоговым платежам	g ´ D	g ´ D	D/(n – k)+ + g ´ (D – D/(n – k))	D/(n – k) + g ´ D ´ ´ (1 – (n – k–1)/(n – k))

Рассмотрим случай, когда в условиях исходной задачи (задолженность размером D, выдана на n лет под ставку g, погашение основного долга D – осуществляется ежегодно равными долями D/n, а ежегодно начисляемые на текущую задолженность проценты I уплачиваются единым платежом в конце срока) ставка g, по которой начисляются проценты за предоставление ссуды, является сложной. График задолженности по основному долгу останется прежним рис. 9.4. Однако величина процентов, уплачиваемых в конце срока, будет определяться по правилу начисления по сложной ставке, то есть с учетом процентов, начисленных в предыдущие периоды. Рассмотрим последовательно начисление процентов по сложной ставке для каждого года. Величина процентов, начисленных за первый год по сложной ставке g, будет равна I₁ = g ´ D. Во втором год величина «тела» основного долга уменьшится за счет первой выплаты D/n и будет равна D-D/n. При этом, согласно правилам начисления сложных процентов база начисления процентов по сложной ставке g должна увеличится на величину процентов I₁ = g ´ D, начисленных в первый год. То есть ее величина будет равна D – (D/n) + I₁. Следовательно, проценты, начисленные за второй год, будут равны I₂ = g ´ [D – (D/n) + I₁]. В произвольный k-й год база начисления сложных процентов будет состоять из k-го значения задолженности по «телу» долга, т.е. D – (k – 1) ´ (D/n) и процентов I_k-1, начисленных за все предыдущие (k – 1) лет

I_k-1 = g ´ [D – (k – 2) ´ (D/n) + I₁ + I₂ + I₃+… ... + I_k-2].

Завершая рассмотрение первого способа амортизации долга заметим, что основным свойством является требование одинаковости платежей в погашение основного долга, а способы начисления и время выплаты процентов по задолженности при этом могут быть различными и отличаться большим разнообразием.