Номинальная и эффективная ставки
Величину годовой процентной ставки r часто называют номинальной ставкой в отличие от процентной ставки за период r t/T или 1/m.
Для сравнения эффективности предложений различных банков по кредитным операциям их пересчитывают к эффективной процентной ставке 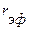 , обеспечивающей ту же доходность, но при начислении процентов один раз в году. Сравнивая (1.6) с
, обеспечивающей ту же доходность, но при начислении процентов один раз в году. Сравнивая (1.6) с
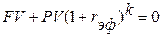 ,
,
получим 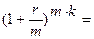
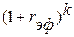 ,
,
| |
откуда 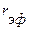 =
= 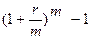 (1.7)
(1.7)
|
Замена в договоре номинальной ставки r при m - разовом начислении процентов на эффективную 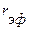 не изменяет финансовых обязательств участвующих сторон. Обе ставки эквивалентны в финансовом отношении. Вообще разные по величине номинальные ставки являются эквивалентными, если соответствующие им эффективные ставки имеют одну и ту же величину.
не изменяет финансовых обязательств участвующих сторон. Обе ставки эквивалентны в финансовом отношении. Вообще разные по величине номинальные ставки являются эквивалентными, если соответствующие им эффективные ставки имеют одну и ту же величину.
При подготовке контрактов может возникнуть необходимость в определении r по заданным значениям 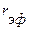 и m. Из (1.7) находим
и m. Из (1.7) находим
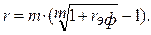 (1.8)
(1.8)
НАЧИСЛЕНИЕ НАЛОГОВ И ПРОЦЕНТЫ
Во многих странах проценты облагаются налогом. Очевидно, что налог на проценты уменьшает наращенную сумму и реальную процентную ставку банка.
Пусть процентная ставка банка r, ставка налога на проценты н, начальная сумма банковского вклада PV, задан срок размещения вклада.
Простые проценты
Наращенная сумма вклада: FV= PV (1+ 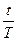 r),где FV и PV взяты по абсолютной величине.
r),где FV и PV взяты по абсолютной величине.
Проценты: I= FV-PV= PV 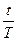 r
r
Проценты после уплаты налога: Iн=I.·(1- н)= PV· 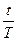 ·r·(1- н)
·r·(1- н)
Наращенная сумма после уплаты налога:
FV=PV+Iн= PV·[1+ 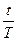 ·r·(1- н)]. (1.18)
·r·(1- н)]. (1.18)
Сложные проценты
Наращенная сумма вклада: 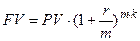 .
.
Проценты: I= FV-PV= 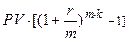 .
.
Проценты после уплаты налога: Iн=I·(1- н)= 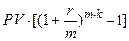 ·(1- н).
·(1- н).
Наращенная сумма после уплаты налога
FV=PV+Iн= 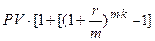 ·(1- н)], откуда
·(1- н)], откуда
| |
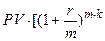 ·(1-н)+н] (1.19)
·(1-н)+н] (1.19)  |
ПРОЦЕНТЫ И ИНФЛЯЦИЯ
Основные понятия
Инфляция – это обесценивание денег, обусловленное чрезмерным увеличением выпущенной в обращение массы бумажных денег и безналичных выплат по сравнению с реальным предложением платных товаров и услуг.
Проявляется инфляция в росте цен на товары. На одни товары цены могут расти, на другие – уменьшаться, но если наблюдается устойчивая тенденция массового повышения цен, то это уже инфляция.
Изменение цен на товары и услуги определяется при помощи индекса цен. Индекс цен численно равен отношению цен на товары, услуги или работы в один период времени к ценам этих же товаров, услуг или работ в другой период времени. Вводят понятие агрегатного индекса цен. Агрегатный индекс цен численно равен отношению цены группы товаров (услуг) за данный период к цене той же группы в базисном периоде. Индекс цен на потребительские и промышленные товары регулярно публикуется. Процентное изменение индекса потребительских цен называется уровнем инфляции.
Пусть S - некоторая сумма денег, имеющаяся у человека в данный момент; St - сумма денег через некоторое время t , покупательная способность которой равна S . Вследствие инфляции St >S и St=S+DS, где DS - некоторая сумма денег, которая добавляется к S для сохранения стоимости годовой "потребительской корзины".
Основными показателями инфляции являются
1. средний годовой уровень инфляции t= (St - S )/S = DS/S
2. годовой индекс инфляции IN= St/S=1+t
Коэффициент падения покупательной способности денег определяется как величина, обратная индексу цен. В США за базисный год принят1967 г. Индекс цен в 1967 году считается за 100%. Индекс цен в 1985 г. равен 322,2%, то есть цены за это время выросли более, чем в 3 раза. Коэффициент падения покупательной способности денег за 1985 г. равен 1/3,222*100%=31,04%. Таким образом, реальная покупательная способность денег равна 31,04% от уровня 1967 года.
Индекс потребительских цен определяется по стоимости "потребительской корзины". Она определяется для трудоспособного мужчины на месяц: хлеба черного - 7 кг 20 г, белого - 3 кг 60 г, муки пшеничной - 540 г, макаронных изделий - 580 г, крупы - 630 г, картофеля - 15 кг, капусты - 2 кг 480 г, яблок - 1 кг 670 г, говядины - 1 кг, свинины - 1 кг 580 г, колбасных изделий -580 г, молока - 10 литров, масла - 500 г, яиц -26 штук, сахара - 2 кг 130 г, чая - 80 г, соли - 830 г.
В России стоимость "потребительской корзины" фиксируется к уровню сентября 1977 года.
Годовой индекс инфляции показывает, во сколько раз возрастает цена "потребительской корзины" за год. При инфляции потребители ускоренно стараются материализовать деньги в товары, что в некоторой степени стимулирует производство, способствует более быстрому обороту денег и развитию экономики. Поэтому в последнее время инфляции не приписывают исключительно деструктивных качеств, так как развитие без инфляции приводит к накоплению денег и оттоку их из производства.
Учет инфляции
Простые проценты
Определим годовую процентную ставку rt, которая бы обеспечила прибыль от наращения по годовой ставке r и покрывала потери от инфляции. Пусть без инфляции будущая сумма
FV = PV (1+ 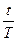 r). (1.20)
r). (1.20)
Наращенная сумма с учетом инфляции, имеющая ту же покупательную способность, что и без инфляции
FVt = PV·(1+ 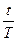 rt). (1.21)
rt). (1.21)
Естественно, что FVt больше FV,
FVt = FV·(1+ 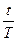 t). (1.22)
t). (1.22)
Из (1.20)-(1.22) получаем
FVt = PV·(1+ 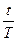 rt)= PV (1+
rt)= PV (1+ 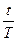 r) (1+
r) (1+ 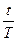 t) (1.23)
t) (1.23)
| |
rt=r+t+ 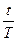 r×t (1.24)
r×t (1.24)
Коэффициент наращения с учетом инфляции
Кt=(1+ 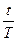 r) (1+
r) (1+ 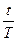 t). (1.25)
t). (1.25)
Он должен быть больше, чем без инфляции К=(1+ 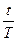 r).
r).
Пусть клиент делает вклад в размере PV в условиях инфляции с годовым уровнем t. Банк обеспечивает ставку rt . Какова реальная годовая процентная ставка прибыли r?
| |
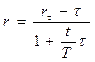 (1.26)
(1.26)
Следовательно, реальная покупательная стоимость будущего вклада составит
|
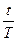
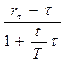 ). (1.27)
). (1.27)
| |||
 | |||
пришлось бы вернуть
| ||
 |
