Задача №3. Определить средний ежемесячный пробег автомашины по данным, представленным в таблице 3.

Таблица 3 – Исходные данные для расчетов

Ежемесячный пробег (тыс. км.)	Число автомашин
от о до 5,0 от 5,0 до 7,0 от 7,0 до 8,0 от 8,0 и более

Решение:

Проведем расчеты, используя формулу среднеарифметической взвешенной. Взвешенная средняя арифметическая – равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков). Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Расчет ведется по формуле (6):

х_ср = (х₁ × f₁ + x₂ × f₂ +…+ x_n × f_n) / (f₁ + f₂ +…+ f_n) = (x × f) /f, (6)

где х – значения вариант,

f – значение весов каждой варианты (частоты).

На первоначальном этапе расчетов определяем середины интервалов, т.е. условные значения варианты каждой интервальной группы.

Для второй и третей групп их определяют по формуле средней арифметической простой:

(5,0 + 7,0) / 2 = 6 тыс. км. (середина интервала второй группы).

(7,0 + 8,0) / 2 = 7,5 тыс. км. (середина интервала третьей группы).

При вычислении середины интервала для первой группы, исходим из предположения, что величина интервала этой группы равна величине интервала следующей (второй) группы, т.е. 7,0 – 5,0 = 2 тыс. км. В таком случае начальное значение интервала первой группы составит 5,0 – 2,0 = 3,0 тыс. км. Следовательно, середина интервала для первой группы составляет:

(3,0 + 5,0) / 2 = 4 тыс. км. (середина интервала первой группы).

При вычислении середины интервала для последней группы исходим из предположения, что она равна величине интервала в предыдущей (третей) группе, а именно, 8,0 – 7,0 = 1,0 тыс. км. Тогда конечное значение интервала последней группы равно 8,0 + 1,0 = 9,0 тыс. км. Следовательно, середина интервала для последней группы составляет:

(8,0 + 9,0) / 2 = 8,5 тыс. км (середина интервала четвертой группы).

Результаты расчетов сведем в таблицу 4.

Таблица 4 – Показатели среднего размера ежемесячного пробега автомашин

Группы машин по размеру их ежемесячного пробега, тыс. км	Середина интервала, тыс. км	Число автомашин
До 5,0
5,0-7,0
7,0-8,0	7,5
8,0 и более	8,5

Средний ежемесячный пробег автомашины по формуле (6) составит:

х_ср = (4 × 40 + 6 × 80 + 7,5 × 130 + 8,5 × 50) / (40 + 80 + 130 + 50) =

= 2040 / 300 = 6,8 тыс. км.

Средний ежемесячный размер пробега автомашин составит 6,8 тыс. км.

Задача №4. Определить среднюю численность работников парикмахерской за месяц, если:

с 1 по 7 число работало 7 человек;

с 8 по 12 – 9 человек;

с 13 по 18 – 5 человек;

с 19 по 27 – 6 человек;

с 28 по 31 – 10 человек.

Решение:

Формула расчета среднесписочной численности работников предприятия за месяц выглядит следующим образом (7):

ССЧ = Сумма человеко-дней за месяц / Количество дней в месяце. (7)

Определим количество дней в каждом временном интервале месяца:

с 1 по 7 число – 7 дней;

с 8 по 12 – 5 дней;

с 13 по 18 – 6 дней;

с 19 по 27 – 9 дней;

с 28 по 31 – 4 дня.

Итого – 31 день.

По формуле (7) средняя численность работников парикмахерской за месяц составит:

СЧЧ = (7 × 7 + 5 × 9 + 6 × 5 + 9 × 6 + 4 × 10) / 31 = 218 / 31 = 7 чел.

Таким образом, средняя численность работников парикмахерской за месяц составила 7 человек.

Задача №5. Известны следующие данные о реализации фруктов предприятиями розничной торговли округа (таблица 5).

Таблица 5 – Данные о реализации фруктов предприятиями розничной торговли округа

Товар	Цена за 1 кг, руб.	Товарооборот, тыс. руб.
июль (р0)	август (р1)	июль (q0)	август (q1)
Яблоки			143,5	167,1
Груши			38,9	45,0

Рассчитайте сводные индексы:

а) товарооборота;

б) цен;

в) физического объема реализации. Определите абсолютную ве­личину экономии покупателей от снижения цен.

Решение:

Сводные индексы позволяют обобщить показатели по нескольким видам товаров.

а) Сводный индекс товарооборота показывает, во сколько раз возросла (уменьшилась) стоимость товаров, или сколько процентов составил рост (снижение) стоимости товаров в текущем периоде по сравнению с базисным. Сводный индекс товарооборота рассчитывается по формуле (8):

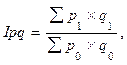(8)

где р₁, р₀ – цена единицы товара в отчетном и базисном периодах.

q₁, q₀ – физические объемы продажи товара в отчетном и базисном периодах.

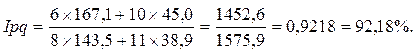
Стоимость товаров в августе по сравнению с июлем снизилась на 7,82% (92,18 – 100).

б) Сводный индекс цен показывает, во сколько раз изменилась стоимость товаров в результате изменения цен, и рассчитывается по формуле 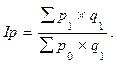(9):

(9)

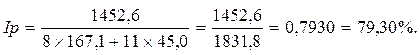
За счет изменения цен товарооборот в августе по отношению к июлю сократился на 20,70% (79,30 – 100).

Величина абсолютной экономии покупателей от снижения цен составила:

ПЦ = 1452,6 – 1831,8 = –379,2 тыс. руб. (экономия)

в) Сводный индекс физического объема реализации показывает во сколько раз изменилась стоимость продукции в результате изменения объема ее реализации. Индекс рассчитывается по формуле 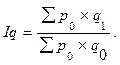(10):

(10)

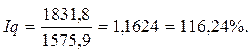
В результате увеличения физического объема реализации товарооборот в августе по сравнению с июлем увеличился на 16,24%.

Таким образом, за период июль-август товарооборот сократился на 7,82%. Данное снижение было вызвано увеличением физического объема продаж, за счет чего товарооборот увеличился на 16,24%. В то же время снижение цен на товары способствовало недополучению товарооборота на 20,70%. За счет снижения цен покупателями получена абсолютная экономия в сумме 379,2 тыс. руб.