Наращение по сложным процентам
Александрова И.А.
Кошкин В. Л.
ФИНАНСОВАЯ МАТЕМАТИКА
РУКОВОДСТВО ПО РЕШЕНИЮ ЗАДАЧ
Владимир 2008
ББК 22.11 я 73
Александрова И.А., Кошкин В.Л. Финансовая математика: Руководство по решению задач: - Владимир: Владимирский государственный гуманитарный университет, 2008 г. – 63 с.
Методическая разработка предназначено для студентов Владимирского государственного гуманитарного университета, представляет собой ряд многовариантных задач по финансовой математике, рекомендации по решению, примеры с решениями по каждому разделу.
| Составители: | к. ф.-м. наук, доцент Александрова И.А. к.геол.-мин.наук, доцент Кошкин В.Л. |
| Ответственный за выпуск: | к. ф.-м. наук, доцент Игонин В.А. |
| Рецензент: | к.ф.-м.наук, доцент Бурков В.Д. |
Печатается по решению редакционно – издательского совета Владимирского государственного гуманитарного университета.
ISBN 5-87-846-271-0
© Владимирский государственный гуманитарный университет, 2008
Оглавление:
| Введение | |
| 1. Простые проценты | |
| 1.1. Простая процентная ставка | |
| 1.2. Простая учетная ставка | |
| 2. Сложные проценты | |
| 2.1. Наращение по сложным процентам | |
| 2.2. Начисление сложных процентов при дробном количестве лет | |
| 2.3. Номинальная процентная ставка. Начисление процентов несколько раз в году | |
| 2.4. Начисление процентов несколько раз в году при дробном количестве периодов начисления | |
| 2.5. Непрерывное начисление процентов | |
| 2.6. Эффективная годовая процентная ставка | |
| 2.7. Расчет срока кредита и процентных ставок | |
| 3. Потоки платежей | |
| 3.1. Формулы наращенной суммы | |
| 3.2. Формулы современной величины | |
| 3.3. План погашения кредита | |
| 4. Инфляция | |
| 4.1. Понятие инфляции | |
| 4.2. Простая процентная ставка с учетом инфляции | |
| 4.3. Простая учетная ставка с учетом инфляции | |
| 4.4. Сложная процентная ставка с учетом инфляции | |
| 5. Приложение | |
| ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ | |
| 7. Литература |
Введение
Данное пособие предлагает систематизированное изложение основных понятий методов финансовых вычислений.
В пособии рассматриваются основные понятия, которыми оперируют в практической деятельности, такие как процент, ставка процента, учетная ставка, современная (текущая) стоимость платежей и т.д., методы наращения и дисконтирования платежей, принципы, лежащие в основе финансовых вычислений, современная практика расчетов.
В настоящее учебное пособие вошли также основы количественного анализа потоков платежей, в частности, - финансовых рент (аннуитетов). Потоки денежных платежей часто встречаются в практике. Например, регулярные взносы для формирования какого-либо фонда (инвестиционного, страхового, пенсионного, для погашения долга), периодическая уплата процентов, доходы по облигациям и ценным бумагам, выплата пенсий, поступление доходов от коммерческой или предпринимательской деятельности, налоговые платежи и т.д. Такие методы имеют важное значение в практике финансовых расчетов и позволяют определить как обобщающие характеристики рент (например, сумму, текущую стоимость), так и отдельные их параметры.
Материал пособия имеет общий характер и является базой для ряда дисциплин. Он может быть применен в расчетах любых финансовых операций: в финансовом менеджменте, в страховом деле, в анализе инвестиционных проектов, расчете кредитных и коммерческих операций, эффективности предпринимательской деятельности и т.д.
Простые проценты
1.1. Простая процентная ставка.
Проценты называются простыми, если за базу их начисления берется только первоначальная сумма.
Пример 1.1. Банк начисляет на вклад 10000 руб. 20% годовых по ставке простых процентов. Найти сумму на счете через 1 год, 2 года, 3 года, …, n лет.
Решение:
Через 1 год на счете будет денег на 20% больше: 10000·(1+0,20)=12000 (руб.);
через 2 года на счете будет: 10000·(1+0,20)+2000=14000 (руб.);
через 3 года на счете будет: 10000·(1+0,20)+4000=16000 (руб.).
Эти данные можно записать следующим образом:
| 1 год – 12000 руб. = 10000·(1+1·0,20) руб. |
| 2 года – 14000 руб. = 10000·(1+2·0,20) руб. |
| 3 года – 16000 руб. = 10000·(1+3·0,20) руб. |
| - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - |
| n лет – сумма на счете = 10000·(1+n·0,20) руб. |
Формула для вычисления простой процентной ставки имеет вид:
| S = P·(1 + n·i), | (1.1) |
Где
S – сумма на счете (наращенная сумма);
P – первоначальная сумма;
n – срок пользования кредитом, в годах;
i – простая процентная ставка.
Если раскрыть скобки формула приобретает вид:
| S = P + P·n·i = P + I, | (1.2) |
Где
I = P·n·i – процентные деньги (Interest).
Наращенная сумма всегда равна первоначальной сумме плюс процентные деньги.
Пример 1.2. Кредит 20 000 руб. выдан на 6 месяцев под 24% годовых, начисляемых по простой процентной ставке. Вычислите возвращаемую сумму.
| Дано: | Решение: |
| P = 20 000 руб. n = 0,5 лет i = 24% = 0,24 | S = P·(1 + n·i) = 20 000·(1 + 0,5·0,24) = 22 400 (руб.) |
| S = ? | Ответ: 22 400 руб. |
Обычно простая процентная ставка используется для случаев n<1 (краткосрочные кредиты).
Если срок пользования кредитом задается двумя календарными датами, день выдачи и день погашения, то формула приобретает вид:
| (1.3) |
где
∂ – срок кредита в днях (день выдачи и день погашения кредита считается за один день).
К – количество дней в году.
Пример 1.3. Кредит 20 000 руб. выдан 17 февраля 2000 г. под 30% годовых, начисляемых по простой процентной ставке. Найти возвращаемую сумму, если день погашения кредита 20 декабря 2000 г.
Решение по формуле (1.3) возможно с применением 3х методик, каждая из которых дает различный результат.
1) «Германская методика».
В каждом месяце 30 дней, а в году 360 дней (30·12 = 360). Подсчет дней кредита производится по следующей схеме:
13 дней + март + апрель + май + июнь + июль + август + сентябрь +
+ октябрь + ноябрь + 20 дней = (13 + 9·30 + 20) дней =303 дня.
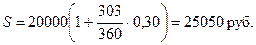К = 360 дней.
Данная методика считает приближенное значение дней пользования кредитом, поэтому говорят о вычислении «обычных процентов» (Ordinary Interest). Применяется в Германии, Дании, Швеции.
2) «Английская методика».
Дни считаются точно по календарной или специальной таблице (см. приложение 1)
17 февраля – 48 день года
20 декабря – 355 день года (год високосный)
 |
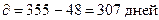К = 366 дней (год високосный)
 |
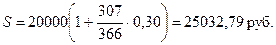Подсчеты дней точные, поэтому говорят о вычислении точного процента (Exact Interest). Применяется в Англии, США, Португалии и др. странах.
3) «Французская методика»
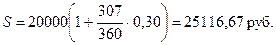Дни считаются как в английской методике, а количество дней в году по германской, т.е. К = 360 дней.
Применяется во Франции, Швейцарии, Испании, Югославии и др. странах.
Так как разные методики дают различные результаты, то при заключении сделок необходимо оговаривать, по какой методике производится расчет. Очевидно, что самая выгодная для кредитора – "Французская методика".
1.2. Простая учетная ставка.
Используется в том случае, когда за базу начисления процентов берется наращенная сумма (S). Обозначается буквой d, широко применяется в финансовых расчетах, например, при оформлении векселей.
Вексель – письменное долговое обязательство строго установленной формы, выдаваемое заемщиком (векселедателем) кредитору (векселедержателю) и предоставляющее последнему бесспорное право требовать с заемщика уплаты к определенному сроку (день погашения векселя) определенной суммы денег, указанной в векселе (номинальной стоимости векселя).
Вексель имеет следующие особенности:
1) абстрактность, т.е. отсутствия каких – либо объяснений по поводу возникновения долга;
2) бесспорность, т.е. обязательность оплаты в точном соответствии с данным векселем;
3) обращаемость, т.е. вексель посредством передаточной надписи может обращаться среди неограниченного количества клиентов.
Вексель можно купить (продать) в любом финансовом учреждении до срока, указанного на нем, но по цене ниже номинальной. В таких случаях говорят, что вексель реализован с дисконтом.
Дисконт (Д) – это разница между номинальной стоимостью векселя (S) и суммой (Р), полученной владельцем векселя в финансовом учреждении при его учете.
Для одного года: S – P = D = S·d
Для n лет: S – P = S·n·d
Отсюда: P = S·(1 – n·d),
где
n – срок между днем погашения и днем учета в годах.
Более удобная формула выглядит следующим образом:
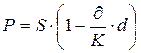 | (1.4) |
Пример 1.4 Владелец векселя номинальной стоимостью 20 000 руб. со сроком погашения 27 декабря 2000 г. собирается реализовать его в банке 20 октября 2000 года. Банк согласен учесть вексель с дисконтом 30%. Вычислить сумму, которую получит в банке владелец векселя.
| Дано: | Решение: |
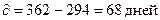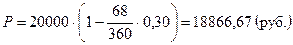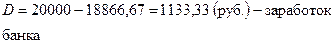   S = 20 000 руб. 20 окт. (294) – день учета векселя 27 дек. (362) – день погашения векселя d = 30% = 0,30 K = 360 дней | |
| P = ? D = ? | Ответ: Владелец векселя получит в банке 20 октября 2000 г. – 18 866,67 рублей; Банк получит от векселедателя 20 000 рублей 27 декабря 2000 г.; Дисконт 1133,33 рублей. |
Пример 1.5 Магазин 14 сентября оптом получает от предпринимателя партию товара общей стоимостью 200 000 рублей на следующих условиях: 40% стоимости оплачивается сразу, а остальное после реализации товара 5 декабря того же года. На какую сумму должен магазин выписать вексель, чтобы предприниматель не потерпел убытков, если банк учитывает векселя по простой процентной ставке 30% годовых.
Предварительное решение: 14 сентября предприниматель получит от магазина – 0,4·200 000 руб. = 80 000 рублей, остальные 120 000 рублей – кредит под 30% годовых начисляемых по простой учетной ставке.
| Дано: | Решение: |
| P = 120 000 руб. 14 сентября – 257 день года 5 декабря – 339 день года d = 0,30 K = 360 дней | |
| P = ? | Ответ: магазин 14 сентября платит предпринимателю 80000 рублей и выписывает вексель на сумму 128801,43 рубля. Предприниматель по векселю стоимостью 128801,43 рубля 14 сентября получает 120000 рублей, т.е. за партию предприниматель получает сразу 80000 рублей в магазине и 120000 рублей в банке. Банк получает 5 декабря дисконт 128801,43–120000 = 8801,43 руб. |
Сложные проценты
Сложные проценты используется в финансово – кредитных операциях, где проценты не выплачиваются сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называют капитализацией процентов.
Наращение по сложным процентам.
Пример 2.1. Банк начисляет на вклад 10000 рублей 20% годовых по ставке сложных процентов. Найти сумму на счете через 1 год, 2 года, 3 года, …, n лет.
Решение:
Через 1 год на счете будет денег на 20% больше: 10000·(1+0,20)=12000 (руб.);
через 2 года на счете будет 12000·(1+0,20) = 10000·(1+0,20)2 = 14400 (руб.);
через 3 года на счете будет 14400·(1+0,20) = 10000·(1+0,20)3 = 17280 (руб.):
Отсюда формула для начисления ставки сложных процентов имеет вид:
| S = P·(1 +i)n, | (2.1) |
Где
S – сумма на счете (наращенная сумма);
P – первоначальная сумма;
n – срок пользования кредитом, в годах;
i – ставка сложных процентов.