Принятие решений в условиях неопределенности
Полная (безнадежная) неопределенность связана с отсутствием информации о вероятностях состояний среды. В этих случаях для определения оптимальных решений используют ряд критериев, выбор каждого из которых зависит от характера решаемой задачи, поставленных целей и ограничений, а также от склонности к риску лица, принимающего решение.
1. Критерий максимакса – М. С его помощью определяется стратегия, максимизирующая максимальные выигрыши для каждого варианта обстановки. Это критерий крайнего оптимизма. Наилучшим признается решение, при котором достигается максимальный выигрыш:
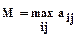(4)
2. Максиминный критерий Вальда (максимин) – W. В соответствии с ним выбирается лучший результат из всех неудачных. Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай. Она ориентирует предпринимателя на слишком осторожную линию поведения. Такая стратегия приемлема тогда, когда предприниматель не столько заинтересован в крупном успехе, сколько стремится избежать неожидаемых проигрышей, и требуется гарантия, чтобы выигрыш в любых условиях оказывался не меньше, чем наибольший из возможных в худших условиях. Оптимальным решением будет то, для которого выигрыш окажется максимальным из всех минимальных при различных вариантах условий:
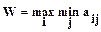(5)
3. Минимаксный критерий Сэвиджа (минимакс) – S. Этот критерий также относится к разряду осторожных. В отличие от критерия Вальда, критерий Сэвиджа минимизирует возможные потери (риски). Он используется тогда, когда требуется в любых условиях избежать большого риска. В соответствии с этим критерием предпочтительным будет решение, для которого потери, максимальные при различных вариантах условий, окажутся минимальными:
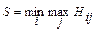(6)
В качестве исходных данных здесь выступают потери (Нij), соответствующие каждой паре сочетаний решений Рi и условий обстановки Оj (таблица рисков).
4. Критерий пессимизма – оптимизма Гурвица – G. Используется тогда, когда требуется остановиться между линией поведения в расчете на худшее (крайним пессимизмом) и линией поведения в расчете на лучшее (безудержным оптимизмом). Согласно этому критерию предпочтение отдается решению, для которого окажется максимальным показатель:
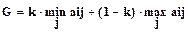(7)
где k – коэффициент пессимизма (0 £ k £ 1); аij – выигрыш, соответствующий i – тому решению при j - том варианте обстановки.
При k = 0 критерий Гурвица совпадает с максимаксным критерием (ориентация на предельный риск, т.к. большой выигрыш, как правило, сопряжен с большим риском), а при k = 1 – с критерием Вальда (ориентация на осторожное поведение).
Применительно к матрице рисков критерий Гурвица имеет вид:
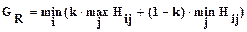(8)
При k=0 выбор стратегии осуществляется по условию наименьшего из всех возможных рисков (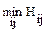 
), при k=1 – по минимаксному критерию Сэвиджа. Самой надежной признается стратегия, которая является оптимальной по большинству из рассмотренных критериев.
5. Принцип недостаточного обоснования Лапласа – используется в случае, если можно предположить, что вероятности всех вариантов обстановки равные. Выбор решения производится по минимуму средневзвешенного показателя риска (формула 3).
В случае, когда по принятому критерию рекомендуется использовать несколько стратегий, выбор между ними может осуществляться по дополнительному критерию, например, на основе среднеквадратического отклонения от средних выигрышей при каждой стратегии.
Задача 2. По данным задачи 1 найти наилучшие стратегии по критериям максимакса, Вальда, Сэвиджа, Гурвица (в зависимости от величины коэффициента пессимизма). Значения критерия Гурвица рассчитать в таблице 4.
Таблица 4 - Значения критерия Гурвица при различных
Коэффициентах пессимизма
| Варианты решений (Рi) | Значение критерия Гурвица | ||||
| k=0,00 | k=0,25 | k=0,50 | k=0,75 | k=1,00 | |
| Р1 | |||||
| Р2 | |||||
| Р3 | |||||
| Р4 | |||||
| Оптимальное решение |
Задача 3. По данным задачи 1 выбрать оптимальную стратегию Р, которая обеспечивает наименьший показатель риска R, если считается, что вероятности каждого варианта обстановки равные (при n=3 вероятность каждого варианта составляет 0,33).
Задача 4. Найти наилучшие стратегии по критериям максимакса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующих данных о возможных выигрышах (табл. 5).
Таблица 5 - Эффективность решений
| Варианты решений (Рi) | Величина выигрышей (аij) в зависимости от вероятных условий обстановки (Оj) | |||||
| О1 | О2 | О3 | О4 | О5 | О6 | |
| Р1 | -33 | -80 | ||||
| Р2 | -40 | |||||
| Р3 | -10 | |||||
| Р4 | -90 | -60 |
Задача 5. Данные, характеризующие эффективность принимаемых решений в условиях полной неопределенности, приведены в таблице 6.
Таблица 6 - Эффективность решений
| Варианты решений (Рi) | Величина выигрышей (аij) в зависимости от вероятных условий обстановки (Оj) | |||
| О1 | О2 | О3 | О4 | |
| Р1 | -2 | |||
| Р2 | -1 | |||
| Р3 | -4 | |||
| Р4 | -1 | |||
| Р5 | -2 |
Требуется проанализировать оптимальные стратегии, используя критерии пессимизма-оптимизма Гурвица применительно к матрице выигрышей и матрице рисков при коэффициенте пессимизма k=0; 0,5; 1; при этом выделить критерии максимакса, Вальда и Сэвиджа; установить, какую роль играет стратегия при k = 0,5.
Задача 6. Предприятие имеет несколько возможных каналов сбыта продукции. Спрос на неё может колебаться. Неопределенность колебаний спроса определяется устойчивостью связей предприятия с покупателями. Общий объем продажи продукции составляет 19730 тыс.руб. В том числе:
а) по каналам с устойчивыми связями по сбыту на ряд лет – в среднем 4900 тыс.руб.(низка зависимость от изменения рыночной конъюнктуры);
б) по каналам с устойчивыми связями, но не на длительный срок – 5000 тыс.руб. (средняя зависимость от изменения конъюнктуры рынка);
в) обеспеченный только разовыми закупками – 5030 тыс.руб. (зависимость от изменения конъюнктуры рынка высокая);
г) объем продукции, покупатель на которую не определен – 4800 тыс.руб. (зависимость от изменения конъюнктуры абсолютная).
Вероятны 4 варианта состояния спроса на продукцию (Оj): О1 – в объеме 4900 тыс.руб.; О2 – 9900 тыс.руб.; О3 – 14930 тыс.руб. и О4 – 19730 тыс.руб. При этом возможны 3 стратегии производства продукции (Рi): Р1 – в объеме 9900 тыс.руб.; Р2 – 14930 тыс.руб.; Р3 – 19730 тыс.руб.
В зависимости от изменения рыночной конъюнктуры в связи с имеющимися возможностями сбыта рассчитаны варианты среднегодовой прибыли (убытка) от продажи – аij (табл. 7). Требуется выбрать оптимальный объем производства продукции на основе критериев Вальда, Сэвиджа, Гурвица.
Таблица 7 – Анализ стратегии производства продукции при
неопределенной конъюнктуре рынка, тыс.руб.
| Стратегия вероятного объема производства (Рi) | Величина прибыли (аij) в зависимости от вероятных колебаний спроса (Оj) | Минимум прибыли (ai= min aij) | Максимин (Wi= max ai) | Максимум прибыли (bi= max aij) | |||
| 4900 О1 | 9900 О2 | 14930 О3 | 19730 О4 | ||||
| -10 | |||||||
| -200 | |||||||
| bj= max aij | х | х | х |
Методические указания к задаче 6
1. Определить максиминную стратегию (по принципу наибольшего гарантированного результата на основе критерия Вальда – W). Максиминная оценка по критерию Вальда является единственной абсолютной надежной при принятии решений в условиях неопределенности. В графе 6 таблицы 7 указать по каждой стратегии минимальные результаты, в графе 7 – наилучший из всех наихудших результатов.
Аналогичный анализ целесообразно провести для второй стороны состояния «природы» – соотношения спроса и стратегии производства. Для этого нужно выявить возможный наихудший исход (минимальный размер прибыли) из всех наилучших (максимальных) исходов действия по каждой стратегий: в графе 8 таблицы 7 указать максимальные из возможных результатов для каждой стратегии производства, из них выбрать минимальный. При наихудшем исходе из всех наилучших по каждой стратегии состояние спроса и предложения дает возможность выиграть (получить прибыль) не более выбранной величины. В последней строке таблицы 7 указать максимальные из возможных результатов по каждому состоянию спроса.
2. Чтобы оценить, насколько то или иное состояние спроса влияет на исход, нужно определить возможные потери прибыли при всех вариантах соотношения спроса и стратегии производства. Потери прибыли (Нij), характеризующие величину риска при вводе стратегии Рi и состоянии спроса Оj, определяются как разность между максимально возможным результатом при данном состоянии спроса Оj (см. последнюю строку таблицы 7) и результатом при каждой стратегии производства, возможной для данного состояния спроса (Нij=bj-aij). Потери прибыли рассчитать в таблице 8. На основе полученных данных определить минимаксную стратегию (по принципу минимальной величины риска в самой неблагоприятной ситуации на основе минимаксного критерия Сэвиджа – S).
Таблица 8 - Анализ потерь прибыли (риска) при различных
соотношениях спроса и стратегии производства, тыс.руб.
| Стратегия производства (Рi) | Величина потерь прибыли (Нij) при различных вариантах состояния спроса и стратегии производства | Максимальные потери (hi=maxHij) | Минимакс (Si=minhi) и оптимальная стратегия | |||
| 4900 О1 | 9900 О2 | О3 | О4 | |||
| 9900 (Р1) | ||||||
| 14930 (Р2) | ||||||
| 19730 (Р3) |
3.Определить оптимальную стратегию производства в соответствии с критерием Гурвица – G. Степень оптимизма в критерии Гурвица принять равной 0,8 (придерживаясь пессимистической оценки).
Задания для самостоятельной работы
Задача 7. Предприятие продает в течение недели 11,12 или 13 тысяч пакетов молока. Затраты на производство 1 тыс. пакетов – 5,6 тыс.руб., а прибыль от её продажи – 3,5 тыс.руб. Если продукция не продана в течение недели, она портится и уничтожается. В этом случае предприятие несет потери в размере затрат на производство (5,6 тыс.руб. на 1 тыс. пакетов). Вероятности продать 11,12 и 13 тыс. пакетов в течение недели равны соответственно 0,45; 0,35; 0,2. Какое количество продукции следует производить?