Тема 5. Выборочное наблюдение
1.

а. 
@б. σ2
в.∆
г.∆2
д. 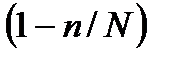
е. (N-1)
2.

а. 
б. σ2
в.∆
@г.∆2
д. 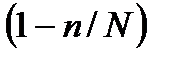
е. (N-1)
3.

а. 
@б. σ2
в.∆
г.∆2
д. 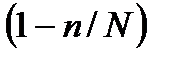
е. (N-1)
4. Репрезентативность результатов выборочного наблюдения зависит от ... .
@ а. вариации признака и объема выборки
б.определения границ объекта исследования
в. времени проведения наблюдения
г.продолжительности проведения наблюдения
5.
а. наличии высокого уровня вариации признака
б.изучении качественных характеристик явлений
@в.малой выборке
г.уточнении данных сплошного наблюдения
6. Средняя ошибка случайной повторной выборки ... , если ее объем увеличить в 4 раза.
@а. уменьшится в 2 раза
б. увеличится в 4 раза
в.уменьшится в 4 раза
г. не изменится
7.
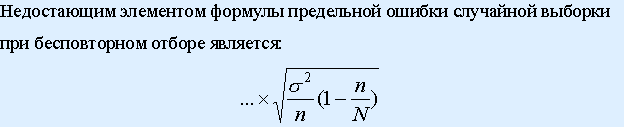
@а.t
б.t2
в.n2
г.n
д.N
е. 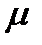
8.Средняя ошибка выборки 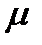 для средней величины характеризует:
для средней величины характеризует:
а. вариацию признака;
б. тесноту связи между двумя факторами;
@в. среднюю величину всех возможных расхождений выборочной и генеральной средней;
г. Среднее значение признака;
д. темп роста;
9. Под выборочным наблюдением понимают:
а. сплошное наблюдение всех единиц совокупности
б. несплошное наблюдение части единиц совокупности
@в. несплошное наблюдение части единиц совокупности, отобранных случайным способом
г. наблюдение за единицами совокупности в определенные моменты времени
д. обследование наиболее крупных единиц изучаемой совокупности
10.Недостающим элементом в формуле дисперсии доли для генеральной совокупности является 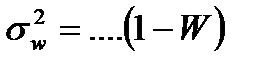
а. р
б. m
в. M
@г. W
11. Пропорция отбора в выборочную совокупность при механической выборке определяется:
@а. соотношением объемов выборочной и генеральной совокупностей;
б. уровнем вероятности;
в. методом отбора.
12.Способ собственно-случайного отбора в выборочную совокупность заключается в отборе из генеральной совокупности:
а. каждой десятой единицы совокупности;
@б. без какой либо системности;
в. в зависимости от уровня вероятности;
13. Необходимая численность серийной выборки при бесповторном отборе определяется по формуле:
а. 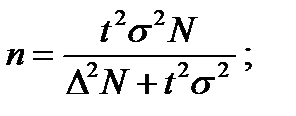
б. 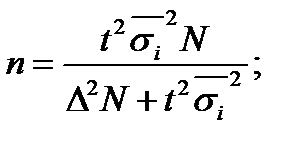
@в. 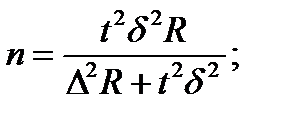
14.Для оценки результатов малой выборки пользуются:
а. критерием Фишера;
@б. критерием Стьюдента;
в. ничем не пользуются;
15. Недостающим элементов в формуле предельной ошибки выборки для доли при бесповторном отборе является: 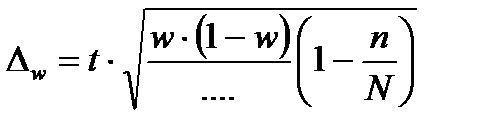
@а. n;
б. N;
в. W;
г. σ;
16.Для получения предельной ошибки выборки необходимо умножить среднюю ошибку выборки на:
@а)коэффициент доверия;
б) численность выборочной совокупности;
в) численность генеральной совокупности.
17.По формуле 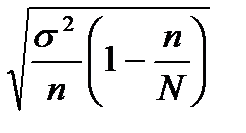 определяется ошибка выборки:
определяется ошибка выборки:
а) средняя повторная;
@б) средняя бесповторная;
в) предельная повторная;
г) предельная бесповторная.
18.При случайном бесповторном отборе средняя ошибка выборки определяется по формуле:
а) 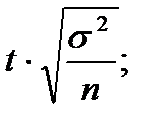
@б) 
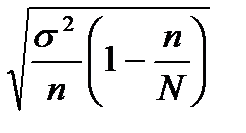 ;
;
в) 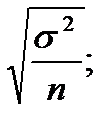
г) 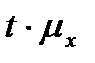
19.Выборка называется малой, если ее объем составляет менее:
а)40 единиц;
@б)30 единиц;
в) 100 единиц;
г)150 единиц;
20.Выборка заключающаяся в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора называется:
а) типической;
@б) механической;
в) случайной повторной.
21Для использования выборочной совокупности для дальнейшего анализа развития социально-экономического явления необходимо, чтобы разница между средним значением генеральной совокупности и средним значением выборочной совокупности была не более ошибки выборки:
а) средней;
б) индивидуальной;
@в)предельной;
г) генеральной.
22.При увеличении численности собственно-случайной повторной выборки в 16 раз, допустимая ошибка выборки…
А. увеличится в 4 раза;
Б. уменьшится в 16 раз;
@В. Уменьшится в 4 раза;
г. Увеличится в 2 раза;
