Имитационное моделирование Монте-Карло

Метод имитационного моделирования Монте-Карло создает дополнительную возможность при оценке риска за счет того, что делает возможным создание случайных сценариев. Применение анализа риска использует богатство информации, будь она в форме объективных данных или оценок экспертов, для количественного описания неопределенности, существующей в отношении основных переменных проекта и для обоснованных расчетов возможного воздействия неопределенности на эффективность инвестиционного проекта. Результат анализа риска выражается не каким-либо единственным значением ЧДД, а в виде вероятностного распределения всех возможных значений этого показателя. Следовательно, потенциальный инвестор с помощью метода Монте-Карло будет обеспечен полным набором данных, характеризующих риск проекта. На этой основе он сможет принять взвешенное решение о предоставлении средств.

В общем случае имитационное моделирование Монте-Карло - это процедура, с помощью которой математическая модель определения какого-либо финансового показателя (в нашем случае ЧДД) подвергается ряду имитационных прогонов с помощью компьютера. В ходе процесса имитации строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами. Процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Результаты имитации собираются и анализируются статистически, с тем чтобы оценить меру риска.

Процесс анализа риска может быть разбит на следующие стадии.

Прогнозная модель Подготовка модели, способной прогнозировать расчет эффективности проекта

Þ

Распределение вероятности (шаг 1) Определение вероятностного закона распределения случайных переменных

Þ

Распределение вероятности (шаг 2) Установление границ диапазона значений переменных

Þ

Þ

Условия корреляции Установление отношений коррелированных переменных

Þ

Имитационные прогоны Генерирование случайных сценариев, основанных на наборе допущений

Þ

Анализ результатов Статистический анализ результатов имитации

Рис. 9.2. Процесс анализа риска

Первая стадия в процессе анализа риска - это создание прогнозной модели. Такая модель определяет математические отношения между числовыми переменными, которые относятся к прогнозу выбранного финансового показателя. В качестве базовой модели для анализа инвестиционного риска обычно используется модель расчета показателя ЧДД

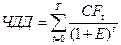
Использование этой формулы в анализе риска сопряжено с некоторыми трудностями. Они заключаются в том, что при генерировании случайных чисел годовой денежный поток выступает как некое случайное число, подчиняющееся определенному закону распределения. В действительности же это совокупный показатель, включающий множество компонент, рассмотренных в предыдущих публикациях. Этот совокупный показатель изменяется не сам по себе, а с учетом изменения объема продаж. То есть ясно, что он коррелирован с объемом. Поэтому необходимо тщательно изучить эту корреляцию для максимального приближения к реальности.

Общая прогнозная модель имитируется следующим образом. Генерируется достаточно большой объем случайных сценариев, каждый из которых соответствует определенным значениям денежных потоков. Сгенерированные сценарии собираются вместе и производится их статистическая обработка для установления доли сценариев, которые соответствуют отрицательному значению ЧДД. Отношение таких сценариев к общему количеству сценариев дает оценку риска инвестиций.

Распределения вероятностей переменных модели (денежных потоков) диктуют возможность выбора величин из определенных диапазонов. Такие распределения представляют собой математические инструменты, с помощью которых придается вес всем возможным результатам. Этим контролируется случайный выбор значений для каждой переменной в ходе моделирования.

Необходимость применения распределения вероятностей обусловлена попытками прогнозирования будущих событий. При обычном анализе инвестиций используется один тип распределения вероятности для всех переменных, включенных в модель анализа. Такой тип называют детерминированным распределением вероятности, и он придает всю вероятность одному значению. При оценке имеющихся данных аналитик ограничен выбором единственного из множества возможных результатов или расчетом сводного показателя. Затем аналитик должен принять, что выбранное значение обязательно реализуется, то есть он придает выбранному наиболее обоснованным образом показателю с единственным значением вероятность, равную 1. Поскольку такое распределение вероятности имеет единственный результат, итог аналитической модели можно определить на основании всего одного расчета (или одного прогона модели).

В анализе рисков используется информация, содержащаяся в распределении вероятности с множественными значениями. Именно использование множественных значений вместо детерминированных распределений вероятности и отличает имитационное моделирование от традиционного подхода.

Определение случайных переменных и придание им соответствующего распределения вероятности является необходимым условием проведения анализа рисков. Успешно завершив эти этапы, можно перейти к стадии моделирования. Однако непосредственный переход к моделированию будет возможен только в том случае, если будет установлена корреляция в системе случайных переменных, включенных в модель. Под корреляцией понимается случайная зависимость между переменными, которая не носит строго определенного характера, например зависимость между ценой реализации товара и объемом продаж.

Наличие в модели анализа коррелированных переменных может привести к серьёзным искажениям результатов анализа риска, если эта корреляция не учитывается. Фактически наличие корреляции ограничивает случайный выбор отдельных значений для коррелированных переменных. Две коррелированные переменные моделируются так, что при случайном выборе одной из них другая выбирается не свободно, а в диапазоне значений, который управляется смоделированным значением первой переменной.

Хотя очень редко можно объективно определить точные характеристики корреляции случайных переменных в модели анализа, на практике имеется возможность установить направление таких связей и предполагаемую силу корреляции. Для этого применяют методы регрессионного анализа. В результате этого анализа рассчитывается коэффициент корреляции, который может принимать значения от -1 до 1.

Стадия "прогонов модели" является той частью процесса анализа риска, на которой всю рутинную работу выполняет компьютер. После того, как все допущения тщательно обоснованы, остается только последовательно просчитывать модель (каждый пересчет является одним "прогоном") до тех пор, пока будет получено достаточно значений для принятия решения (например. более 1000).

В ходе моделирования значения переменных выбираются случайно в границах заданных диапазонов и в соответствии с распределениями вероятностей и условиями корреляций. Для каждого набора таких переменных вычисляется значение показателя эффективности проекта. Все полученные значения сохраняются для последующей статистической обработки.

Окончательной стадией анализа рисков является обработка и интерпретация результатов, полученных на стадии прогонов модели. Каждый прогон представляет вероятность события, равную

p = 100 : n,

где p - вероятность единичного прогона, %,

n - размер выборки.

Например, если количество случайных прогонов равно 5000, то вероятность одного прогона составляет

p = 100 : 5000 = 0,02 %.

В качестве меры риска в инвестиционном проектировании целесообразно использовать вероятность получения отрицательного значения ЧДД. Эта вероятность оценивается на основе статистических результатов имитационного моделирования как произведение количества результатов с отрицательным значением и вероятности единичного прогона. Например, если из 5000 прогонов отрицательные значения ЧДД окажутся в 3454 случаях, то мера риска составит 69.1%.

Контрольные вопросы

1. Что обычно понимается под неопределенностью и риском?

2. Каковы возможности количественного описания риска?

3. Какие основные виды рисков присущи инвестиционному проекту?

4. Как описать неопределенность с помощью наиболее простого способа?

5. Почему неопределенная форма задания данных требует у менеджера меньшей ответственности?

6. Какие Вам известны подходы к анализу рисков в процессе инвестиционного проектирования?

7. В чем сущность анализа чувствительности?

8. Сформулируйте основные достоинства и недостатки анализа чувствительности при анализе рисков инвестиционного проекта.

9. В чем смысл анализа сценариев при анализе рисков инвестиционных проектов?

10. Какие сценарии называются пессимистичными и оптимистичными?

11. На основе каких сценариев (пессимистичных или оптимистичных) инвестор предпочитает принимать решение?

12. В чем сущность имитационного моделирования при анализе рисков?

13. В каком смысле имитационное моделирование может рассматриваться как обобщение метода анализа сценариев?

14. Что используется в качестве механизма генерации прогонов в методе имитационного моделирования?

15. Какова общая расчетная схема метода имитационного моделирования?

16. Объясните смысл понятия “корреляции” применительно к анализу рисков. Почему необходимо учитывать корреляцию?

17. Какую количественную меру риска можно оценить с помощью имитационного моделирования?

18. Можно ли вручную произвести имитационное моделирование реального проекта?

ЛИТЕРАТУРА

1. Балабанов И.Т. Риск-менеджмент. – М.: Финансы и статистика, 1996.

2. Банковское дело и финансирование инвестиций / Под ред. Н. Брука. Т. 1, Т. 2. – Вашингтон: Институт экономического развития Всемирного Банка, 1996.

3. Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов: Теория и практика: Учеб.-практ. пособие. – М.: Дело, 2001.

4. Воропаев Ю.Н. Оценка риска аудита и бизнеса // Бухгалтерский учет. – 1996, №6.

5. Деева А.И. Инвестиции: Учебное пособие. – М.: Издательство «Экзамен», 2004.

6. Золотогоров В.Г. Инвестиционное проектирование: Учебное пособие. – Мн.: ИП «Экоперспектива», 1998.

7. Кейн Э. Экономическая статистика и эконометрия. Введение в количественный экономический анализ / Пер. с англ. – М.: Статистика, 1977.

8. Колтынюк Б.А. Инвестиции: Учебник. – СПб.: Издательство Михайлова В.А., 2003. – 848с.

9. Лимитовский М.А. Инвестиции на развивающихся рынках. – М.: ООО Издательско-Консалтинговая Компания «ДеКА», 2002.

10. Липсиц И.В., Коссов В.В. Инвестиционный проект. – М.: БЕК, 1996.

11. Мелкумов Я.С. Организация и финансирование инвестиций: Учебное пособие. – М.: ИНФРА-М, 2000.

12. Методические рекомендации по оценке эффективности инвестиционных проектов: (Вторая редакция)/ М-во экон. РФ, М-во фин. РФ, ГК по ст-ву, архит. и жил. политике; рук. авт. кол.: Коссов В.В., Лившиц В.Н., Шахназаров А.Г. – М.: ОАО «НПО «Изд-во Экономика», 2000. – 421 с.

13. Орлова Е.Р. Инвестиции: Курс лекций. 2-е изд., доп. и пер. – М.: Омега-Л, 2003.

14. Проект и его жизненный цикл. Т. 1, Т. 2. – Вашингтон: Институт экономического развития Всемирного Банка, 1994.

15. Разработка и анализ проектов. Т. 1, Т. 2. – Вашингтон: Институт экономического развития Всемирного Банка, 1994.

16. Риски в современном бизнесе / П.Г. Грабовый, С.Н. Петрова, С.И. Полтавцев и др. – М.: Аланс, 1994.

17. Руководство по циклу проекта. - Вашингтон: Институт экономического развития Всемирного Банка, 1994.

18. Сердюкова И.Д. Методы анализа финансовых рисков // Бухгалтерский учет. – 1996, №6.

19. Скрибнер Л., Пюри Г. Анализ безубыточности / Банковское дело и финансирование инвестиций. Под ред. Н. Брука, Ч 1, Т 1. – Вашингтон, Институт экономического развития Всемирного Банка, 1996.

20. Шарп У., Александер Г., Бейли Д. Инвестиции. – М.: Инфра-М, 1997.

Сергей Владимирович Горбунов,

Алексей Николаевич Никифоров

Инвестиционный

Анализ

Е издание

Учебное пособие

Редактор

Н.А. Воронова

Подписано в печать Формат 60×90 1/16. Бумага газетная.

Печать трафаретная. Уч.-изд. л. 5,8. Усл. печ. л. 6,2.

Тираж 500 экз. Заказ №_____

Государственное образовательное учреждение высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»,

603950, Н.Новгород, Ильинская, 65

Полиграфцентр ННГАСУ, 603950, Н.Новгород, Ильинская, 65