Дисконтный срок окупаемости инвестиционного проекта

Дисконтный срок окупаемости проекта k определяется тоже из условия равенства всех полученных доходов всем произведенным расходам, приведенных к начальному моменту инвестиций, то есть из уравнения (3.4).

В этом случае процентная ставка банка r считается заданной. К сожалению, уравнение (3.4) также является нелинейным относительно k. В Excel нет финансовой функции, определяющей срок окупаемости инвестиции с не равными поступлениями. Определить k из (3.4) можно методом перебора. Поясним метод на примере 3.1.

Для этого воспользуемся функцией ВНДОХ Excel и построим зависимость внутренней нормы доходности IRR от срока инвестиционного проекта.

Рис.3.1

На этом же графике отложим r процентную ставку банка. Абсцисса точки пересечения графиков и дает срок окупаемости проекта. Из графика видно, что срок окупаемости ресторанного бизнеса при ставке банка r =12% порядка 4,2 года

Индекс доходности инвестиционного проекта

Его называют также показателем рентабельности проекта. Он равен отношению всех денежных поступлений к суммарным инвестиционным расходам, приведенным к начальному моменту сделки. Обозначим его U.

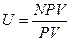. (3.6)

Естественно, что он должен быть больше единицы. Чем выше U, тем привлекательнее проект.

В примере 3.1 при r=12%

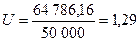
- довольно высокий показатель.

Сравнение эффективности двух инвестиционных проектов при платежах m раз в году

В разделах 3.2.1 - 3.2.7 мы рассмотрели пример, когда начисление процентов и платежи происходили регулярно в конце каждого года в течение k лет.

Пусть теперь поступления (или выплаты) и начисления процентов происходят регулярно постнумерандо m раз в году.

В этом случае число периодов n=m·k, а процентная ставка за период составит r/m. Все формулы переписываются таким образом.

1) Наращенная сумма поступлений

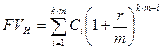. (3.7)

2) Сумма, наращенная на первоначальный капитал

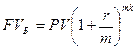. (3.8)

3) Сумма дохода (долга), приведенная к началу сделки,

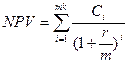. (3.9)

В соответствии с формулой (3.3) величину приведенного дохода NPV можно вычислить с помощью финансовой функции НПЗ. В формуле НПЗ в качестве аргумента ставка нужно подставлять величину r/m, а число членов значения возрастает до m·k.

4) Внутренняя норма доходности IRR сделки является корнем уравнения

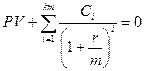. (3.10)

Величину IRR/m в соответствии с (3.5) можно рассчитать также с помощью функции ВНДОХ. В формуле ВНДОХ с числом значений произойдет та же метаморфоза, что и в функции НПЗ; в качестве предположения нужно подставлять величину r/m.

5) Срок окупаемости n_ок=k_ок´m инвестиционного проекта станет корнем того же уравнения (3.10) при известной ставке банка r.

6) Индекс доходности проекта

,

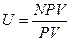где NPV определяется из (3.9).

Пример 3.2

Фирма имеет возможность вложить 100 млн. руб. в один из двух инвестиционных проектов А и Б сроком на 4 года.

Проект А предполагает поступление дохода каждые полгода постнумерандо. Проект Б - ежегодные поступления в конце каждого года. Исходные данные приведены в таблице 3.2

.

Таблица 3.2

	А	B	C	D
	Год	Проект А млн. руб.	Год	Проект Б млн. руб.
		-100		-100
	0,5
	1,5
	2,5
	3,5
	Доход
	IRR=	22,72%		20,02%

В строке 11 показаны суммарные поступления для обоих проектов. Для второго проекта они на 10 млн. рублей больше, однако, по ним нельзя судить о привлекательности проекта.

В строке 12 рассчитана внутренняя норма доходности обоих проектов. Напомним, что функция ВНДОХ определяет IRR за период. Поэтому, чтобы определить годовую норму доходности первого проекта, ее нужно удвоить.

Итак, в ячейке В12 введена формула = 2*ВНДОХ(В3:В11), а в ячейке D12 - финансовая функция = ВНДОХ(D3:D6).

Расчет показывает, что внутренняя норма доходности проекта А выше, чем у проекта Б, следовательно, с этой точки зрения он привлекательнее.

Но не будем делать скоропалительных выводов. Проведем более глубокий анализ. Построим зависимость дисконтированной суммы дохода для обоих проектов от ставки банка r ( Таблица 3.3 и график 3.2).

В ячейку G3 помещаем формулу = НПЗ(F3/2;$B$3:$B$10), и копируем ее в ячейки G4:G19. В ячейку Н3 вводим функцию = НПЗ(F3;$D$3:$D$6) и ее копируем в ячейки Н4:Н19.

Таблица 3.3

	F	G	H
1		Дисконтированная сумма дохода
	Ставка	Проект А млн. руб.	Проект Б млн. руб.
	0%	150,00	160,00
	2,5%	142,62	149,78
	5%	135,82	140,54
	7,5%	129,54	132,16
	10%	123,73	124,53
	12,5%	118,34	117,58
	15%	113,34	111,22
	17,5%	108,70	105,39
	20%	104,37	100,04
	22,5%	100,34	95,11
	25%	96,57	90,56
	27,5%	93,05	86,35
	30%	89,75	82,46
	32,5%	86,65	78,84
	35%	83,75	75,48
	37,5%	81,02	72,35
	40%	78,44	69,43

Расчет показывает, что для r < 11,24% предпочтительнее все же вариант Б, его чистый приведенный доход выше. При r>11,24% привлекательнее проект А. Значение r=11,24%, при котором NPV_А = NPV_Б называется точкой Фишера. Точное ее значение можно определить методом Поиск решения.

Для этого в ячейку, например, J3 поместим число 5%, в ячейку K3 – формулу = НПЗ(J3/2;B2:B10), а в ячейку K4 – формулу=НПЗ(J3;B2:B6), вычисляющие приведенный доход по проекту А и Б соответственно.

В ячейку K5 поместим функцию цели:=К3 – К4.

Вызовем: Сервис – Поиск решения. В появившемся окне Поиск решения набираем:

Установить целевую ячейку: $K$5 равной ¤ значению: 0,

изменяя ячейки: J3.

Выполнить.

В ячейке J3 получаем искомое решение IRR=11,24%, при котором NPV в обоих вариантах равны.

В таблицах 3.4 и 3.5 и соответствующих им графиках 3.3 и 3.4 показаны зависимости эффективности проектов А и Б от срока выполнения договора.

Таблица 3.4

Год	Проект А млн. руб.	IRR
	-100
0,5
1,5
		-10,29%
2,5		1,83%
		7,26%
3,5		7,26%
		11,36%

Проект А начинает окупаться примерно через 2,7 года, а проект Б только с 3,3 года. Точку Фишера первый проект проходит через 3,3 года, а второй – через 3,8 года. Динамика индекса доходности в обоих проектах совпадает с динамикой NPV.

Таблица 3.5

Год	Проект Б млн. руб.	IRR
	-100
		-20,00%
		4,70%
		20,02%

Итак, мы видим, что различные критерии не однозначно определяют привлекательность того или иного проекта. Окончательный выбор остается за лицом, принимающим решение (ЛПР).