Построение доверительных интервалов для среднего

Задание 5

Пусть имеется выборка, содержащая числовые значения: 13, 15, 17, 19, 22, 25, 19. Необходимо определить границы 95%-ного доверительного интервала для среднего значения.

Решение

1. В диапазон А1:А7 введите исходный ряд чисел.
2. В ячейке В1 найдите среднее значения исходного диапазона, с помощью функции СРЗНАЧ.
3. В ячейке В2 найдите стандартное отклонение диапазона, с помощью функции СТАНДОТКЛОН.
4. Выделите ячейку В3, вызовите Мастер функций, категория Статистические, функция ДОВЕРИТ. В поле Альфа введите число 0,05, которое означает 95%-й уровень значимости, в поле Станд_откл выделите ячейку В2, в поле Размер введите размер выборки - число 7. Нажмите Ok.
5. В ячейке В3 появится полуширина 95%-ного доверительного интервала для среднего значения выборки. Для нахождения нижней границы доверительного интервала от среднего значения в В1 надо отнять полученное значение в В3, для нахождения верхней границы следует прибавить В1 и В3. В В4 введите формулу =В1-В3 , в В5 - формулу =В1+В3 .

Задание 6

Для данных из задания 5 найти границы 95%-ного доверительного интервала для среднего значения с помощью процедуры Описательная статистика.

Решение

1. В диапазон А1:А7 введите исходный ряд чисел.
2. Выберите в меню Сервис команду Анализ данных, выделите строку Описательная статистика, нажмите Ok.
3. В поле Входной интервал выделите диапазон А1:А7, активируйте переключателем поле Выходной интервал и укажите ячейку В1. В разделе Группировка, установите переключатель по столбцам. Установите флажок в поле Уровень надежности и введите 95, нажмите Ok.
4. В указанном выходном диапазоне получим значение доверительного интервала. Для нахождения нижней границы доверительного интервала от среднего значения надо отнять полученное значение, для нахождения верхней границы – прибавить. Выборочное среднее значение находится обычно одновременно с доверительным интервалом процедурой Описательная статистика,следует толькоустановить флажок в поле Итоговая статистика.

Упражнения

Определите границы 95%-ного доверительного интервала выборки 2, 3, 5, 7, 4, 9, 6, 4, 9, 10, 4, 7, 9. Используйте функцию ДОВЕРИТ и процедуру Описательная статистика.

Анализ двух выборок

Задание 7

Сравнивается количество баллов по тесту у двух групп студентов. Необходимо определить достоверность различия между группами при двух вариантах постановки задачи:

· группы состоят из разных студентов;

· группы состоят из одних и тех же студентов, но первая – до посещения курсов, а вторая – после.

	A	B	C
	1 группа	2 группа
3 д
	0,212244	0,001081

Решение

1. Введите исходные данные.
2. Для выявления достоверности отличий выделите свободную ячейку А8, вызовите Мастер функций, категория Статистические, функция ТТЕСТ, в поле Массив1выделите диапазон данных первой группы А2:А6, в поле Массив2 выделите диапазон данных второй группы В2:В6, в поле Хвосты всегда вводится цифра 2, в поле Тип введите цифру 3. Нажмите Ok. В ячейке А8 появится значение вероятности.
3. Поскольку величина вероятности случайного появления анализируемых данных 0,212244 больше уровня значимости 0,05, то нулевая гипотеза не отвергается. Следовательно различия между выборками могут быть случайными, поэтому на основании применения критерия Стьюдента нельзя сделать вывод о достоверности отличий двух групп студентов по количеству баллов, набранных по тесту.
4. Для решения второго варианта задачи, выделите ячейку В8, вызовите Мастер функций, категория Статистические, функция ТТЕСТ, в поле Массив1выделите диапазон данных первой группы А2:А6, в поле Массив2 выделите диапазон данных второй группы В2:В6, в поле Хвосты всегда вводится цифра 2, в поле Тип введите цифру 1. Нажмите Ok. В ячейке В8 появится значение вероятности.
5. Поскольку величина вероятности случайного появления анализируемых данных 0,001081 меньше уровня значимости 0,05, то нулевая гипотеза отвергается. Следовательно, различия между выборками не случайные и можно сделать вывод о том, что в двух группах студентов выявлены достоверные отличия по количеству набранных баллов, что явилось результатом посещения курсов.

Упражнения

Выявить достоверны ли отличия при сравнении данных реализации турфирмой путевок за периоды до, и после начала рекламной компании. Ниже приведены количества реализованных путевок по месяцам.

	A	B	C
	С рекламой	Без рекламы
3 д

Задание 8

Пусть после окончания двух институтов экономического профиля трудоустроились по специальности из первого институту 90 человек, а из второго 60 (обе группы молодых специалистов включали по 1000 человек). Достоверны ли отличия по успешности трудоустройства?

Решение

1. Принимается нулевая гипотеза, что выборки принадлежат к одной генеральной совокупности.
2. Введите данные в рабочую таблицу: в ячейку А1 – 90, в В1 – 60, в ячейке А2 найдите среднее А1 и В1 с помощью функции СРЗНАЧ, в ячейке В2 – тоже среднее А1 и В1.
3. Выделите ячейку А3, вызовите Мастер функций, категория Статистические, функция ХИ2ТЕСТ, в поле Фактический интервал выделите диапазон А1:В1, в поле Ожидаемый интервал выделите диапазон А2:В2. Нажмите Ok.
4. Поскольку полученное значение вероятности 0,014306 меньше уровня значимости 0,05, то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и выборки считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия хи-квадрат можно сделать вывод о том, что в двух группах выпускников выявлены достоверные отличия по успешности трудоустройства.

Упражнения

В ходе социологического опроса ответы распределились следующим образом:

	Мужчины	Женщины
Да
Нет
Не знаю

Есть ли достоверные отличия в ответах мужчин и женщин?

Задание 9

Для данных из задания 7 определить достоверность различия между группами студентов с помощью процедур пакета Анализ данных.

Решение

Рассмотрим первый случай, когда группы состоят из разных студентов.

1. Введите исходные данные.
2. Поскольку данные не имеют попарного соответствия следует использовать процедуру Двухвыборочный t-тест с различными дисперсиями.Для этого в меню Сервис выберите команду Анализ данных, выделите Двухвыборочный t-тест с различными дисперсиямии нажмите Ok.
3. В поле Интервал переменной1 выделите диапазон А2:А6, в поле Интервал переменной2 выделите В2:В6, установите переключатель в поле Выходной интервал и укажите ячейку А8. Нажмите Ok.
4. В указанном выходном диапазоне появятся результаты процедуры. Величина вероятности случайного появления анализируемых выборок (P(T<=t) двухстороннее) 0,212174 больше уровня значимости 0,05, т.е. различия между выборками могут быть случайными.

Рассмотрим второй случай, когда группы состоят из одних и тех же студентов, но первая – до посещения курсов, а вторая – после.

1. Поскольку данные имеют парное соответствие следует использовать процедуру Парный двухвыборочный t-тест для средних. Выберите эту процедуру через меню Сервис, команда Анализ данных.
2. В поле Интервал переменной1 выделите диапазон А2:А6, в поле Интервал переменной2 выделите В2:В6, установите переключатель в поле Выходной интервал и укажите ячейку D8. Нажмите Ok.
3. В указанном выходном диапазоне появятся результаты процедуры. Величина вероятности случайного появления анализируемых выборок (P(T<=t) двухстороннее) 0,00108 меньше уровня значимости 0,05, т.е. нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и выборки считаются достоверно отличающимися друг от друга.

Упражнения

1. Определите, достоверны ли различия в количестве приобретаемых туристических путевок семейными парами и отдельными туристами.

	Количество приобретаемых путевок
Месяцы
Семейные пары
Отдельные туристы

1. В таблице приведены результаты группы студентов по скоростному чтению до и после специального курса по быстрому чтению. Произошли ли статистически значимые изменения скорости чтения у студентов?

Студент
До курса
После

Получение случайных чисел

Задание 10

1. Введите в ячейку А1 формулу =СЛЧИС(), которая генерирует случайное число в диапазоне от 0 до 1. Нажимайте F9. В ячейке изменяется выводимое число.

2. Введите в ячейку В1 формулу =СЛУЧМЕЖДУ(1;50), которая возвращает случайное целое число, лежащее в указанных границах и скопируйте ее в В2: J20. Нажимайте F9.

Задание 11

1. Постройте следующую таблицу:

	A	B	C	D	E
	Среднее			Среднее
	Стандартное отклонение	0,3		Стандартное отклонение

1. Для получения нормально распределенных случайных величин воспользуйтесь функцией НОРМОБР. В С1 введите формулу =НОРМОБР(СЛЧИС();$В$1;$В$2) и скопируйте ее в блок С2:С20. В ячейках Е1 и Е2 введите формулы для расчета среднего значения и стандартного отклонения С1:С20.
2. Нажимая F9 , посмотрите как в ячейках Е1 и Е2 изменяются значения, но остаются близкими к значениям в ячейках В1 и В2.

Задание 12

Предположим, что вы проводите 10 презентаций в неделю и 20 % из них заканчиваются заключением сделки. Хотелось бы узнать, насколько будет успешным следующий год.

Решение

1. В меню Сервис выберите команду Анализ данных, укажите Генерация случайных чисел и нажмите Ok.
2. В поле Число случайных чисел введите 50 (50 рабочих недель в году). В поле Распределение выберите Биномиальное. В поле Значение p введите 0,2 (20 %) и в поле Число испытаний – 10.
3. Укажите выходной диапазон. Для этого установите флажок в поле Выходной интервал и введите, например, А1. Нажмите Ok.
4. В столбце А получите 50 случайных чисел, среди которых будут несколько нулевых. Это означает, что на этой неделе не будет заключена сделка.

Задание 13

Проводятся курсы по 7 различным предметам: математика, физика, химия, английский язык, информатика, литература, история. Необходимо составить расписание на месяц, так чтобы предметы чередовались в случайном порядке.

Решение

1. Пронумеруйте предметы по порядку: 1 – математика, 2 – физика, 3 – химия, 4 – английский язык, 5 – информатика, 6 – литература и 7 – история. Введите числа 1 – 7 в диапазон А1:А7.
2. Укажем желаемую вероятность появления каждого предмета. Пусть все предметы будут равновероятны (p = 1/7). Введите число 1/7 в диапазон В1:В7. Для этого в ячейку В1 введите формулу =1/7 и скопируйте её в диапазон В2:В7.
3. В меню Сервис выберите команду Анализ данных, укажите Генерация случайных чисел и нажмите Ok.
4. Укажите Число переменных – 1, Число случайных чисел – 30 (количество дней в месяце). В поле Распределение выберите Дискретное.
5. В поле Входной интервал значений и вероятностей введите (мышью) диапазон, содержащий номера предметов и их вероятности – диапазон А1:В7.
6. Установите флажок в поле Выходной диапазон и введите С1. Нажмите Ok.
7. В столбце С получите 30 случайных чисел, например: 3, 1, 5, 7, 7, 1, 3, …, и т.д. Это означает, что в первый день следует проводить курсы по химии, во второй – по математике, в третий – по информатике и т.д.

Упражнения

1. Создать последовательность 1000 нормально распределенных случайных чисел, имеющее среднее значение – 100 и стандартное отклонение – 2.
2. Создать последовательность из 10 действительных случайных чисел, равномерно распределенных в диапазоне от 3 до 7.
3. Составить расписание на месяц для случайной демонстрации на телевидении одного из 4-х рекламных роликов некоторой фирмы. Причем вероятность появления рекламного ролика № 1 должна быть в 2 раза выше, чем остальных рекламных роликов. (Используйте Дискретное распределение).

Корреляционный анализ

Задание 14

Имеются результаты наблюдений реализации путевок двух туристических маршрутов тура А и тура В по месяцам. Необходимо определить, имеется ли взаимосвязь между количеством продаж путевок обоих маршрутов.

	A	B	C
	Месяцы	Тур А	Тур В
	Март
3 д	Апрель
	Май
	Июнь
	Июль
	Август

Решение

1. Введите исходные данные.
2. Выделите свободную ячейку В8, вызовите Мастер функций, категория Статистические, функция КОРРЕЛ, в поле Массив1 выделите диапазон В2:В7, в поле Массив2 выделите диапазон С2:С7, нажмите Ok.
3. В ячейке В8 появится значение коэффициента корреляции 0,98875. Значение коэффициента корреляции больше чем 0,95. Значит, можно говорить о том, что в течение периода наблюдений имелась высокая степень прямой линейной взаимосвязи между количествами проданных путевок обоих маршрутов.

Задание 15

C помощью процедуры Корреляция определить, имеется ли взаимосвязь между годовым уровнем инфляции (%), ставкой рефинансирования (%) и курсом доллара (руб./$), по следующим данным ежегодных наблюдений:

	А	В	С
	Уровень инфляции	Ставка рефинансирования	Курс $
			6,3

Решение

1. Введите исходные данные.
2. Выберите в меню Сервис команду Анализ данных, выделите строку Корреляция, нажмите Ok.
3. В поле Входной интервал выделите диапазон А2:С6, установите переключатель в поле Выходной интервал и укажите ячейку А8. Нажмите Ok.
4. В выходном диапазоне получаем корреляционную матрицу.

	Столбец 1	Столбец 2	Столбец 3
Столбец 1
Столбец 2	0,98934348
Столбец 3	-0,90463239	-0,9151724

1. Таким образом, в результате анализа выявлены зависимости: очень сильная степень линейной взаимосвязи между уровнем инфляции и ставкой рефинансирования (r=0,98934348), сильная степень обратной линейной взаимосвязи между уровнем инфляции и курсом $ (r=-0,90463239). Между курсом $ и ставкой рефинансирования имеется сильная обратная взаимосвязь (r=-0,9151724).

Упражнения

1. Определить, имеется ли взаимосвязь между рождаемостью и смертностью (количество на 1000) человек в Санкт-Петербурге.

Годы	Рождаемость	Смертность
	9,3	12,5
	7,4	13,5
	6,6	17,4
	7,1	17,2
	7,0	15,9
	6,6	14,2

1. Имеются ежемесячные наблюдения за состоянием погоды и посещаемостью музеев и парков. Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.

Число ясных дней	Кол-во посетителей музея	Кол-во посетителей парка

Регрессионный анализ

Задание 16

Дан набор точек: (0,3) , (1,1) , (2,6) , (3,3) , (4,7). Найти коэффициенты а и b прямой линии Y=aX+b , наилучшим образом аппроксимирующей эти данные.

Решение

1. Введите координаты точек в диапазон А2:В6 .

	A	B
	X	Y

1. Для того, чтобы найти коэффициенты а и b, выделите диапазон А7:В7, вызовите Мастер функций, категория Статистические, функция ЛИНЕЙН, в поле Известные значения Y выделите диапазон В2:В6, в поле Известные значения Х выделите диапазон А2:А6, поля Конст и Статистика оставите пустыми и нажмите комбинацию клавиш Ctrl+Shift+Enter.
2. В ячейке А7 получим значение коэффициента а, в ячейке В7 – значение коэффициента b.
3. Искомое уравнение прямой линии будет иметь вид Y=X+2.
4. Для того чтобы вывести полную статистику, выделите блок из 5 строк и 2 столбцов - D2:E6, вызовите Мастер функций, выберите Статистические, ЛИНЕЙН. Первым аргументом укажите блок В2:В6, вторым аргументом – блок А2:А6, в третьем и четвертом поле поставьте 1, нажмите Ctrl+Shift+Enter.
5. Получите таблицу, в которой в D2 записан коэффициент – а; в E2 – коэффициент b; в D3 и E3 – стандартные отклонения для этих коэффициентов; в D4 – коэффициент детерминации R2, чем ближе он к 1, тем лучше регрессионное уравнение описывает зависимость; в E4 – стандартная ошибка для оценки y; в D5 – значение F-статистики; в E5 – количество степеней свободы; в D6 – регрессионная сумма квадратов; в E6 – остаточная сумма квадратов.

Задание 17

Для заданного набора пар значений независимой переменой и функции определить наилучшее линейное приближение в виде прямой с уравнением Y=aX+b и показательное приближение в виде линии с уравнением Y=b·a^X .

Решение

1. В столбец А, начиная с ячейки А1, введите 10 произвольных значений независимой переменой.
2. В столбец В, начиная с В1, введите 10 произвольных значений функции.
3. В диапазоне С1:D1 найдите коэффициенты а и b искомой прямой, с помощью функции ЛИНЕЙН.
4. Чтобы из полученного массива извлечь значения в отдельные ячейки, используйте функцию ИНДЕКС. Для этого выделите ячейку С3, вызовите Мастер функций, категория Ссылки и массивы, функция ИНДЕКС, в поле Массив выделите С1:D1, в поле Номер строки укажите число 1, получите значение коэффициента а.
5. Для извлечения коэффициента b, выделите ячейку D3, выполните действия аналогично предыдущему пункту, только в поле Номер строки укажите число 2.
6. В диапазоне Е1:F1 найдите коэффициенты а и b показательного приближения. Для этого выделите диапазон Е1:F1,вызовите мастер функций, категория Статистические, функция ЛГРФПРИБЛ, в поле Известные значения Y выделите диапазон В1:В10, в поле Известные значения Х выделите диапазон А1:А10, поля Конст и Статистика оставите пустыми и нажмите комбинацию клавиш Ctrl+Shift+Enter.
7. В ячейки Е3 и F3 извлеките коэффициенты а и b с помощью функции ИНДЕКС.

Задание 18

Для данных из задания 16 найти наилучшее линейное приближение с помощью процедуры Регрессия.

Решение

1. Для построения наилучшей прямой другим способом выберите Сервис – Анализ данных – Регрессия, в поле Входной интервал Y укажите диапазон, содержащих значение функции В2:В6, в поле Входной интервал Х укажите диапазон, содержащих значение независимой переменной А2:А6, установите переключатель в поле Выходной интервал и укажите ячейку А10, нажмите Ok.
2. В выходном диапазоне появятся результаты регрессионного анализа. В строке Регрессия в столбце Значимость F находится уровень значимости критерия Фишера, который должен быть меньше чем 0,05, чтобы модель была значима.
3. В строке Y-пересечение находится коэффициент b, в строке Переменная Х1 – коэффициент а, в столбце Р-значение приводится достоверность отличия соответствующих коэффициентов от нуля, если Р>0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная не влияет на зависимую переменную.

Задание 19

Имеются данные спроса на продукции малого предприятия за 9 месяцев. Необходимо спрогнозировать значения продаж за 10, 11 и 12 месяцы.

Месяц
Спрос (тыс.руб.)

Решение

1. В диапазон А2:А10 введите порядковые числа месяцев, в диапазон В2:В10 введите данные продаж.

2. Для нахождении каждой точки на линии регрессии, выделите диапазон С2:С10, вызовите Мастер функций, выберите Статистические, функция ТЕНДЕНЦИЯ.

3. В поле Изв_знач_y укажите блок В2:В10, в поле Изв_знач_х – блок А2:А10, третий и четвертый аргумент опустите. Нажмите Ctrl+Shift+Enter.

4. Для вычисления спроса за 10, 11 и 12 месяцы, введите числа от 10 до 12 в ячейки А11:А13. Выделите С11:С13, введите формулу =ТЕНДЕНЦИЯ(В2:В10; А2:А10; А11:А13), и нажмите Ctrl+Shift+Enter.

Задание 20

После выброса ядовитого вещества его концентрация в водоеме изменялась в соответствии со следующей таблицей:

Время после выброса (час)	Концентрация вещества (мг/л)
	8,0
	2,8
	1,0
	0,3

Необходимо аппроксимировать данные уравнением вида .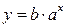

Решение

1. В диапазон А2:А5 введите время после выброса, в диапазон В2:В5 ведите соответствующие концентрации вещества.

2. Выделите диапазон С2:D2 под массив результатов, вызовите Мастер функций, выберите Статистические, функция ЛГРФПРИБЛ.

3. В поле Изв_знач_y укажите блок В2:В5, в поле Изв_знач_х – блок А2:А5, Константа – 1, Стат – 0. Нажмите Ctrl+Shift+Enter .

4. В результате в ячейке С2 получите значение коэффициента а – 0,63, а в ячейке D2 – значение коэффициента b – 11,84.

Таким образом, искомое аппроксимирующее уравнение имеет вид:

.

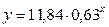5. Построим диаграмму по исходным данным. Вызовите Мастер диаграмм, выберите:

· Тип диаграммы – Точечная, вид – второй с верху, нажмите Далее;

· В поле Диапазон укажите с помощью мыши диапазон данных – В2:В5, установите переключатель Ряды в: столбцах, откройте вкладку Ряд, в поле Значения Х, с помощью мыши укажите диапазон А2:А5,в поле Имя введите – Концентрация, нажмите Далее;

· Введите название диаграммы – Концентрация вещества, название осей Х и Y: Время и Концентрация соответственно, нажмите Готово. Получен график экспериментальных данных (рис 3).

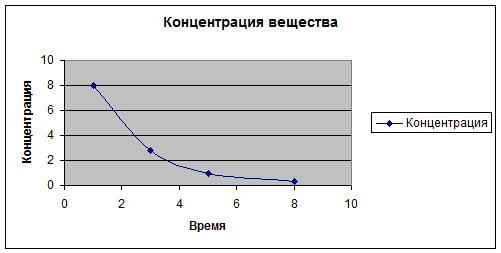
Рис 3.Экспериментальные данные, аппроксимируемые экспоненциальной функцией

Упражнения

1. Имеются данные о цене на нефть X и индексе акций нефтяных компаний Y. Постройте зависимость индекса акций нефтяных компаний от цены на нефть.

	A	B
	X	Y
	17,28
	17,05
	18,30
	18,80
	19,20
	18,50

1. Постройте зависимость жизненной емкости в литрах Y от роста в метрах Х₁ и возраста в годах Х₂ для группы мужчин:

	А	В	С
	Х1	Х2	Y
	1,85		5,4
	1,8		5,7
	1,75		4,8
	1,7		5,1
	1,68		4,5
	1,73		4,8
	1,77		5,1
	1,81		5,6
	1,76		4,7

1. Количество вложенных в производство средств и полученная в результате прибыль соотносится следующим образом:

Х	1,6	2,0	2,5	3,0	4,0	7,0
Y	8,5	9,0	11,0	13,0	22,0	70,0

Необходимо аппроксимировать данные уравнением вида 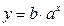и найти неизвестные параметры. Какая будет прибыль, если вложить 10,0 единиц?

1. Постройте зависимость зарплаты от возраста сотрудника отдела по следующим данным:

Возраст
Зарплата