Начисление сложных процентов в условиях налогообложения

В долгосрочных операциях при начислении налога на сложные проценты возможны следующие варианты: налог начисляется за весь срок сразу, т.е. на всю сумму процентов, или последовательно, например в конце каждого года. В первом случае сумма налога равна P[(1 + i)ⁿ - 1]g, а наращенная сумма после выплаты налога

S" = S - (S - P)g = S(1 - g)+ Pg = P[(1 - g)(1+ i)ⁿ + g].(2.38)

Во втором случае сумма налога определяется за каждый истекший год. Очевидно, что она является переменной величиной, так как сумма процентов увеличивается во времени. Соответственно увеличивается и годовая сумма налогов. Сумма налогов за весь срок, очевидно, не зависит от метода начисления.

Налог за год t (обозначим его как G_t)можно найти с помощью следующего рекуррентного выражения:

G_t = I_tg = (S_t - S_t-1)g = P[(1 + i)^t - (1 + i)^t-1]g.

20.Потоки платежей. Классификация потоков. Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производиться через разные интервалы времени.

Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой, или просто рентой, а иногда аннуитетом (annuity) независимо от назначения или происхождения платежей. Например, рентой являются последовательность получения процентов по облигации, платежи по потребительскому кредиту, выплаты в рассрочку страховых премий и т. д. Как видим, во всех приведенных случаях выплаты или получения денег производятся через равные промежутки времени. Использование в финансово-банковской операции условий, предполагающих выплаты в виде финансовой ренты, существенно упрощает количественный их анализ, дает возможность применять стандартные формулы и таблицы значений ряда необходимых для расчетов коэффициентов и быстро выполнять расчеты на калькуляторах.

Рента характеризуется следующими параметрами: член ренты (rent) — размер отдельного платежа, период ренты (rent period, payment period) — временной интервал между двумя последовательными платежами, срок ренты (term) — время от начала первого периода ренты до конца последнего периода, процентная ставка. Размер ставки не всегда прямо оговаривается в условиях финансовой ренты, вместе с тем этот параметр крайне необходим для ее анализа.

При характеристике отдельных видов рент необходимы дополнительные условия и параметры: число платежей в году, способ и частота начислений процентов.

В практике применяют разные по своим условиям ренты. В основу их классификации могут быть положены различные признаки. Рассмотрим некоторые из таких классификаций.

По количеству выплат членов ренты на протяжении года ренты делятся на годовые (выплата раз в году) и р-срочные (р — количество выплат в году). В анализе производственных инвестиционных процессов иногда применяют ренты с периодами, превышающими год. Перечисленные виды рент называют дискретными. В финансовой практике встречаются и с такими последовательностями платежей, которые производятся столь часто, что их практически можно рассматривать как непрерывные.

По количеству начислений процентов на протяжении года различают: ренты с ежегодным начислением, с начислением т раз в году, с непрерывным начислением. Моменты начисления процентов необязательно совпадают с моментами выплат членов ренты. Однако, как будет показано, расчеты заметно упрощаются, если два указанных момента совпадают.

По величине своих членов ренты делятся на постоянные (с одинаковыми платежами) и переменные. Члены переменных рент изменяют свои размеры во времени, следуя какому-либо закону, например арифметической или геометрической прогрессии, либо несистематично (задаются таблицей).

По вероятности выплат ренты делятся на верные (annuity certain) и условные (contingent annuity). Верные ренты подлежат безусловной уплате, например при погашении кредита. Число членов такой ренты заранее известно. В свою очередь выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. К такого рода рентам относятся страховые аннуитеты — различные последовательные платежи в имущественном и личном страховании. Типичным примером страхового аннуитета является пожизненная выплата пенсии.

По количеству членов различают ренты с конечным числом членов, т. е. ограниченные по срокам ренты (их срок заранее оговорен), и бесконечные, или вечные, ренты (perpetuity). С вечной рентой встречаются на практике в ряде долгосрочных операций, когда предполагается, что период функционирования анализируемой системы или срок операции весьма продолжителен и не оговаривается конкретными датами. В качестве вечной ренты логично рассматривать и выплаты процентов по облигационным займам с неограниченными сроками.

По соотношению начала срока ренты и какого-либо момента времени, упреждающего начало ренты (например, начало действия контракта или дата его заключения), ренты делятся на немедленные и отложенные, или отсроченные (deffered annuity).

Очень важным является различие рент по моменту выплат платежей в пределах периода. Если платежи осуществляются в конце периодов, то соответствующие ренты называют обыкновенными, или постнумерандо (ordinary annuity), если же платежи производятся в начале периодов, то их называют пренумерандо (annuity due). Иногда контракты предусматривают платежи или поступления денег в середине периодов.

Приведем пример. Контракт предусматривает периодическое погашение задолженности выплатой в конце каждого полугодия одинаковых погасительных платежей на протяжении фиксированного числа лет. Таким образом, предусматривается постоянная, полугодовая, верная, ограниченная рента постнумерандо. Если первая выплата в счет погашения основной суммы долга производится спустя, скажем, два года после подписания контракта (льготный период), то эта рента является отложенной относительно даты заключения договора.

Обобщающие параметры потоков платежей. В подавляющем числе практических случаев анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости. Наращенная сумма (amount of cash flows) — сумма всех членов потока платежей с начисленными на них к концу срока процентами. Под современной стоимостью потока платежей (present value of cash flows) понимают сумму всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени. (В старой русской финансовой литературе аналогичный по содержанию показатель назывался настоящей ценой платежей.) Конкретный смысл этих характеристик определяется содержанием его членов или их происхождением. Наращенная сумма может представлять собой общую сумму накопленной задолженности к концу срока, итоговый объем инвестиций, накопленный денежный резерв и т. д. В свою очередь современная стоимость характеризует приведенные к началу осуществления проекта инвестиционные затраты, суммарный капитализированный доход или чистую приведенную прибыль от реализации проекта и т. п.

Обобщающие поток платежей характеристики, особенно его современная стоимость, широко применяются в различных финансовых расчетах. Так, без них, например, невозможно разработать план последовательного погашения задолженности, измерить финансовую эффективность проекта, осуществить сравнение или безубыточное изменение условий контрактов, решить многие другие практические задачи. В связи со сказанным основное внимание в данной главе уделено методам расчета наращенных сумм и современных стоимостей постоянных финансовых рент. Однако до этого необходимо обсудить более общие подходы, применяемые при определении названных параметров при анализе нерегулярных потоков платежей.

Прямой метод расчета наращенной суммы и современной стоимости потока платежей. Рассмотрим общую постановку задачи. Допустим, имеется ряд платежей R_t, выплачиваемых спустя время п_t после некоторого начального момента времени, общий срок выплат я лет. Необходимо определить наращенную на конец срока сумму потока платежей. Если проценты начисляются раз в году по сложной ставке i, то, обозначив искомую величину через S,получим по определению:

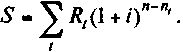(4.1)

Как видим, наращенную сумму в заданных условиях получают методом прямого счета. Современную стоимость такого потока находим прямым счетом — как сумму дисконтированных платежей. Обозначив эту величину как А,получим:

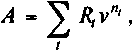(4.2)

где — 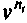дисконтный множитель по ставке i.

Современная стоимость потока платежей представляет собой его обобщающую оценку, приуроченную к некоторому предшествующему моменту времени (у немедленной ренты — к началу срока). Наращенная сумма — это тоже не что иное, как представление всех членов потока в виде одного числа, однако приурочена эта оценка к концу срока. Нетрудно обнаружить, что между величинами А и S существует функциональная зависимость. В самом деле, дисконтировав сумму S спомощью дисконтного множителя vⁿ, получим:

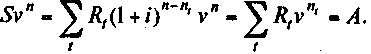
Соответственно, наращивая сумму А по ставке i, получим:

A(1+ i)ⁿ = S.

21.Финансовые ренты и их классификация. Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.

При рассмотрении финансовой ренты используются основные категории:

· член ренты (R) – величина каждого отдельного платежа;

· период ренты (t) – временной интервал между членами ренты;

· срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода;

· процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента.

Поскольку условия финансовых сделок весьма разнообразны, постольку разнообразны и виды потоков платежей. В основе классификации финансовых рент положены различные качественные признаки:

· В зависимости от периода продолжительности ренты выделяют

o годовую ренту, которые представляют собой ежегодные платежи, т.е. период ренты равен 1 году;

o срочную ренту, при которой период ренты может быть как более, так и менее года.

· По числу начислений процентов различают

o ренты с начислением 1 раз в год;

o ренты с начислением mраз в год;

o непрерывное начисление.

· По величине членов ренты могут быть

o постоянные ренты, где величина каждого отдельного платежа постоянна, т.е. рента с равными членами;

o переменные ренты, где величина платежа варьирует, т.е. рента с неравными членами.

· По числу членов ренты они бывают

o с конечным числом членов (огра0000000000000ниченные ренты), когда число членов ренты конечно и заранее известно;

o с бесконечным числом (вечные ренты), когда число ее членов заранее не известно.

· По вероятности выплаты ренты делятся на

o верные ренты, которые подлежат безусловной выплате, т.е. не зависят не от каких условий, например, погашение кредита;

o условные ренты, которые зависят от наступления некоторого случайного события.

· По методу выплаты платежей выделяют

o обычные ренты, которые на практике встречаются чаще всего, – с выплатой платежа в конце периода ренты (постнумерандо);

o ренты, с выплатой в начале периода ренты (пренумерандо).

22.Наращенная сумма обычной годовой ренты. Рассмотрим определение наращенной суммы на примере наиболее простого случая, – годовой постоянной обычной ренты:

где FVA – наращенная сумма ренты;

R – размер члена ренты, т.е. размер очередного платежа;

i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах,

s n;i – коэффициент наращения ренты.

Пример. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение:

Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.

Сумма всех взносов с начисленными процентами будет равна:

Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами (Приложение 4), содержащими коэффициенты наращения ренты:

FVA = R • s5 ; 30 = 500 • 9,0431 = 4'521,55 руб.

Сумма взносов в течение 5 лет составит:

P = n • R = 5 • 500 = 2'500 руб.

Следовательно, сумма начисленных процентов будет равна:

I = FVA - P = 4'521,55 - 2'500 = 2'021,55 руб.

Таким образом, доход владельца счета за 5 лет составит 2'021,55 руб.

Для овладения методами финансовой математики важно не столько запоминание формул, сколько общих принципов расчета.

Для определения наращенной суммы на конец рассматриваемого периода последовательно присоединяются промежуточные результаты наращения к очередному платежу.

Рассмотрим поэтапное решение предыдущего примера:

Расчет наращенной величины аннуитета

Период

Взносы*

Проценты, начисленные за период

Наращенная сумма на конец периода

500,00

-

500,00

500,00

150,00

1150,00

500,00

345,00

1995,00

500,00

598,50

3093,50

500,00

928,05

4521,55

* Взносы поступают в конце периода.

Таким образом, получается такая же сумма, как и по формуле наращения аннуитета.

Однако рассматриваемая формула используется только при начислении процентов один раз в год, но возможны случаи и неоднократного начисления процентов в течение года, тогда используют следующую формулу:

где j – номинальная ставка процентов.

Пример. Рассмотрим предыдущую задачу, изменив условия: проценты начисляются поквартально.

Решение:

В этом случае рента с начислением процентов 4 раза в год, а общее количество начислений составит 20 раз. Отсюда сумма всех взносов с начисленными на них процентами будет равна:

Отсюда сумма начисленных процентов будет равна:

I = FVA - P = 4'840,76 - 2'500,00 = 2'340,76 руб.

Как видим, переход от годового начисления процентов к ежеквартальному начислению заметно увеличил как наращенную сумму, так и сумму процентов.

Бывают случаи, когда рентные платежи вносятся несколько раз в год равными суммами (срочная рента), а начисление процентов производится только раз в году. Тогда наращенная величина ренты будет определяться по формуле:

Также нередки случаи, когда рентные платежи вносятся несколько раз в году и начисление процентов также происходит несколько раз в год, но число рентных платежей не равно числу периодов начисления процентов, т.е. p ? m. Тогда формула по которой можно определить наращенную величину финансовой ренты примет вид:

На практике большее распространение получил поток постнумерандо, поскольку согласно общим принципам учета принято подводить итоги и оценивать финансовый результат операции или иного действия по окончании очередного отчетного периода. Что же касается поступления денежных средств в счет оплаты, то на практике они чаще всего распределены во времени неравномерно и поэтому для удобства все поступления относят к концу периода, что позволяет использовать формализованные алгоритмы оценки.

Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз.

23.Годовая рента, начисление процентов m раз в году. Не будем выводить формулу для этого случая, а заменим в формуле (4.14) дисконтный множитель (1 + i)^-n на эквивалентную величину (1 +j/m)^-mn, соответственно i заменим на (1 +j/m)^m - 1, после чего имеем:

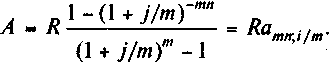
24.Рента p-срочная (m = 1). Если платежи производятся не один, a p раз в году, то коэффициенты приведения находятся так же, как и в случае годовой ренты. Только теперь размер платежа равен R/p, а число членов np. Сумма дисконтированных платежей равна:

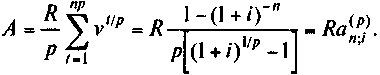
25.Рента p-срочная (p = m). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m. В итоге

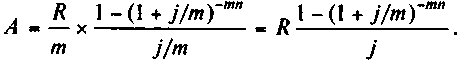(4.18)

Искомый результат можно получить и по формуле (4.14) и при этом воспользоваться таблицей коэффициентов приведения постоянных рент. В этом случае вместо числа лет берется количество периодов ренты, процентная ставка и величина члена ренты определяются соответствующим образом

26.Рента p-срочная (p <> m). Сумма членов соответствующей прогрессии составит

.
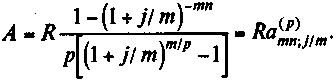