Дисконтирование по сложной процентной ставке

Деньги в рыночной экономике – товар. Любой товар в рыночной экономике должен производить доход. Капитал делится на промышленный, торговый, ссудный. Промышленный капитал распадается на торговый и ссудный. Ссудный капитал это и есть деньги. Ссудный % - доход, который получает тот кто ссужает деньги или предоставляет кредит. Доход может определяться в виде простых и сложных процентов. Обслуживание кредита – доход банка – сумма выплаченных в качестве % денег.

Простые проценты.

Наращивание – процесс увеличения первоначальной суммы. Множитель наращивания – отношение наращенной суммы к первоначальной. Интервал начисления – n. Когда не требуется особая точность (обычные = коммерческие %) принимается год = 360 дней, Точное исчисление % - год = 365(366) дней.

Задача 1. Ссуда в размере P (первоначальная сумма) = 50 млн. руб выдана на n = 0,5 года по простой ставке процентов i = 200% годовых. Определить наращенную сумму S.

S=P(1+in) =50(1+0,5*2)=100 млн. руб

Задача 2. Кредит в размере 10 млн. руб выдан 2.03 по 11.12 под 180% годовых. Год високосный. Определить размер наращенной суммы для различных вариантов а) точный % (365/365)

Б) обыкновенный % с точным числом дней (365/360)

В) обыкновенный % с приближенным числом дней (360/360)

S=P(1+in), Р=10 млн, i=1,8.

А) n=284/366, S=10(1+284*1,8/366)=23,97

Б) n=284/360, S=10(1+284*1,8/360)=24,2

В) n=279/360, S=10(1+279*1,8/360)=23,95

Задача 3.Кредит выдан 10.02.97 с возвратом 20.11.97. Ставка 22% годовых. Определить какую сумму должен забрать в конце срока кредита, если в начале срока получил 6 млн. руб. Расчет по трем вариантам а, б, в.

А) S = 6 (1+283*0,22/365) = 7,019

Б) S = 6 (1+283*0,22/360) = 7,033

В) S = 6 (1+279*0,22/360) = 7,023

Задача 4. Кредит 20 млн. руб. выдан на 3,5 года. Ставка % в первый год – 150%, за каждое последующее полугодие она увеличивается на 10%. Определить коэффициент наращивания и наращенную сумму.

S = 20 (1+1,5+0,5(1,6+1,7+1,8+1,9+2)) = 140 млн.,

Коэф. Наращ. = 140/20 = 7

Дисконтирование.

Определение первоначальной суммы.

Задача 5. Найти первоначальную сумму, которая в итоге даст 3 тыс. руб, 90 дней, банк дает 10% годовых.

P = S /(1 + in) = 3000/(1+0,1*90/365)=2927,8

Коэффициент (множитель) дисконтирования – 1+in. Дисконтирование – процент при введении стоимости будущего времени к современному при помощи множителя дисконтирования. Бывает: математическое и по методу банковского учета (связано с вексельным обращением). Вексель – обязательство через определенное время оплатить стоимость покупки. Вексель обращается как деньги. В конце концов векселедержатель отдает вексель в банк и получает деньги. С суммы векселя банк получает какой-либо доход (дисконт). Банк берет себе - в зависимости от того на сколько раньше погашен вексель и в зависимости от ссудного %.

Задача 6. Через 180 дней после подписания договора должник заплатит 310 тыс руб. Кредит под 16% годовых. Какова первоначальная сумма долга? (Временная база – 365 дней). Чему равен дисконт?

P = S /(1 + in) = 310 000/(1+0,16*180/365) = 287 328

Дисконт S-P = 310 – 287 = 23

Задача 7. Какую сумму получит в банке кредитополучатель, если через 150 дней он должен вернуть 7,5 млн. руб. i=27%, временная база – 365 дней.

P = S /(1 + in) = 7,5/(1+0,27*150/365)=6,75 млн. руб

Учетные ставки

Задача 8. Кредит выдается на 0,5 года по простой учетной ставке 50%. Рассчитать сумму, полученную заемщиком и величину дисконта, полученную банком, если нужно возвратить 2 млн. руб.

P = S (1 - in) = 2(1-0,5*0,5) = 1,5 млн. руб.

Дисконт S-P = 2 - 1,5 = 0,5 млн. руб

Задача 9. Кредит в размере 40 млн. руб выдается по учетной ставке 50% годовых. Определить срок на который предоставляется кредит, если заемщик получает 30 млн. руб.

P = S (1 - in), n = (1-P/S)/i

S>P, n = (1-30/40)/0,5 = 0,5 – полгода

Задача 10.Предполагается внести 1000$ на рублевый депозит. Курс продажи 1500 руб/$, курс покупки – 1820 руб/$ к окончанию срока. Процентная ставка по рублевому счету – 220%, по валютному – 15%. Срок депозита – 3 месяца. Что выгоднее? Каким должен быть конечный курс $ при котором стоит приобретать $?

Перевод в рубли, рублевый счет, перевод в $: 1000*1500 = 1500000 руб, i=220%, n = ¼, S=P(1+in)=1500000*(1+2,2*1/4)=2325000, 2325000/1820 = 1277,47 $

Валютный счет: i = 15%, n = ¼, S=P(1+in)=1000 (1+0,15*1/4)=1037,5$

Перевод в рубли более выгоден.

1037,5 * курс = 2325000, 1$ = 2240,9 руб.

Задача 11. ВВП = 2,6 трлн. Руб. наличные деньги в обращении – 400 млрд. руб. На счетах в банках находится 700 млрд. руб. Срочные и сберегательные вклады – 300 млрд. руб. В ценных бумагах – 100 млрд. руб. определить агрегаты М₀, М₁, М₂, М₃ и скорость обращения денежных средств по методике ЦБ.

М₀=400, М₁=М₀+700=1100, М₂=М₁+300=1400, М₃=М₂+100=1500

Скорость обращения = ВВП / Ден. Масса = 2,6 трлн./ М₂ = 2600/1400 = 1,86.

Погашение ссуды частями. Существует два метода: 1) метод торговца – остаток долга на конец периода определяется как разность между наращенной суммой долга и наращенной суммой накопленных платежей. Остаток долга q = S₂ – S₁ = P (1+in) – R(1+in), R – сумма платежей. 2) актуарный метод – последовательное начисление % на фактическую сумму долга K₁=D₀(1+in)-R, R – промежуточный платеж, D₀ – сумма долга в первом периоде. Разница в процентах.

Сложные проценты.

Задача 12. Какой величины достигнет долг, равный 1 млн руб через N = 5 лет при ставке 15,5% годовых?

S = P(1+i)^N = 1000(1+0,155)⁵ = 2055 руб.

Задача. Определить годовой доход векселя, если вексель номиналом 10 000 руб приобретен по цене 8620 руб. куплен 11.01, погашен 3.05 того же года.

Д= доход/ инвестированный капитал, доход = 10000 – 8620 = 1740, доходность за период = 1740/8260 = 0,21065, годовая доходность = 0,21065*365/112 = 0,68 = 68 %.

Задача . Вексель номиналом 10 000 руб приобретен по цене 8620 руб. куплен 11.01, погашен 3.05 того же года. Определить доход владельца банковского векселя, если он продал бумагу за 30 дней до погашения при действии рыночной ставки 60%.

10000 (1 – 0,6/12) = 9500, доход – 9500-8260=1240.

Задача . Вексель номин. Стоимостью 500 тыс руб был учтен в банке за 90 дней до срока погашения по учетной ставке 16%. Определить дисконтированную величину векселя.

Сумма, выданная банком = сумма векселя (1-ni)

Дисконт в пользу банка = 500*0,16/4 = 20

P_учета=500-20=480

Задача . Долговое обязательство в сумме 2 млн. руб. должно быть погашено через 90 дней с 120% годовых. Владелец обязательства учел его в банке за 15 дней до окончания срока по учетной ставке 135% годовых. Определить полученную при учете сумму.

S =2 000(1+1,2*90/360) = 2600

Д = 2600*1,35*15/365=156 – дисконт в пользу банка

P_уч=2600-156=2444

Задача . Определить доходы банков по учету и переучету векселя суммой 100 тыс. руб, если учет производится КБ за 72 дня до даты погашения при ставке 8%, а переучет ЦБ по ставке 6% за 30 дней до даты погашения.

Учет векселя – перепродажа векселя до срока погашения.

100000(1-0,06*30/365) = 99 500, доход ЦБ = 500,

100000 (1-0,08*72/365) = 98 400, доход КБ 1600 – 500 = 1100.

Задача . Вексель номиналом 30 тыс. со сроком погашения 6.09 учтен 6.06 при 6% годовых. Найти дисконтированную величину векселя.

Р_учет=30000(1-0,06*92/365) = 29546

Задача . Для погашения долга величиной 100 тыс. со сроком погашения 18.04 заемщик выписал своему кредитору векселя: один на сумму 10 тыс руб сроком погашения 25.06, другой на сумму 18 тыс руб со сроком погашения 5.07 и два одинаковых векселя со сроками погашения 18.05 и 3.06. Найти номинальную величину этих двух векселей при 6% годовых.

Х – стоимость векселя.

100000 = 10000 (1 - 0,06 * 68/365) + 20000 (1 - 0,06 * 78/365) + Х (1 -0,06 * 30/365) + Х (1 - 0,06 * 46/365), Х = 35411 руб.

доходность облигации = доход/вложенный капитал

Курс акции = рыночная цена/номинал*100

Задача: Срок ссуды 5 лет. Договорная процентная ставка 12% годовых, маржа 0,5% в первые 2года и 0,75% в оставшиеся. Определить множитель наращивания.

Маржа – доход банка (дилера) – тех субъектов денежного обращения, которые в нем участвуют (или комиссионеров).

Решение: (1+i)^N – множитель наращивания. S=P*(1+i)^N.

(1+i)^N=(1+0,12+0,005)²*(1+0,12+0,0075)³=1,81, где 0,12 - %-ая ставка,

0,005 – маржа за первые 2 года и 0,0075 – маржа за 3,4,5-е годы.

Ответ: (1+i)^N=1,81

Задача: Чем короче период, тем выше доход (в Европе). Процентная ставка 8% начисляется в течении 5 лет поквартально. Определить число периодов и определить множитель.

Решение: 1) 5*4=20, так как в году четыре квартала

2) (1+i)^N=(1+0,08)²⁰=4,66.

Если число периодов в году m ,а годовая ставка y, то y/m называется номинальной ставкой сложных процентов. Номинальная годовая ставка позволяет определить ставки процентов по каждому периоду.

Задача:Какой величины достигнет капитал в 1 млн. долларов через 5 лет, если проценты(%) начисляются поквартально при ставке 15,5% годовых.

Решение: S=P*(1+I/m)^N=1*(1+0,155/4)²⁰=2,14.

Ответ: 2,14

Задача: Первоначальная сумма 2000 рублей(P). Определить наращенную сумму через 5 лет при использовании простых и сложных процентов, если ставка 80% годовых.

Решить при условии что проценты(%) начисляются: а) по полугодиям. б) по квартально.

Решение: S=P*(1+i*n) – простые проценты(%).

S=P*(1+y/m)^N – сложные проценты(%).

S=2*(1+0,8*5)=1000 простые проценты.

S=200*(1+0,8/1)⁵=3779 тыс. руб. (за год).

S=200*(1+0,8/2)¹⁰=5785 тыс. руб. (за полгода).

S=200*(1+0,8/4)²⁰=7667 тыс. руб. (квартальная ставка).

Эффективная сумма – годовая ставка, которая дает доход, равный начисляемому по периодам.

Задача: Определить современную текущую величину суммы 100 млн. руб., выплачиваемую через 3 года при использовании ставки сложных процентов(%), при ставке 200% годовых.

Решение: S=P*(1+y/m)^N отсюда 100=P*(1+2)³ или P=100000000/27=3703703,704

Ответ:P=3703703,704

Дисконтирование по сложной процентной ставке.

P=S/(1+i)ⁿ – коэффициент дисконтирования по сложным ставкам процента(%).

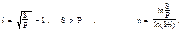
Задача: Найти срок удвоения капитала при годовой ставке i=240% (сложные проценты)

Решение: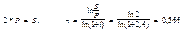

Ответ: n=0,566

Задача: Какова должна быть ставка ссудного процента, чтобы первоначальная сумма утроилась за 2 года.

Решение: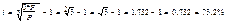

Если начисление по полугодиям:

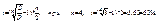
Задача: Первоначальная сумма долга – 30000 рублей. Определить наращенную сумму через 2,5 года, если ставка 200% годовых. Решить 2-мя способами. Сложные процентные ставки.

Решение: 1-ый способ: S=P*(1+i)ⁿ=30*(1+2)^2,5=467,65

2-ой способ: (1+i)^N*(1+i/2)*30=(1+2)²*(1+1)*30=540 (С учетом периодов).

Где i – годовая ставка, i/2 – по полугодиям, N- количество лет.

Коэффициент дисконтирования (приведения):