Показатели асимметрии и эксцесса. Симметричные ряды встречаются крайне редко
Симметричные ряды встречаются крайне редко 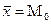 . Для характеристики асимметрии используют несколько показателей:
. Для характеристики асимметрии используют несколько показателей:
1. Самый простой: Аs= 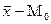 Аs>0 вытянут вправо (правосторонняя асимметрия)
Аs>0 вытянут вправо (правосторонняя асимметрия)
Аs<0 вытянут влево (левосторонняя асимметрия)
2. Для сравнения асимметрии в нескольких рядах используется показатель относительный
Аs =( 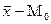 )/σ
)/σ
3. Наиболее часто используют центральный момент третьего порядка
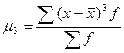
μ>0 правосторонняя асимметрия
μ<0 левосторонняя асимметрия
Показатель эксцесса характеризует крутость распределения. При одной и той же средней арифметической ряд может быть островершинным и низковершинным.
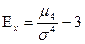
Если 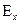 >0 – островершинный
>0 – островершинный
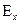 <0 – низковершинный
<0 – низковершинный
Пример. Расчет асимметрии.
| Группы фирм по стоимости основных фондов, млн.р. | Количество фирм | Середина интервала |
| 0,5-1,0 | 0,75 | |
| 1,0-1,5 | 1,25 | |
| 1,5-2,0 | 1,75 | |
| 2,0-2,5 | 2,25 |
Итого 105
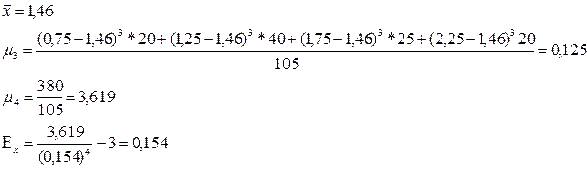
Показатель асимметрии
Основан на соотношении показателей центра распределения: чем больше разница между 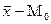 или
или 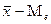 , тем больше асимметрия ряда. При этом, если (
, тем больше асимметрия ряда. При этом, если ( 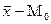 )>0, асимметрия правосторонняя.
)>0, асимметрия правосторонняя.
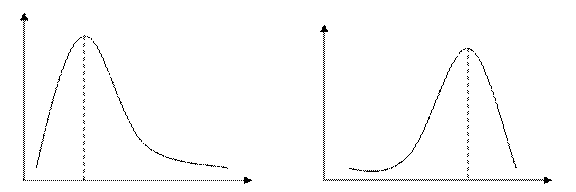
правосторонняя левосторонняя
М0<Ме< 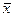 Мо>Ме>
Мо>Ме> 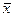
Если ( 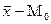 )<0 – асимметрия левосторонняя.
)<0 – асимметрия левосторонняя.
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель:

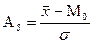 или
или 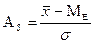
Величина АS может быть положительна и отрицательна. Положительная величина указывает на наличие правосторонней асимметрии, при этом существует следующее соотношение между показателями: М0<Ме< 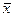
Отрицательный знак показателя асимметрии свидетельствует о левосторонней асимметрии: М0>Ме> 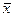 .
.
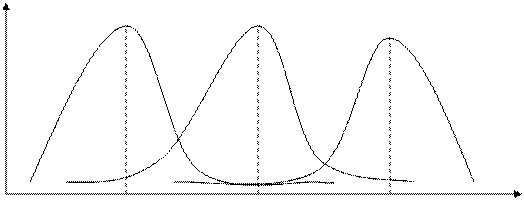
2 1 3
1- нормальное распределение
2 – левосторонняя асимметрия
3 – правосторонняя асимметрия
Другой показатель, предложенный Линдбергом, рассчитывают по формуле
AS=n – 50
где n - % тех значений признака, которые превосходят по величине средн. арифметич.
Наиболее общим является распределение, известное как нормальное, которое может быть представлено графически в виде симметричной колокообразной кривой. Но это бывает крайне редко.
Куполообразная форма кривой показывает, что большинство значений концентрируются вокруг центра измерения.
Закон нормального распределенияпредполагает, что отклонение от среднего значения является результатом большого количества мелких отклонений, что позитивные и негативные отклонения равновероятны и что наиболее вероятным значением всех в равной мере надежных измерений является их арифметическая средняя.
Кривая распределения, выражающая общую закономерность данного типа распределения, называется теоретической кривой распределения.
Фактическое распределение отличается от теоретического в силу влияния случайных факторов. Их влияние сглаживается с увеличением V исследуемой совокупности. Большое значение имеет сопоставление фактических кривых распределения с теоретическими.
Уравнение нормальной кривой выражено посредством 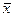 и стандартного отклонения L.
и стандартного отклонения L.
В действительностикривая может иметь вытянутую форму (там, где вокруг средней арифметической концентрируется огромное большинство зарегистрированных значений) и приплюснутую форму (когда отклонения от средней относительно велики).
Необходимо запомнить
В этих пределах заключено
около 68% общей площади
кривой
L L
1. 
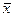
2. 68% общего числа частот
2L 2L

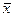
99,73% общего числа частот
3L 3L
3. 
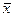
99,994% всей площади
4L 4L
4. 
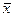
Пример. 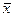 нормального распределения = 1200, L = 2, то известно, что не менее 68% всех наблюдений лежат между значениями 98 и 102 и что почти все наблюдения 99,73% от 94 до 106.
нормального распределения = 1200, L = 2, то известно, что не менее 68% всех наблюдений лежат между значениями 98 и 102 и что почти все наблюдения 99,73% от 94 до 106.
Показатель эксцесса
Для симметричного распределения рассчитывается показатель эксцесса (островершинности).
Эксцесс – выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Линдберг предложил следующий показатель
Ех = n – 38,9, где n – доля (%) количества вариантов, лежащих в интервале, = ½Б в ту или другую сторону от 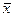 .
.
Наиболее точным является показатель, использующий центральный момент четвертого порядка
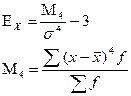
В кривой нормального распределения
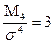
Если ЕХ>0, то эксцесс считают положительным (распределение островершинное).
Если ЕХ<0, то эксцесс отрицательный (распределение низковершинное).
Пример.
Итоги сдачи экзамена по математике студентов 1 курса.
| Получаемые оценки и баллы | Кол-во студентов, получивших данную оценку | |||||
| х | f | xf | |x- 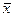 | | | |x- 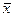 |f |f | (x- 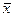 )2 )2 | (x- 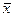 )2f )2f |
| 1,6 | 6,4 | 2,56 | 10,24 | |||
| 0,6 | 4,8 | 0,36 | 2,88 | |||
| 0,4 | 2,8 | 0,16 | 1,12 | |||
| 1,4 | 8,4 | 1,96 | 11,76 | |||
| Итого: | 4,0 | 22,4 | 5,04 | 26,00 |
1. 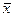 =90/25=3,6
=90/25=3,6
2. L=22,4/25=0,9
3. σ2=26/25=1,04
4. σ= 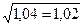
5. Показатель асимметрии А3= 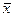 -М0=3,6-3=0,6, следовательно, график будет вытянут вправо.
-М0=3,6-3=0,6, следовательно, график будет вытянут вправо.
6. Показатель эксцесса
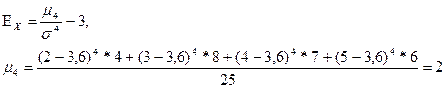
σ4=1,042=1,08
Ех=2/1,08-3=-1,15 Распределение низковершинное.
