Глава 4. наращение процентов и инфляция

В четвертой главе рассмотрены вопросы, связанные с обесценением денег при инфляции. Основная цель данной главы заключается в том, чтобы обосновать использование математики сложных процентов для описания инфляции. Проблема инфляции в данной главе рассматривается с двух точек зрения: обесценение денег при инфляции и защита от инфляции.

Инфляция является объективным фактором, присущим развитию экономики не только нашей страны, но и зарубежных стран. В странах с развитой экономикой – США, Японии, ФРГ, Великобритании, Франции и других – инфляционные процессы происходят непрерывно, хотя их интенсивность относительно низкая.

Инфляция характеризуется обесценением национальной валюты (т.е. снижением ее покупательной способности) и общим повышением цен в стране. В различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценения денежных средств, то заемщик может получить возможность погасить задолженность деньгами сниженной покупательной способности.

Инфляцию необходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции.

Обозначим I_p – индекс цен(индекс инфляции) за период времени от t₀ до T

I_p = ,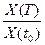

где X(T), X (t₀) – цены в соответствующие периоды времени.

Обозначим H – темп инфляции за период от t₀ до T (в %)

H = (%).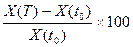

Индекс цен и темп инфляции связаны соотношением:

H = (I_p - 1)×100

I_p = 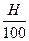+ 1.

Индекс цен I_p показывает во сколько раз выросли цены за период, а темп инфляции – на сколько процентов выросли цены. Например, за два года цены выросли на 130%. Индекс цен I_p = 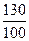+ 1 = 2,3, т.е. цены за два года выросли в 2,3 раза.

Темп инфляции по своей математической природе аналогичен ставке процентов i, а рост цен аналогичен начислению сложных процентов, так как приращение цены идет к цене в предшествующем периоде. Поэтому для описания инфляции можно использовать математику сложных процентов.

Обозначим h_t – темп инфляции за срок t. Тогда за весь период 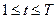множитель наращения будет равен .

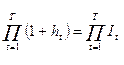Индекс инфляции I_p за весь период равен произведению индексов цен за соответствующие периоды. Например, помесячный рост цен составил 25%, 20%, 18%, тогда индекс инфляции за три месяца определяется как

I_p = 1,25 × 1,2 × 1,18 = 1,77 ,

т.е., за три месяца цены выросли в 1,77 раза или на 77%. Предположим, что темп инфляции – постоянная величина. Обозначим через h – годовой (месячный) темп инфляции, тогда за срок T индекс цен равен

I_p = .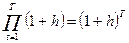

Например, месячный темп инфляции составляет 10%, тогда за год

I_p = (1 + 0,1)¹² = 3,138 Н = (3,138 - 1) ×100 = 213,8%,

т.е., за год цены выросли в 3,138 раза или на 213,8%.

Вернемся к проблеме обесценения денег при их наращении. В общем случае можно записать:

С = ,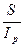

где S – наращенная сумма денег, измеренная по номиналу;

С – эта же сумма денег с учетом ее обесценения.

Рассмотрим случай, когда наращение идет попростым процентам.

С = .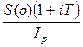

Пример 17.

На сумму 1500 руб. в течение трех месяцев начисляются простые проценты по ставке 18% годовых (К = 360). Определить реальные результаты, если месячная инфляция составляет 10%.

Решение:

С = 1500 × 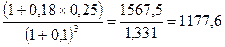(руб.)

Как видно происходит обесценение капитала.

Если наращение идет по сложной ставке процентов, то сумма денег с учетом их обесценения составит:

С = 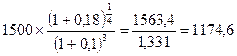(руб.)

Определим процентную ставку, которая компенсирует инфляцию. Для простых процентов приравняем множитель наращения к 1.

.

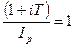Обозначим искомую процентную ставку i*

i* = .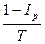

Для сложных процентов i* = h. Ставку, превышающую i* называют положительной ставкойпроцента.

Например, в примере 17 для простых процентов

i* = 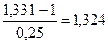или 132,4%,

т.е., процентная ставка выше i* = 132,4% годовых обеспечит реальный доход финансовой операции. Для сложных процентов годовая процентная ставка i*=(1 + 0,1)¹²–1 = 213,8%.

В целях защиты от обесценения денег используются различные методы. Наиболее распространенным является корректировка ставки процентов, по которой осуществляется наращение, т.е. увеличение ставки на величину так называемой инфляционной премии, иначе говоря, производится индексация ставки. Итоговую процентную ставку называют брутто-ставкой.

Брутто-ставка включает инфляционную премию и обеспечивает заданную доходность финансовой операции при известном темпе инфляции. Брутто-ставка отличается от положительной ставки процентов, так как положительная ставка является пограничной: процентные ставки, превышающие ее, обеспечивают доход от финансовой операции. Брутто-ставка не просто обеспечивает доход при известном темпе инфляции, а обеспечивает заданную доходность.

Рассмотрим методы определения брутто-ставки. В случае простых процентов брутто-ставку (обозначим ее r) определим из равенства

1 + rT = (1 + iT)I_p

r = .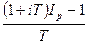

В случае сложных годовых процентов брутто-ставку определяем из равенства:

1 + r = (1 + i) (1 + h)

r = i + h + i×h .

Например, в примере 17 для простых процентов

r = ,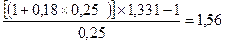

т.е. процентная ставка 156% годовых обеспечивает заданную доходность операции 18% годовых при месячном темпе инфляции 10%.

Для случая сложных процентов

r = 0,18 + 2,138 + 0,18 × 2,138 = 2,7 (270%).

Используя ставку 270% годовых можно обеспечить доходность финансовой операции 18% годовых при темпе инфляции 10% в месяц.

Если наращение идет по номинальной ставке сложных процентов с числом начисления процентов в году m раз, то брутто-ставка r_H определяется из равенства

.

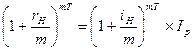
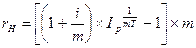Пример 18.

Первоначальный капитал в размере 20000000 руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.

Решение:

Индекс цен I_p за три года равен (1 + 0,12)³ = 1,4

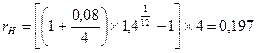
S (З) = 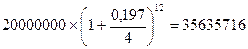(руб.)

Рассмотрим обратную задачу – измерение реальной ставки процента – т.е. определение i по заданному значению брутто-ставки. Если r – объявленная норма доходности (брутто-ставка), то исходный показатель доходности в виде годовой процентной ставки i можно определить при начислении простых процентов как

.

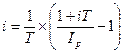Аналогичный показатель находится при наращении по сложным процентам:

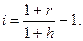
Пример 19.

Определить, какой реальной убыточностью обладает финансовая операция, если при уровне инфляции 14 % в год капитал К вкладывается на один год под номинальную ставку 8 % при ежемесячном начислении.

Решение:

С = К 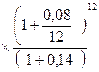= 0,949 К

Таким образом, реальная убыточность финансовой операции составила 5 %. (Первоначальный капитал К уменьшился на 5 %).

В работе Башарина Г.П., представленной в Хрестоматии ЭУМК изложены вопросы учета инфляции в принятии финансовых решений.

Контрольные вопросы

1. Дайте определение индекса инфляции, темпа инфляции. В чем различие между ними?

2. Назовите методы защиты от инфляции.

3. Почему для описания инфляции используется математика сложных процентов?

4. Как определяется брутто-ставка в случае простых процентов (сложных процентов)?