Типовые примеры и методы их решения 3 страница

2.1.51. Клиент поместил в банк некоторую сумму под слож­ную процентную ставку 30% годовых. В конце каждого года клиент расходует четвертую часть наращенной к этому моменту суммы. Через сколько лет наращенная сумма доставит 85% от первоначальной величины помещенных денежных средств?

2.1.52. Господин N поместил в банк на 6 лет свободные де­нежные средства под сложную процентную ставку 40% годо­вых. Какую часть наращенной суммы в конце каждого года (включая последний) господин N должен расходовать, чтобы в конце шестого года наращенная сумма составила по величине половину помещенных вначале денежных средств?

2.1.53. На сумму 15 тыс. руб. в течение четырех лет ежегод­но начисляются простые проценты по процентной ставке 40% годовых, а на все начисленные проценты ежегодно осуществля­ется наращение сложных процентов по процентной ставке 30% годовых. Определите величину наращенной суммы в конце чет­вертого года.

2.1.54. Определяется приведенная стоимость некоторой де­нежной суммы при двух сложных годовых процентных ставках: 30 и 40%. Найдите срок, за который необходимо осуществить дисконтирование, чтобы разность между полученными приве­денными стоимостями была наибольшей.

2.1.55. Предприниматель получил в банке кредит на 6 лет по процентной ставке 28% годовых, при этом банком были удер­жаны комиссионные в размере 2% от величины кредита. Найди­те доходность такой финансовой операции для банка в виде эф­фективной процентной ставки, если банк начисляет ежеквар­тально сложные проценты на исходную сумму кредита. Изме­нится ли доходность при выдаче кредита на 3 года?

2.1.56. В банке получен кредит на 5 лет по процентной став­ке 24% годовых, при этом банком были удержаны комиссион­ные в размере 1% от величины кредита. Найдите доходность такой финансовой операции для банка в виде эффективной про­центной ставки, если банк начисляет сложные проценты на ис­ходную сумму кредита: а) ежегодно; б) ежеквартально; в) еже­месячно.

2.1.57. Выдана ссуда под процентную ставку 32% годовых, при этом сразу были взысканы комиссионные в размере 2,5% от величины ссуды. Определите доходность такой сделки в виде годовой эффективной процентной ставки, если кредитор начисляет простые проценты на исходную величину ссуды и срок ссуды: а) 4 года; б) 8 лет. Как изменится доходность, если ко­миссионные не будут удерживаться?

2.1.58. Банк выдает ссуду на 3 года под годовую номиналь­ную процентную ставку 24%, причем сложные проценты начис­ляются ежеквартально на исходную сумму ссуды. Определите доходность такой финансовой операции для банка в виде эф­фективной процентной ставки, если: а) комиссионные не удер­живаются; б) удерживаются комиссионные в размере 2% от ве­личины ссуды; в) удерживаются комиссионные в размере 2% от величины ссуды и ее срок увеличивается до 5 лет.

2.1.59. Выдается ссуда по процентной ставке 35% годовых, при этом взимаются комиссионные в размере 1,5% от величины ссуды. Сложные проценты начисляются ежемесячно на исход­ную величину ссуды. На какой срок должна быть выдана ссуда, чтобы доходность такой сделки для кредитора в виде годовой эффективной процентной ставки составляла 45%?

2.1.60. При выдаче кредита на 7 лет по процентной ставке 30% годовых были удержаны комиссионные. Сложные процен­ты начислялись ежегодно на исходную величину кредита. Сколько процентов составили комиссионные от величины кре­дита, если доходность такой финансовой операции для банка в виде эффективной процентной ставки получилась равной 31,2% годовых?

2.1.61. Вексель учитывается банком за 3 месяца до его пога­шения по простой учетной ставке 24% годовых. Определите до­ходность такой финансовой операции для банка в виде эффек­тивной процентной ставки, если: а) комиссионные не удержи­ваются; б) удерживаются комиссионные в размере 2,5% от сум­мы, выплачиваемой за вексель; в) удерживаются комиссионные в размере 2,5% от суммы, выплачиваемой за вексель, и вексель учитывается за б месяцев до его погашения.

2.1.62. Предлагается оформить вклад под следующие про­центные ставки: 200% годовых или 35% за квартал, причем в обоих случаях используется смешанная схема начисления про­центов. Какой вариант выгоднее, если срок хранения вклада со­ставляет: а) 6 месяцев; б) один год? До какого срока выгоднее иметь 200% годовых, а когда выгоднее ежеквартальное начис­ление по 35%? Финансовый год принять равным 360 дней (ме­сяц-30 дней).

2.1.63. Инвестор собирается разместить эффективно свои свободные денежные средства. Если он вложит средства в цен­ные бумаги трастовой компании, то должен будет заплатить на­лог с получснвой прибыли в размере 8%. Если же он положит деньги в банк, то начисленные проценты не будут облагаться налогом. Определите, наиболее прибыльную схему вложения капитала с 1 января по 31 марта, если налоги платятся в конце каждого квартала и услуги на финансовом рынке предлагают две фирмы: трастовая компания - на условиях начисления сложных процентов по процентной ставке 5% за месяц по вкла­ду, составляющему целое число месяцев, но не менее месяца; банк - с ежемесячным начислением сложных процентов по го­довой номинальной процентной ставке 48% годовых при таких же ограничениях на срок вклада.

2.1.64. Вкладчик может свои свободные денежные средства в долларах на один год поместить в одном банке на валютном де­позите под процентную ставку 13% годовых с полугодовым на­числением сложных процентов или в другом банке эту же сумму поместить на рублевом депозите под процентную ставку 16% годовых с ежеквартальным начислением сложных процентов. Как ему лучше поступить, если курс покупки долларов на нача­ло срока - 19 руб. 80 коп., а ожидаемый курс продажи через год - 21 руб. 50 коп.?

2.1.65. Господин N намеревается обменять имеющиеся у не­го немецкие марки и поместить полученную сумму на рублевом депозите сроком на 3 года под процентную ставку 24% годовых с ежеквартальным начислением сложных процентов, после чего наращенную сумму опять конвертировать в немецкие марки. При каком ожидаемом курсе продажи не имеет смысла такая финансовая операция, если курс покупки немецких марок на начало срока составляет 10 руб. 64 коп. и на валютном депозите денежную сумму можно поместить под процентную ставку 18% годовых с ежемесячным начислением сложных процентов?

2.1.66. Некоторая сумма в долларах США обменивается на рубли, после чего помещается на рублевый депозит на 2 года 6 месяцев под процентную ставку 30% годовых с ежегодным начислением сложных процентов. Полученная наращенная сум­ма опять конвертируется в доллары США. Определите доход­ность такой финансовой операции в виде годовой эффективнойпроцентной ставки, если курс покупки долларов на начало сро­ка- 18 руб. 20 коп., а курс продажи через 2 года б месяцев -22 руб. 14 коп. и начисление процентов осуществлялось: а) по схеме сложных процентов; б) по смешанной схеме.

2.1.67. На вклад 100 тыс. руб. по истечении 4 лет были на­числены сложные проценты по годовой номинальной процент­ной ставке 32% исходя из полугодовой схемы начисления. Оп­ределите наращенную сумму после уплаты налога на проценты, если налог на все полученные проценты выплачивается один раз в конце срока и ставка налога на проценты равна 15%.

2.1.68. На вклад 150 тыс. руб. в течение 6 лет раз в год на­числялись сложные проценты по годовой номинальной про­центной ставке 26% исходя из полугодовой схемы начисления. Определите итоговую наращенную сумму после уплаты налога на проценты, если налог на проценты уплачивается каждый год путем выделения средств из накапливаемой суммы и ставка на­лога на проценты равна 12%. Чему равна величина налога за ка­ждый год?

2.1.69. На депозит была помещена сумма 80 тыс. руб. на 2 года 6 месяцев, по истечении которых были начислены слож­ные проценты по годовой процентной ставке 30%. Определите наращенную сумму после уплаты налога на проценты, если ставка налога на проценты равна 12%, налог на все полученные проценты выплачивается один раз в конце срока и наращение осуществлялось: а) по схеме сложных процентов; б) по смешан-ной схеме.

2.1.70. Инвестор собирается вложить 40 тыс. руб. с целью получения после уплаты налога на проценты 100 тыс. руб. на следующих условиях: по истечении оговоренного в контракте срока на инвестируемую сумму будут начислены сложные про­центы по годовой номинальной процентной ставке 30% исходя из ежемесячной схемы начисления. Определите срок, необходи­мый для накопления требуемой суммы, если ставка налога на проценты равна 15% и налог на все полученные проценты вы­плачивается один раз в конце срока. Какой будет срок, если на­лог на проценты не надо уплачивать?

2.1.71. Инвестор собирается вложить 20 тыс. руб. с целью получения после уплаты налога на проценты 70 тыс. руб. на следующих условиях: в течение оговоренного в контракте срока разв год на инвестируемую сумму будут начисляться сложные проценты по годовой номинальной процентной ставке 32% ис­ходя из ежемесячной схемы начисления. Определите срок, не­обходимый для накопления требуемой суммы, если ставка нало­га на проценты равна 15% и налог на проценты уплачивается каждый год путем выделения средств из накапливаемой суммы. Какой будет срок, если налог на проценты не надо уплачивать?

2.1.72. На вклад по истечении 5 лет были начислены слож­ные проценты по годовой номинальной процентной ставке 34% исходя из ежеквартальной схемы начисления, причем один раз в конце срока был выплачен налог на все полученные про­центы. Определите годовую эффективную процентную ставку в этой финансовой сделке, если ставка налога на проценты равна 15%.

2.1.73. Предприниматель инвестировал 120 тыс. руб. на блет, по истечении которых были начислены сложные проценты по переменной годовой процентной ставке, причем для первых трех лет годовая процентная ставка равнялась 22%, на следующие два года устанавливалось 28% и на последний год - 30%. Определите наращенную сумму после уплаты налога на проценты, если став­ка налога на проценты равна 15% и налог на все полученные про­центы выплачивается один раз в конце срока.

2.1.74. Предприниматель инвестировал 200 тыс. руб. на 4 го­да, в течение которых раз в год начислялись сложные проценты по переменной годовой процентной ставке, причем для первых двух лет годовая процентная ставка равнялась 30%, на следую­щий год устанавливалось 34% и на последний год - 36%. Опре­делите итоговую наращенную сумму после уплаты налога на все проценты, если ставка налога на проценты равна 15% и налог на проценты уплачивается каждый год путем выделения средств из накапливаемой суммы.

2.1.75. Вклад 160 тыс. руб. был размещен в банке на 2 года и 8 месяцев, по истечении которых на этот вклад были начислены сложные проценты по годовой номинальной процентной ставке 30% и вклад был востребован. После уплаты налога на процен­ты вкладчик стал обладателем суммы в размере 299,808 тыс. руб. Какую схему начисления процентов использовал банк, если ставка налога на проценты равна 15% и налог на все полученные проценты выплачивается один раз в конце срока?

Сложная учетная ставка

Основные положения

• Дисконтирование по сложной учетной ставке осуществля­ется в ситуации предварительного начисления сложного про­цента, т.е. когда сложный процент (например, за кредит или за продажу некоторого финансового документа до срока его пога­шения) начисляется в момент заключения финансового согла­шения. В этом случае в начале каждого периода начисления проценты начисляются не на одну и ту же величину (как при дисконтировании по простой учетной ставке), а каждый раз на новую, полученную в результате дисконтирования, осуществ­ленного в предыдущем периоде.

• Для лица, осуществляющего предварительное (антисипа-тивное) начисление процентов, а следовательно, и дисконтиро­вание, более выгодным является дисконтирование по сложной учетной ставке, если срок учета менее одного года; более вы­годным является дисконтирование по простой учетной ставке, если срок учета превышает один год; дисконтирование в обоих случаях дает один и тот же результат, если срок учета равен од­ному году.

• Если срок, за который осуществляется дисконтирование, не равен целому числу лет, то при определении стоимости учтен­ного капитала, как правило, используют либо сложную учетную ставку, либо смешанную схему (применяется сложная учетная ставка для целого числа лет и простая учетная ставка - для дробной части года). Стоимость учтенного капитала будет больше при использовании смешанной схемы. Аналогичные способы дисконтирования применяются и в том случае, когда дисконтирование производится не один, а несколько раз в году.

• С ростом в году числа операций дисконтирования по номи­нальной учетной ставке величина учтенного капитала возра­стает.

• Эффективная годовая учетная ставка обеспечивает тот же результат, что и дисконтирование несколько раз в году по номи­нальной учетной ставке, деленной на число периодов дисконти­рования.

• Эффективная учетная ставка определяется и как ставка, обеспечивающая переход от исходной суммы к учтенной при однократном дисконтировании за базовый период (например, за год), т.е. не используется явным образом номинальная учетная ставка.

Вопросы для обсуждения

1.В каких случаях может осуществляться дисконтирование по сложной учетной ставке?

2.Опишите подробно, как осуществляется дисконтирование по сложной годовой учетной ставке при продаже некоторого долгового обязательства за три года до срока погашения. 3.Какой вид имеет множитель дисконтирования при дисконти­ровании по сложной учетной ставке?

4.Как связаны между собой дисконтирование по сложной учетной ставке и проценты "со 100"?

5. Как соотносятся величины дисконтированных сумм при дис­контировании по простой и по сложной учетным ставкам?

6. Как соотносятся величины дисконтированных сумм при дис­контировании по сложной учетной и по сложной процентной ставкам?

7. Как соотносятся величины дисконтированных сумм при дис­контировании по простой процентной и по сложной учетной ставкам?

8. Какие два основных способа дисконтирования, связанные со сложной учетной ставкой, вы знаете? Какой из них выгоднее для лица, осуществляющего учет?

9. Может ли учет по сложной учетной ставке привести к недо­пустимым на практике величинам?

10. Какая годовая учетная ставка называется номинальной?

11. Что происходит с величиной учтенного капитала, если рас­тет число осуществлений операции дисконтирования по сложной учетной ставке?

12. Какая ставка называется эффективной годовой учетной ставкой? От каких параметров она зависит?

13. Как ведет себя эффективная годовая учетная ставка с увели­чением числа периодов дисконтирования в году?

14. Как пояснить с финансовой точки зрения соотношение меж­ду эффективной и номинальной учетными ставками?

15. В каком случае эффективная годовая учетная ставка совпа­дает с номинальной?

16. Что происходит с величиной номинальной учетной ставки при определении ее через эффективную годовую учетную ставку, когда число операций дисконтирования в году растет?

17. Какие номинальные учетные ставки называются эквива­лентными?

18. Приведите формулу наращения по сложной учетной ставке.

19. Как можно связать между собой наращение по сложной учетной ставке и проценты "во 100"!

20. Какая из ставок, сложная учетная или такая же по величине сложная процентная, обеспечивает более быстрый рост ка­питала при наращении?

21. Как соотносятся между собой результаты наращения по простой процентной и сложной учетным ставкам?

22. Что можно сказать о декурсивном и антисипативном спосо­бах начисления сложных процентов, когда период начисле-ния уменьшается?

. Типовые примерыи методы их решения

Пример 2.2.1.Найдите величину дисконта, если долговое обязательство на выплату 40 тыс. руб. учтено за 3 года до срока погашения по сложной учетной ставке: а) 20% годовых; б) 25% годовых.

Решение,а) Полагаяп = 3 , F₃= 40 тыс.руб. d = 0,2 по формуле (67) получим:

Р = 40(1 - 0.2)³ = 20,48 тыс. руб.

Поэтому дисконт составит:

D_d =40-20,48 = 19,52 тыс.руб.

б) Так как в этом случае d = 0,25 „ то

Р=40(1-0,25)³ =16,875 тыс. руб.,

D_d =40-16,875 = 23Д25 тыс. руб.

Видно, что с ростом учетной ставки уменьшается дисконти­рованная величина выплаты по долговому обязательству и, сле­довательно, увеличивается величина дисконта.

Пример 2.2.2.Вексель на сумму 70 тыс. руб. со сроком по­гашения через 4 года учтен за 32 месяца по сложной учетной ставке 24% годовых. Определите суммы, которые получит предьявитель векселя при различных способах учета векселя.

Решение. При применении только сложной учетной ставки воспользуемся формулой (67). Так как дисконтирование произ­водится один раз в год, то n = 32/12 = 8/3. Далее F_n =70 тыс. руб., d = 0,24, поэтому:

Р = 70(1-0,24) 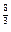=33,672 тыс. руб.

Если же использовать при учете смешанную схему, то при w = 2, f=2/3 по формуле (68) получим:

Р = 70(1 – 0,24)² (1 - 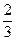0,24) = 33,963 тыс. руб.

Таким образом, предъявитель векселя получит больше при использовании смешанной схемы.

Пример2.2.3. Рассчитайте дисконтированную сумму при учете 1 млн руб. по простой и сложной учетным ставкам, если годовая учетная ставка равна 18% годовых и учет происходит за 30 дней, 90 дней, 180 дней, 1 год, 2 года, 3 года, 5 лет. Полагать каждый год равным 360 дней.

Решение.Применяя при F = F_n =1 млн руб. и d = 0,18 для простой учетной ставки формулу (19), а для сложной - формулу (67), получим следующие результаты, представленные для на­глядности в табличном виде:

(млн руб.)

Способ дисконтиро­вания	30 дней (n=1/12)	90 дней (n=1/4)	180 дней (n=1/2)	1 год (n=1)	2 года (n=2)	3 года (n=3)	5 лет (n=5)
Простая учет­ная ставка	0,985	0,955	0,91	0,82	0,64	0,46	0,1
Сложная учет­ная ставка	0,9836	0,9516	0,9055	0,82	0,6724	0,5514	0,3707

Таким образом, если вексель на сумму 1 млн руб. учитывает­ся, когда до срока погашения остается меньше года, то для вексе­ледержателя более выгоден учет по простой учетной ставке. Так, при учете за 90 дней до срока погашения векселедержатель полу­чит: при использовании простой ставки - 955 тыс. руб.; при ис­пользовании сложной учетной ставки - 951,6 тыс. руб., т.е. раз­ница между суммами составляет 3,4 тыс. руб. Если же учет век­селя осуществляется, когда до срока погашения остается больше года, то для векселедержателя более выгоден учет по сложной учетной ставке.

Заметим, что дисконтирование по простой учетной ставке за срок более чем 5,56 года, приводит к не допустимым на практике величинам (будем получать отрицательные значения дисконтиро­ванных сумм). Однако учет по сложной учетной ставке всегда дает положительные дисконтированные величины. Например,

при учете за 15 лет получим: Р = 1*(1-0,18)¹⁵ =0,0510 млн руб.

Пример 2.2.4. Долговое обязательство на выплату 46 тыс. руб. учтено за 4 года до срока погашения. Определите полученную сумму, если производилось: а) полугодовое; б) поквартальное; в) помесячное дисконтирование по номинальной учетной ставке 24% годовых.

Решение. Во всех случаях полагаем n = 4, F_n = F₂ =46 тыс. руб. и пользуемся формулой (69).

а) Так как т =2, d^(m) =d⁽²⁾ =0,24, то:

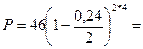16,543 тыс. руб.

б) Поскольку т = 4, d ^(m) = d^{4) = 0,24, то:

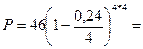=17,092 тыс. руб.

в) В этом случае m = 12, d^(m) =d⁽¹²⁾ =0,24, поэтому:

17,443 тыс.руб.

Сравнивая полученные результаты, видим, что с ростом чис­ла осуществлений операции дисконтирования в году величина учтенного капитала возрастает.

Пример 2.2.5. Определите, какую сумму получит владелец векселя на 30 тыс. руб. со сроком погашения через 25 месяцев, если он учтет вексель сразу при его выдаче по номинальной учетной ставке d 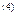= 20% годовых. Сравните два способа дис­контирования.

Решение. Полагаем n=25/12, m = 4, F_n = 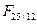тыс. руб. Если использовать формулу (69), то

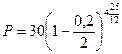= 19,565 тыс.руб.

Пусть дисконтирование осуществляется по смешанной схеме по формуле (70). Поскольку

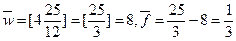
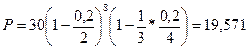тыс.руб.

Очевидно, для векселедержателя выгоднее смешанная схема.

Пример 2.2.6. За долговое обязательство в 80 тыс. руб. бан­ком было выплачено 62 тыс. руб. За какое время до срока пога­шения было учтено это обязательство, если банком использова­лась: а) годовая сложная учетная ставка 28%, б) годовая простая учетная ставка 28%?

Решение, а) Полагая в формуле (71) .Р = 62 тыс. руб.,

F_n = 80 тыс. руб., т = 1, 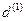= 0,28, получим:

⁶²

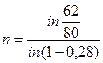= 0,776 года.

Считая, что в году 360 дней, находим n = 360*0,776 = 279,36 дня. Округляя полученный срок до целого числа дней, делаем вывод, что долговое обязательство было учтено за 280 дней до срока погашения. б) В случае простой учетной ставки воспользуемся форму­лой (22), где F = 80 тыс. руб., d = 0,28:

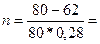0,804 года, или 289,44 дня.

Таким образом, n = 290 дней.

Пример 2.2.7.Вексель был учтен за 2,5 года до срока пога­шения, при этом владелец векселя получил четверть от напи­санной на векселе суммы. По какой годовой номинальной учет­ной ставке был учтен этот вексель, если производилось: а) по­квартальное дисконтирование; б) помесячное дисконтирование?

Решение,а) Применяя формулу (72), в которой P = 0,25F_{n ,}п = 2,5 , т = 4, получим:

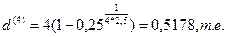
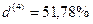
б) Если m=12,то

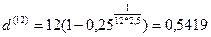т.е. 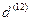=54,19%.

Таким образом, чем большее количество раз в году произво­дится дисконтирование, тем больше величина годовой номи­нальной учетной ставки.

Пример 2.2.8.Рассчитайте эффективную годовую учетную ставку при различной частоте начисления дисконта и номиналь­ной учетной ставке, равной 18% годовых.

Решение. Используя формулу (74), вычислим для некоторых значений т эффективную годовую учетную ставку и результа­ты запишем в табличном виде:

т
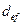	0,18	0,1719	0,1682	0,1659	0,1653	0,1648

Из таблицы следует, что d_ef уменьшается с ростом т (так как

второе слагаемое в правой части равенства (74) увеличивается). Вообще можно показать, что при т > 1 справедливо неравенство

d_ef < d^(m), которое нетрудно пояснить и из финансовых сообра-

жении.

Пример 2.2.9.Определите номинальную учетную ставку, если годовая эффективная учетная ставка равна 30% и дискон­тирование по сложной учетной ставке осуществляется: а) каж­дые полгода; б) ежемесячно; в) ежеквартально.

Решение.Полагаем 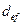= 0,3 и пользуемся формулой (73).

а) Так как т = 2, то

d⁽²⁾ =2[1-(l-0,3) 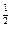] = 0,3267, или 32,67%.

б) Поскольку в этом случае т = 12 , то

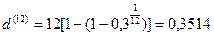, или 35,14%.

в) Считая в году 360 дней, при т = 360 получим:

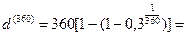0,3565, или 35,65% .

Найденные номинальные ставки d⁽²⁾, d⁽¹²⁾ и d⁽³⁶⁰⁾ эквива­лентны, так как они получены в соответствии с одной и той же эф­фективной ставкой. Поэтому осуществление дисконтирования раз в год по сложной учетной ставке 30% годовых дает такой же ре­зультат, как осуществление дисконтирования 2 раза в год по ставке 32,67% годовых, или 12 раз в год по ставке 35,14% годовых, или каждый день (360 раз в год) по ставке 35,65% годовых. Отметим,

Что d⁽²⁾<d⁽¹²⁾ < d⁽³⁶⁰⁾, т.е. величина номинальной учетной ставки растет, когда количество осуществлений дисконтирования в году увеличивается. Аналогичное неравенство справедливо и в общем

случае, а именно: пусть d^(m) и 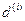эквивалентные номинальные

годовые учетные ставки и m>i, тогда d^(m) >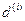

Пример 2.2.10.Вексель на сумму 12 тыс. руб. со сроком по­гашения через 3 года 6 месяцев был сразу же учтен в банке, и предъявитель векселя получил 5 тыс. руб. Найдите эффектив­ную годовую учетную ставку в этой финансовой операции.

Решение.Подставляя в формулу (75) n = 3,5, P = 5 ,F_3,5=12, находим:

d_ef=1- 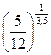= 0,2213,или 22ДЗ%.

Пример 2.2.11.По условиям финансового соглашения на сумму 90 тыс. руб., помещенную в банк на 5 лет, начисляются проценты по сложной учетной ставке 24% годовых. Определите наращенную сумму, если начисление процентов производится: а) по полугодиям; б) ежеквартально; в) ежемесячно. Сравните полученные величины с результатами наращения сложными процентами по процентной ставке 24% годовых.

Решение.Будем пользоваться формулой (77), где Р = 90

тыс. руб., n = 5, d⁽²⁾= d⁽⁴⁾ = d⁽¹²⁾ = 0,24 . Полагая последователь­но т = 2, т = 4, т = 12 , получим:

a) 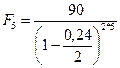= 323,159 тыс. руб.;

b) 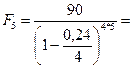310,231 тыс. руб.;

в) 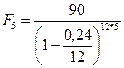=302,467 тыс. руб.

Полезно заметить, что во всех случаях можно было восполь­зоваться и формулой (76), полагая число периодов равным соот­ветственно 10, 20 и 60, а учетные ставки - 12% (24% : 2), 6% (24% : 4) и 2% (24% : 12).

Если бы наращение сложными процентами осуществлялось с помощью процентной ставки, то для вариантов а), б), в) получили бы по формуле (58) следующие значения наращенных сумм:

а) F₅ = 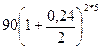=279,522 тыс. руб.;

б) 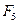= = 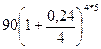288,639 тыс. руб.;

в) 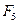= 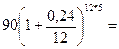295,293 тыс. руб.,

т.е., как уже отмечалось, с увеличением числа начислении про­центов за год по сложной процентной ставке величина нара­щенной суммы возрастает. В противоположность этому с уве­личением числа начислений процентов за год по сложной учет­ной ставке величина наращенной суммы убывает. Видно, что, чем больше число наращений в течение года, тем меньше раз­ница между итоговыми суммами, полученными декурсивным и антисипативным способами начисления процентов. Это и объ­яснимо, поскольку, чем меньше период начисления, тем меньше отличие между понятиями предварительный и последующий. Так, если т = 365 (каждый день идет начисление сложных про­центов), то применение номинальной учетной ставки 24% годо­вых дает 298,928 тыс. руб., а такой же величины процентной ставки - 298,693 тыс. руб., и разница между этими суммами равна уже 235 руб., в то время как, например, при т = 4 соот­ветствующая разница составляет 21 592 руб.