Типовые примеры я методыих решения

Пример 3.3.1.Работник заключает с фирмой пенсионный контракт на 12 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать по 3 тыс. руб. Требуется определить наращенную сумму к концу действия контракта, если на поступающие суммы будут начисляться:

307а) ежегодно сложные проценты по номинальной годовой про­центной ставке 24%; б) ежеквартально сложные проценты по номинальной годовой процентной ставке 24%; в) непрерывные проценты с силой роста 24% за год.

Решение.Денежные поступления образуют постоянный ан­нуитет постнумерандо с A = 3 тыс. руб., сроком n = 12 лети пе­риодом u =2 года. Следовательно, период аннуитета больше базового периода начисления процентов, равного году. Схема­тично это выглядит таким образом:

3 3 3 3 3 3

i i i i i i I i i i i i i

о 1 2 3 4 5 6 7 8 9 10 11 12 t лет

а) В этом случае r =24%, m= 1и по формуле (146) получим:

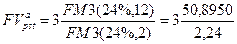= 68163 тыс.руб.

б) Поскольку в этом случае начисление процентов ежеквар­тальное, то т = 4 и по формуле (146) получим:

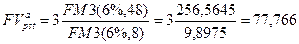тыс. руб.;

в) Полагая 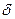= 0,24, по формуле (149) находим:

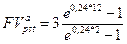= 81,878 тыс. руб.

Пример 3.3.2.Определите сумму, которую необходимо по­местить на счет в банке, чтобы в течение 15 лет в конце каждого трехлетнего периода иметь возможность снимать со счета 8 тыс. руб., причем к концу срока полностью выбрать все деньги со сче­та, если на находящиеся на счете денежные суммы будут начис­ляться: а) ежегодно сложные проценты по ставке 20%; б) каждые полгода сложные проценты по ставке 20%; в) непрерывные про­центы с силой роста 20%.

Решение.Во всех случаях надо определить приведенную стоимость постоянного аннуитета с А = 8 тыс. руб., периодом u = 3 года и сроком n = 15 лет.

а) Так как r =20%, то, применяя формулу (147) при m = 1, получим:

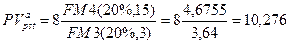тыс. руб.;

б) В этом случае m = 2, r = 20%, и поэтому из формулы (147)-следует, что:

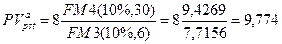тыс. руб.;

в) Поскольку в этом случае начисляются непрерывные про­центы с силой роста 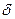= 0,2, то по формуле (150) получим:

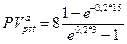= 9,246 тыс. руб.

Пример 3.3.3.На счет в банке в начале каждого двухлетнего периода будет поступать по 8 тыс. руб. в течение 10 лет. Требу­ется определить: а) будущую стоимость аннуитета; б) приведен­ную стоимость аннуитета, если на поступающие суммы будут ежегодно начисляться декурсивные сложные проценты по став­ке 22% годовых.

Решение.Согласно условию имеем аннуитет пренумерандо с членом А = 14 тыс. руб., периодом u = 2 года и сроком n = 10 лет. Сложная процентная ставка r = 22% годовых и число на­числений процентов m =1.

а) В соответствии с формулами (146) и (152) получим:

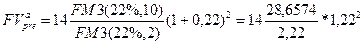= 268,987 тыс. руб.

б) По формулам (147) и (153):

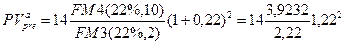=36,824 тыс. руб.

Пример 3.3.4.Предприниматель приобрел оборудование в кредит за 900 тыс. руб. под 25% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать долгнужно равными суммами в конце каждого второго года и вы­платить весь долг за 10 лет. Требуется определить величину ка­ждого платежа и составить план погашения долга.

Решение.Обозначим через А величину каждого искрмого платежа. Поток этих платежей представляет собой аннуитет по-стнумерандо, для которого PV 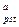=900000 руб., r = 25%,

n = 10, m = 1, u = 2. Поэтому для нахождения величины А можно вос­пользоваться формулой (147), из которой следует:

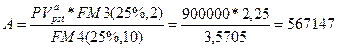тыс. руб.;

Теперь поясним составление плана погашения долга. Посколь­ку в течение первых двух лет предприниматель пользовался креди­том в размере 900000 руб., то платеж, который равен 567147 руб. и будет сделан в конце второго года, состоит из следующих двух частей: сложных процентов за два года в сумме 506250 руб. (900000-[(1+0,25)²-1] руб.) и погашаемой части долга в сумме 567147 - 506250 =60897 руб. В следующем двухлетии расчет бу­дет повторен при условии, что размер кредита, которым пользуется предприниматель, составит уже меньшую сумму по сравнению с первыми двумя годами, а именно: 900000 - 60897 = 839103 руб. Таким образом, сложные проценты за два года будут равны 471995 руб. (839103 -[(1 + 0,25)²-1]руб.), а погашаемая часть долга будет равна 567147 - 471995 = 95152 руб. и т.д. Ясно, что с течени­ем времени сумма уплачиваемых процентов снижается, а доля пла­тежа в счет погашения долга возрастает.

План погашения долга представим в виде таблицы.

(руб.)

Но­мер двух­летия	Остаток ссуды на начало двухлетия	Величина платежа	В том числе	Остаток ссуды на конец двухлетия
			проценты за два года	погашенная часть долга

Поскольку данные в ходе вычислений округлялись, величи­на процентов в последней строке найдена балансовым методом, т.е. вначале записываем погашенную часть долга 362972 руб., азатем определяем величину процентов за два года: 567147 - 362972 = 204175 руб. Если же непосредственно найти сложные проценты за два года от суммы в 362972 руб. исходя из про­центной ставки 25%, то получим 204172 руб. Суммируя величи­ны в пятом столбце, получим размер кредита: 900000 руб.

Задачи

3.3.1. Работник заключает с фирмой пенсионный контракт на 20 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать по 1,5 тыс. руб. Требуется определить наращенную сумму к концу действия контракта, если на поступающие суммы будут ежегодно начис­ляться декурсивные сложные проценты по ставке 18% годовых.

3.3.2. Фирма решила образовать фонд для обеспечения бу­дущих расходов. С этой целью в конце каждых трех лет фирма перечисляет в банк по 25 тыс. руб. Какая сумма будет на счете фирмы через 21 год, если на поступающие суммы будут начис­ляться: а) по полугодиям сложные проценты по номинальной годовой процентной ставке 20%; б) непрерывные проценты с силой роста 20% за год?

3.3.3. Определите сумму, которую необходимо поместить на счет в банке, чтобы в течение 16 лет в конце каждого двухлетне­го периода иметь возможность снимать со счета 5 тыс. руб., причем к концу срока полностью выбрать все деньги со счета, если на находящиеся на счете денежные суммы будут начис­ляться: а) ежегодно сложные проценты по ставке 24%; б) каж­дый квартал сложные проценты по ставке 24%; в) непрерывные проценты с силой роста 24%.

3.3.4. На счет в банке в начале каждого трехлетнего периода будет поступать по 10 тыс. руб. Требуется определить наращен­ную сумму через 15 лет, если на поступающие суммы будут ежегодно начисляться декурсивные сложные проценты по став­ке 23% годовых. 3.3.5. В течение 24 лет каждые четыре года в банк вносится по 40 тыс. руб. по схеме: а) постнумерандо; б) пренумерандо. Банк начисляет сложные проценты каждые полгода из расчета 16% годовых. Какая сумма будет на счете в конце срока?

3.3.6. Страховая компания, заключив на 8 лет договор с неко­торой фирмой, получает от нее страховые взносы по 35 тыс. руб. в конце каждого двухлетнего периода. !>ги взносы компания по­мещает в банк под годовую номинальную процентную ставку 20% годовых. Найдите приведенную стоимость суммы, которую получит страховая компания по данному контракту, если слож­ные проценты начисляются: а) ежегодно; б) ежеквартально; в) непрерывно.

3.3.7. Предприятие в целях создания фонда хочет накопить на своем счете 300 тыс. руб., осуществляя в конце каждого третьего года равные вклады в банк под сложную процентную ставку 25% годовых. Какой величины должен быть каждый вклад, чтобы предприятие могло накопить требуемую сумму за: а) 9 лет; б) 18 лет?

3.3.8. Некоторая фирма хочет создать фонд в размере 350 тыс. руб. С этой целью в конце каждого двухлетнего периода фирма предполагает вносить по 20 тыс. руб. в банк под 28% годовых. Найдите срок, необходимый для создания фонда, если банк на­числяет сложные проценты: а) ежегодно; б) ежеквартально; в) непрерывно.

3.3.9. Какую сумму необходимо поместить в банк под номи­нальную процентную ставку 30% годовых, чтобы в течение 20 лет иметь возможность в конце каждого двухлетнего периода снимать со счета по 10 тыс. руб., исчерпав счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) по по­лугодиям; в) непрерывно?

3.3.10. Имеется переменный аннуитет постяумерандо (тыс. руб.): 4, 2, 1, 8, 5. Рассчитайте: а) будущую стоимость аннуите­та; б) приведенную стоимость аннуитета, если его период равен трем годам и начисление процентов осуществляется по сложной процентной ставке 25% годовых. Как изменятся полученные оценки, если исходный поток представляет собой аннуитет пре-нумераядо?

3.3.11. Получена ссуда на 15 лет в сумме 1 200 тыс. руб. под 20% годовых, начисляемых по схеме сложных процентов на не-

погашенный остаток. Возвращать нужно равными суммами в конце каждого трехлетнего периода. Требуется определить ве­личину каждого платежа и составить план погашения долга.

3.3.12. Перед выходом на пенсию господин N хочет обеспе­чить себе дополнительно по прошествии каждых двух лет доход в сумме 8 тыс. руб. неограниченно долго. Какую сумму он дол­жен поместить в банк, начисляющий сложные проценты по

ставке 24% годовых?

3.3.13. Определит^ текущую (приведенную) стоимость бес­срочного аннуитета постнумерандо с поступлением 4,2 тыс. руб. через каждые четыре года, если предлагаемый государственным банком процент по срочным вкладам равен 28% годовых, при­чем сложные проценты начисляются ежеквартально.

З.ЗЛ4. Кредитор з")цслючил контракт, согласно которому должник обязуется выплатить 100 тыс. руб. за 8 лет равными суммами в конце каждого двухлетнего периода, причем на непо­гашенный остаток будут начисляться сложные проценты по процентной ставке 20% гйдовых. По какой цене кредитор может продать этот контракт байку, который на ссуженные деньги на­числяет сложные процента по процентной ставке 25% годовых?