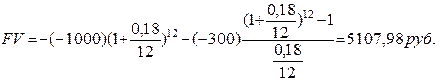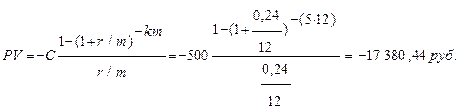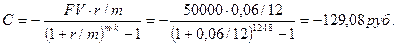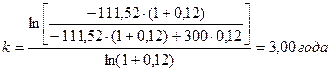Уравнение эквивалентности в общем виде
В первой главе мы вывели уравнение эквивалентности (1.6) между одноразовым взносом и накопленной к концу срока финансовой сделки суммой FV при условии наращивания процентов по номинальной ставке r. В этом уравнении не учитывались периодические платежи С. В разделе 2.2.2 выведено уравнение эквивалентности (2.4), связывающее периодические платежи С и накопленную сумму FV при условии, что не было первоначального взноса PV.
В повседневных финансовых операциях накопления денег, кредитования, аннуитета (см. раздел 2.1) фигурируют как первоначальные, так и периодические взносы.
Все эти ситуации описываются общим эквивалентным уравнением, объединяющим уравнения (1.6) и (2.4)
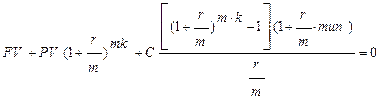(2.5)
Из этого уравнения можно определить одну из величин как функцию остальных:
1. FV=f(PV,С,r,m,k) – будущую сумму в любой момент;
2. PV=f(FV,С,r,m,k) – текущую сумму, пересчитанную к любому моменту финансовой сделки;
3. С=f(PV,FV,r,m,k) – выплаты;
4. k=f(PV,FV,С,r,m) – срок договора;
5. r=f(PV,FV,С,m,k) – норму, годовую процентную ставку.
Определение будущей суммы
Пример 2.2 Изменим условия примера 2.1. Пусть в начале срока вложена сумма PV=1000 руб. Ежемесячно вносится еще по 300 руб. Годовая процентная ставка 18%. Как при этом изменятся суммы в конце года постнумерандо и пренумерандо.
|
Решение PV=-1000 руб.
с=-300 руб.
r=0,18
k=1
m=12
 |
FV=?
2) Взносы пренумерандо.
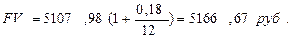
Определение текущей суммы
Из уравнения (2.5) получим в общем виде
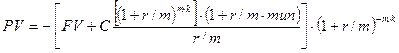. (2.6)
Откуда
(2.7)
Пример 2.3. Пенсионер получил наследство и хотел бы заключить договор с пенсионным фондом с условием получения 500 руб. в конце (начале) каждого месяца на протяжении 5 лет. Какая сумма обеспечит получение такого дохода при процентной ставке 24% годовых?
|
Решение. FV=0
С=500
r=0,24
k=5
m=12
 |
PV=?
2) Выплаты в начале месяца (тип=1)
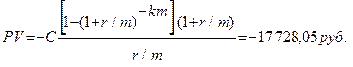
Как видим, во втором случае вклад должен быть значительнее почти на 350 руб. Знак минус показывает, что первоначальную сумму PV нужно отдать в банк.
Сколько денег пришлось бы пенсионеру положить в шкатулку, чтобы вынимать из нее по 500 руб. ежемесячно в течение 5 лет?
PV=500·12·5=30000 руб.
В обоих случаях банк за счет процентов доплачивает больше 12000 руб.
Определение периодических выплат
Какую сумму С нужно вносить регулярно в начале (в конце) периода, чтобы при первоначальном взносе PV и годовой процентной ставке r через n=m·k периодов накопить капитал FV? Из (2.5) имеем
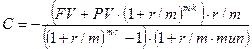. (2.8)
Пример 2.4 Родители решили накопить за 18 лет на образование ребенка 50000 руб. Банк обеспечивает 6% годовых по вкладу. Сколько денег нужно вносить в конце каждого месяца?
|
FV=50000 руб.
PV=0
|
k=18
m=12
 |
С=?
Расчет срока ренты
При разработке условий контракта иногда возникает необходимость в определении срока ренты. Решая уравнение (2.5) относительно числа лет k, получим
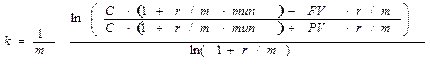(2.9)
Пример 2.5 Фирме нужно выплатить долг 300 млн. руб. ежегодными платежами по 111,52 млн. руб. Процентная ставка согласно договору между кредитором и фирмой установлена 12% годовых. Нужно определить срок платежа.
|
Решение PV=300 млн. руб.
FV=0
С=-111,52 млн. руб.
r=0,12
m=1
тип=1
 |
k=?
За это время с учетом процентов фирма выплатит сумму
S=-111,52·3=-334,56 млн. руб.
Переплата по процентам составит 34,56 млн. руб.
Пример 2.6 Акционерное общество решило создать резервный фонд в размере 600 млн. руб. Взносы в размере 66,834 млн. руб. вносятся в конце каждого года под годовую процентную ставку 16%. Сколько времени будет формироваться фонд?
Решение.
|
PV=0 FV=600 млн. руб.
C=-66,834 млн. руб.
r=0,16
m=1
тип=0
 |
k=?