Типовые примерыи методы их решения
Пример1.7.1. Дана следующая (условная) схема налога на проценты:
8% с части дохода от 0 тыс. руб. до 5 тыс. руб.; 12% с части дохода от 5 тыс. руб. до 20 тыс. руб.; 16% с части дохода от 20 тыс. руб. до 40 тыс. руб.;
22% с части дохода от 40 тыс. руб. и выше.
Предприниматель получил в качестве начисленных процентов сумму 41 тыс. руб. Какой налог он должен уплатить? Чему равна в этом случае средняя ставка налога?
Решение. Разобьем 41 тыс. руб. на части, соответствующие предельным ставкам налога: 41 = 5 + 15 + 20 + 1. Следовательно, общая величина налога на проценты составит:
5 *0,08+15 *0.12+20 *0.1б + 1 *0,22 = 5,62 тыс. руб.
Для определения средней ставки налога поделим полученную величину на 41 тыс. руб.:
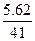 = 0.13707, или 13,707%.
= 0.13707, или 13,707%.
Таким образом, если бы ставка налога на проценты была неизменной и равной 13,707%, то величина налога на сумму 41 тыс. руб. составила бы 5,62 тыс. руб.
Средняя ставка показывает общее влияние налогов, однако предельная ставка более четко отражает ситуацию. Так, если бы величина начисленных процентов возросла бы с 41 тыс. руб. до 61 тыс. руб., то размер налога увеличился бы согласно предельной ставке 22% на сумму 20 * 0,22 =4,4 тыс. руб., а не на сумму 20*0.13707 = 2,7414 тыс. руб. в соответствии со средней ставкой.
Пример 1.7.2.Для участия в некотором проекте предпринимателю понадобится 28 тыс. руб. Между тем он располагает лишь 25 тыс. руб. С целью накопления требуемой суммы предприниматель собирается положить в банк 25 тыс. руб. Предлагаемая банком процентная ставка равна 40% годовых. Какое количество дней необходимо для накопления требуемой суммы с учетом уплаты налога на проценты, если банк начисляет простые проценты, используя в расчетах точные проценты и точное число дней, а ставка налога на проценты равна 12%? Год невисокосный. Какое будет количество дней, если налог на проценты не надо уплачивать?
Решение.Обозначим через t необходимое число дней, тогда, полагая в формуле (37) Р - 25 тыс. руб., Fq = 28 тыс. руб., п = t/365 года, r = 0,4, q = ОД2, получим уравнение относительно переменной t:
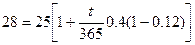
Решая это линейное уравнение, находим: t = 124,43 дня. Таким образом, 125 дней будет вполне достаточно для достижения требуемой суммы.
Бели бы не было налога на проценты, то, либо решая уравнение 28 = 25-(1 + 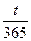 0,4), получающееся из формулы (10), либо пользуясь непосредственно формулой (21), получим:
0,4), получающееся из формулы (10), либо пользуясь непосредственно формулой (21), получим:
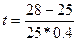 365=109,5 дня.
365=109,5 дня.
Следовательно, необходимость уплаты налога на проценты увеличивает искомый срок на 15 дней. Вообще, как видно из формулы (37), налог на проценты по существу уменьшает ставку наращения: начисление процентов фактически происходит не поставке 0,4, а по ставке 0,4(1-0.12) = 0,352, т.е. по процентной ставке 35,2% годовых, которая меньше 40%.
Заметим, что, обозначая n = 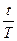 и разрешая формулу (37) относительно t, получим формулу, аналогичную (21):
и разрешая формулу (37) относительно t, получим формулу, аналогичную (21):
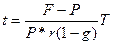
которой можно воспользоваться при ответе на первый вопрос примера и которая при q = 0 совпадает с формулой (21).
Пример 1.7.3.На депозит была помещена сумма в 20 тыс. руб. на 240 дней под простую учетную ставку 30% годовых. Определите наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты равна 12% и начисляются обыкновенные проценты. Если в условиях примера наращение осуществлялось по годовой процентной ставке 30%, то какова будет наращенная сумма после уплаты налога на проценты?
Решение.Пользуемся формулой (38), где Р = 20 тыс. руб.,
 года d=0.3 g =0.12
года d=0.3 g =0.12
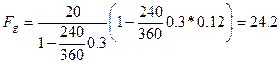 тыс.руб
тыс.руб
Без уплаты налога наращенная сумма равнялась бы (по формуле (20)) 25 тыс. руб. Формула (38) показывает, что государство как бы учитывает сумму 25 тыс. руб. за 240 дней по простой учетной ставке 0,3 • 0.12 = 0,036, что равносильно 3,6% годовых.
Если наращение осуществлялось по простой процентной ставке 30% годовых, то по формуле (37):
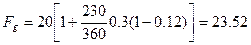 тыс.руб
тыс.руб
Пример 1.7.4.Клиент положил в банк 60 тыс. руб. под простую процентную ставку 40% годовых и через полгода с учетом уплаты налога на проценты получил 70,2 тыс. руб. Определите ставку налога на проценты.
Решение.Пусть 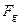 =70.2 тыс. руб., Р = 60 тыс. руб., n=0,5 года, r = 0,4. Разрешая формулу (37) относительно q, получим:
=70.2 тыс. руб., Р = 60 тыс. руб., n=0,5 года, r = 0,4. Разрешая формулу (37) относительно q, получим:
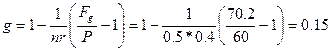
что эквивалентно q = 15 %.
Задачи
1.7.1. Дала следующая (условная) схема налога на проценты: 9% с части дохода от 0 тыс. руб. до 10 тыс. руб.;
13% с части дохода от 10 тыс. руб. до 25 тыс. руб.;
18% с части дохода от 25 тыс. руб. до 38 тыс. руб.;
26% с части дохода от 38 тыс. руб. и выше.
Предприниматель получил в качестве начисленных процентов сумму: а) 37,9 тыс. руб.; б) 38,1 тыс. руб. Какой налог он должен уплатить? Чему равна средняя ставка налога?
1.7.2. На депозит была помещена сумма в размере 8 тыс. руб. под 20% годовых на 15 месяцев на условиях однократного начисления простых обыкновенных процентов. Определите наращенную
сумму с учетом уплаты налога на проценты, если ставка налога на проценты равна 12%.
1.7.3. Клиент банка поместил деньги на депозит под простую процентную ставку и через год получил с учетом уплаты налога на проценты 860 руб. Какая сумма была помещена на депозит, если индекс роста ее за это время без учета уплаты налога на процевты составил 1,38 и ставка налога на проценты равна 12%?
1.7.4. В результате использования простой процентной ставки индекс роста вклада за год составил 1,215. На сколько процентов за это время увеличился вклад с учетом уплаты налога на проценты, если ставка налога на проценты равна 14%?
1.7.5. На депозит была помещена сумма в размере 6 тыс. руб. на полтора года, по истечении которых на сумму были начислены простые проценты по годовой учетной ставке 16%. Определите наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты равна 12%.
1.7.6. На какой срок необходимо поместить имеющуюся денежную сумму на условиях однократного начисления (по истечения срока) простых процентов по процентной ставке 35% годовых, чтобы она с учетом уплаты налога на проценты увеличилась в 2 раза, если ставка налога равна 20%? Как изменится ответ при осуществлении наращения по простой учетной ставке?
1.7.7. На какой срок необходимо поместить имеющуюся денежную сумму на условиях однократного начисления (по истечении срока) простых процентов по процентной ставке 40% годовых, чтобы начисленные проценты с учетом уплаты налога на процевты были в 1,6 раза больше первоначальной суммы, если ставка налога на проценты равна 15%? Как изменится ответ при осуществлении наращения по простой учетной ставке?
1.7.8. Вклад 50 тыс. руб. был размещен в банке 10 февраля под простую процентную ставку 35% годовых и востребован 14 декабря того же года. После уплаты налога на проценты вкладчик стал обладателем суммы в размере 63,133 тыс. руб. Какой способ начисления процентов использовал банк, если ставка налога на проценты равна 12%? Год невисокосный.
1.7.9. Простая процентная ставка по вкладам до востребования, составляющая в начале года 28% годовых, через полгода была увеличена до 35%, а еще через квартал - до 40% годовых. Определите наращенную за год сумму с учетом уплаты налогана проценты, если ставка налога на проценты равна 15%, величина вклада - 12 тыс. руб. и обыкновенные проценты начисляются в конце года.
1.7.10. За какой срок вклад 8 тыс. руб. возрастет до 9 тыс. руб. с учетом уплаты налога на проценты при однократном начислении (по истечении срока) процентов по простой процентной ставке 34% годовых, если ставка налога на проценты равна 12%?
1.7.11. Для участия в некотором проекте предпринимателю понадобится 12 тыс. руб. Между тем он располагает лишь 10 тыс. руб. С целью накопления требуемой суммы предприниматель собирается положить в банк 10 тыс. руб. Предлагаемая банком процентная ставка равна 35% годовых. Какое количество дней необходимо для накопления требуемой суммы с учетом уплаты налога на проценты, если банк начисляет простые проценты, используя в расчетах точные проценты и точное число дней, а ставка налога на проценты равна 12%? Каково необходимое количество дней, если налог на проценты не надо уплачивать? Год високосный.
1.7.12. Какую сумму необходимо положить в банк под процентную ставку 30% годовых с начислением простых процентов по истечении года, чтобы с учетом уплаты налога на проценты можно было бы получать ежегодную ренту в размере 600 руб., а сумма на счете в банке оставалась бы неизменной? Ставка налога на проценты равна 20%.
1.7.13. Какую сумму необходимо поместить в банк под простую процентную ставку 36% годовых на условиях однократного начисления процентов в конце срока помещения денег, чтобы накопить с учетом уплаты налога на проценты 20 тыс. руб.: а) за полгода; б) за 2 года, если ставка налога на проценты равна 15%7
1.7.14. Клиент собирается поместить в банк 2000 долл. на рублевом депозите сроком на полгода под 58% годовых. Курс покупки долларов на начало срока - 15 руб.40 коп., ожидаемый курс продажи через полгода - 18 руб. 70 коп. Процентная ставка при долларовом депозите - 24%. При любом депозите простые проценты начисляются по истечении срока. Найдите наращенную сумму: а) при конвертации валюты; б) непосредственно на валютном депозите с учетом уплаты налога на проценты, если ставка налога на проценты равна 12%.
1.7.15. Господин N 1 июля 1998 г. поместил 12 тыс. руб. на трехмесячный депозит под простую процентную ставку 34% годовых. По рублевому депозиту начислялись точные проценты с точным числом дней, ставка налога на проценты равна 12%. На сколько больше рублей получил бы господин N, если бы он на все деньги приобрел доллары США, а 1 октября обменял доллары на рубли? Банк 1 июля продавал доллары США по курсу 6 руб. 20 коп. за доллар, а 1 октября покупал доллары США по курсу 14 руб. 10 коп. за доллар, и комиссионные при обмене валюты не взимались.
1.7.16. Вкладчик, владея 18 тыс. руб., хочет получить, положив деньги на депозит, через полгода не менее 20 тыс. руб. Определите требуемую простую годовую процентную ставку, на основании которой вкладчик должен выбрать банк, если ставка налога на проценты равна 15%,
1.7.17. Положив в банк 50 тыс. руб. под простую процентную ставку 42% годовых, предприниматель через 9 месяцев получил с учетом уплаты налога на проценты 62,6 тыс. руб. Определите ставку налога на проценты.
1.7.18. Клиент поместил 25 тыс. руб. в банк под простую процентную ставку 34% годовых сроком на 3 месяца. Определите доходность такой сделки для клиента в виде простой годовой процентной ставки, если ставка налога на проценты равна 15%. Зависит ли эта доходность от величины помещенной суммы?
Инфляция
Основные положении
• Инфляция представляет собой процесс, характеризующийся повышением общего уровня цен в экономике или, что ирак-тическн эквивалентно, снижением покупательной способности денег. При этом инфляция может проявляться двояко: во-первых, в переполнении сферы обращения бумажными деньга-ми вследствие их чрезмерного выпуска; во-вторых, в сокращении товарной массы в обращении при неизменном количестве выпущенных денег. Основополагающим сущностным признаком инфляции является рост цен в среднем. • Темпы инфляции определяются с помощью системы ин дексов цен - относительных показателей, характеризующи; среднее изменение уровня цен некоторого фиксированного набора товаров и услуг за выбранный период.
• Индекс цен (его также называют индексом инфляции) показывает, во сколько раз выросли цены за рассматриваемый период. Наиболее широко используемым индексом цен является индекс потребительских цен, отражающий рост цен на некоторый постоянный потребительский набор товаров и услуг (такой набор часто называют потребительской корзиной).
• Темп инфляции, выраженный в процентах, показывает, на сколько процентов выросли цены за рассматриваемый период. Вместо выражения "темп инфляции" часто используют термин '-'уровень инфляции" или просто говорят "инфляция", подразумевая именно ее темп за данный промежуток времени.
• Для того чтобы в условиях инфляции стоимость первоначального капитала при его наращении на самом деле росла, исходную процентную ставку увеличивают - происходит ее индексация.
• При инфляции различают следующие виды процентных ставок. Номинальная процентная ставка - это исходная базовая (как правило, годовая) процентная ставка, указываемая в договорах. Доходность, выражаемая этой ставкой, не скорректирована на инфляцию. Номинальная ставка говорит об абсолютном увеличении денежных средств инвестора. Реальная процентная ставка показывает доходность с учетом инфляции, характеризующейся снижением покупательной способности денег. Реальная ставка говорит о приросте покупательной способности средств инвестора. Реальная процентная ставка в условиях инфляции всегда меньше номинальной и может быть даже отрицательной. Положительная процентная ставка - это любая ставка, при которой будет происходить реальное увеличение стоимости капитала при данном индексе инфляции. Иногда любую процентную ставку, превышающую номинальную, называют брут-то-ставкой процента. Но, как правило, брутто-ставка является положительной процентной ставкой.
• Дефляция представляет собой процесс, характеризующийся снижением общего уровня цея в экономике.
Вопросы для обсуждения
1. Что представляет собой инфляция?
2. Каким образом могут проявляться инфляционные процессы?
3. Что называется индексом цен и что он показывает? В каких единицах измеряется? Как еще называется индекс цен?
4. Что такое индекс потребительских цен?
5. Как определяется и что характеризует темп инфляции?
6. Какая существует связь между индексом цен и темпом инфляции за рассматриваемый период?
7. Всегда ли повышение цены товара является результатом только инфляционных процессов?
8. Могут ли при высоком уровне инфляции цены на некоторые товары оставаться стабильными или даже падать?
9. Возможна ли инфляция при отсутствии денег?
10. Если текущий темп инфляции отличается от ожидаемого, то в каком случае оказывается в выигрыше кредитор, а в каком -должник?
11. Если известны индексы инфляции за каждый из нескольких периодов, расположенных последовательно друг за другом, то каким образом определить индекс инфляции сразу за эти несколько периодов?
12. Как связан среднемесячный темп инфляции с годовым индексом инфляции?
13. В первом году инфляция составила 200%, в следующем году индекс инфляции был равен 2. Во сколько раз выросли цены за эти два года?
14. Можно ли утверждать, что при среднемесячном темпе инфляции в 2% годовой темп инфляции будет 24%?
15. Как определяется изменение реальной покупательной способности денег за некоторый период при известном индексе инфляции за этот период?
16. При каком соотношении между множителем наращения и индексом инфляции будет происходить реальное наращение капитала?
17. Что понимается под эрозией капитала?
18. Какая должна быть в условиях инфляции простая процентная ставка по кредитам, чтобы взятая сумма с точки зрения ее покупательной способности оставалась постоянной? 19. Какая ставка называется положительной процентной ставкой?
20. Для каких целей в условиях инфляции осуществляют индексацию ставки?
21. Каким образом в условиях инфляции можно индексировать банковские вклады?
22. Почему в условиях инфляции необходимо различать номинальную и реальную процентные ставки?
23. Можно ли сказать, что номинальная процентная ставка представляет собой выраженное в процентах увеличение денежной суммы, которую получает кредитор от заемщика?
24. Можно ли сказать, что реальная процентная ставка представляет собой выраженное в процентах увеличение покупательной способности, которое получает кредитор от заемщика?
25. Может ли реальная процентная ставка быть отрицательной?
26. Может ли 1000% годовых быть отрицательной процентной ставкой?
27. Перечислите виды процентных ставок, которые различают в условиях инфляции.
28. Является ли эффективной финансовая сделка при большой инфляции?
29. Чем характеризуется процесс дефляции?
30. Как изменится за два года индекс потребительских цен, если в первый год дефляция составила 10%, а во втором году инфляция равнялась 10%?
