Типовые примеры и методы их решения 4 страница

Пример 2.2.12. Вклад в размере 20 тыс. руб. помещен в банк сроком на 5 лет, причем предусмотрен следующий порядок на­числения сложных процентов по плавающей годовой учетной ставке: в первые два года - 16%, в последующие два года - 19% и в оставшийся год - 23%. Найдите наращенную сумму. При использовании какой постоянной сложной учетной ставки мож­но получить такую же наращенную сумму?

Решение.Наращенную сумму за первые два года опредсля-

20 ем по формуле (76), где F_n =20, n =2, d = 0,16: 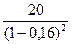тыс.руб. Наращенную сумму за следующие два года определяем также по формуле (76), где F_n= 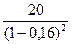, n =2, d = 0,19:

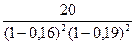= тыс. руб. Аналогичным образом поступая с последним годом, когда d = 0,23 , находим, что через 5 лет нара­щенная сумма составит:

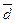P= = 56,106 тыс. руб. Годовую (постоянную) учетную ставку , обеспечивающую такой же результат, как и плавающая ставка, можно найти из

равенства (1- 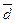)⁵ = (1-0,16)²(1-0,19)²(1-0,23), разрешая его от­носительно :

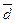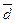=1- 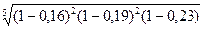=0,1864, или 18,64%.

Пример 2.2.13.Банк выдал кредит сроком на 1 месяц под 3% за месяц, удержав проценты при выдаче кредита. Определи­те доходность такой финансовой сделки для банка в виде годо­вой эффективной процентной ставки и поясните, как такого ро­да сделку можно соотнести с начислением сложных процентов по учетной ставке.

Решение.Обозначим через F величину кредита, тогда за­емщику выдается сумма F -0.03F = 0,97F. Теперь можно вос­пользоваться формулой (64), где P = 0,97F, F_n =F и n = 1/12:

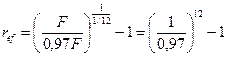= 0,4412, или 44Д2%.

Записывая формулу для вычисления r_ef в виде:

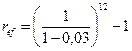
делаем вывод, что начисление процентов один раз за год по процентной ставке 44,12% обеспечивает такой же результат, как и начисление ежемесячно процентов по годовой номинальной

учетной ставке d⁽¹²⁾ =3%*12 = 36%.

Таким образом, выдача банком кредита с одновременным удержанием начисленных процентов по существу означает, что на выданную сумму будут начисляться сложные проценты по учетной ставке.

Пример 2.2.14.Согласно финансовому соглашению банк начисляет по полугодиям проценты на вклады по сложной учет­ной ставке 28% годовых. Определите в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их размещении: а) на 3 месяца; б) на год.

Решение,а) Стоимость привлеченных средств найдем по формуле (23), где через Р обозначена использованная сумма средств; через F-P - проценты, выплаченные за использова­ние суммы Р в течение времени п, a F определяется с помо­щью формулы (77), где n = 0,25, т = 2, d⁽²⁾ = 0,28 . Итак,

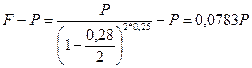
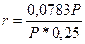= 0,3132, или 31,32% годовых.

Естественно, можно было и сразу применить формулу (85):

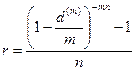устанавливающую эквивалентность простой ставки r и сложной учетной ставки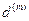

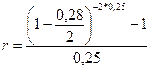= 03132.

б) Полагая n = 1, воспользуемся сразу формулой (85) экви­валентности простой процентной и сложной учетной ставок:

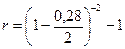= 0,3521 = 35,21%.

Заметим, что если найти простую учетную ставку, эквива­лентную простой процентной ставке r = 35,21%, то она в точности будет равна годовой эффективной учетной ставке, соответст­вующей номинальной учетной ставке d 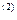= 28%. Действительно, по формуле

а по формуле (74) получаем то же значение:

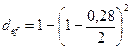=0,2604.

Пример 2.2.15. Вексель учитывается в банке за 3 года до его погашения по сложной учетной ставке 26% годовых. Найдите доходность такой финансовой операции для банка в виде эф­фективной учетной ставки, если банк удерживает комиссионные в размере 2% от суммы, выплачиваемой за вексель. Как изме­нится такого рода доходность при учете за 2 года и за 6 лет до срока погашения?

Решение. Пусть за 3 года до срока погашения предъявлен вексель на некоторую сумму Fз. Так как сумма, выплачиваемая

за вексель, составит: F₃ (1-0,26) 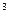= 0,4052Fз, то величину удер­живаемых комиссионных определяем, взяв 2% от этой суммы: 0,4052 Fз* 0,02 = 0,0081 Fз. Следовательно, векселедержатель полу­чит сумму: P = 0,4052F₃-0,0081F₃ =0,3971F₃ . Теперь по формуле (75) можно определить доходность финансовой операции для банка в виде эффективной учетной ставки:

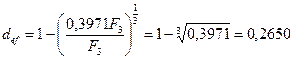
т.е. d_ef = 26,50%, что больше объявленных банком 26% годовых.

Таким образом, удержание комиссионных увеличивает доход­ность финансовой операции для банка.

При предъявлении векселя за 2 года до срока сумма, выплачи­ваемая за вексель, составит: F₂(l-0,26)² =0,5476 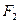, ^и поэтому по­сле удержания комиссионных векселедержатель получит сумму:

P = 0,5476 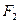- 05476 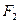* 0,02 = 0,5366F₂ ,

и, следовательно, доходность для банка составит:

т.е. больше, чем при учете за 3 года.

Аналогичным образом при учете за 6 лет получим:

P=F 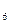(1 - 0,26)⁶ - F₆ (1 - 0.26)⁶ * 0,02 = 0,1609F₆,

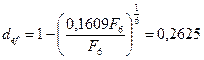
т.е. меньше, чем при учете за 3 года.

Основываясь на рассмотренном примере, можно сделать вы­вод, что при удержании комиссионных увеличение срока, за ко­торый происходит учет по сложной учетной ставке, уменьшает доходность в виде эффективной учетной ставки для банка. Ко­нечно, если комиссионные не взимаются, то при учете за любое время до срока погашения по сложной учетной ставке доход­ность такой финансовой сделки в виде годовой эффективной учетной ставки будет постоянна и равна 26%.

Пример 2.2.16. Предприятие приобрело универсальный ста­нок за 320 тыс. руб. Срок службы станка - 8 лет, после чего он реализуется по остаточной стоимости 50 тыс. руб. Используя способ фиксированного процента, составьте таблицу уменьше­ния стоимости станка по годам.

Решение. В соответствии со способом фиксированного процента стоимость имущества снижается к концу каждого года на одно и то же число процентов d от его стоимости на начало года. Обозначим через Р первоначальную стоимость станка, Р_п - остаточную стоимость станка через л лет и полу­чим формулу для определения стоимости станка на конец k -го года.

В конце первого года первоначальная стоимость станка Р бу­дет уменьшена иа величину Pd и станет равна Р -Pd = P(1 - d). В

конце второго года стоимость Р(1 - d) будет уменьшена на вели­чину P(1- d)d и станет равна P(1-d)-P(1-d)d = P(1-d)². Про­должая аналогичным образом рассуждения, найдем, что в конце k -го года стоимость станка будет равна Р(1 – d) 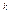(т.е. сумма Р учитывается за к лет по сложной учетной ставке d ).

Поскольку в конце п -го года остаточная стоимость станка равна 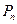то получим равенство 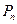= Р(1 – d) 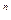, из которого можно определить фиксированный процент d снижения стоймости станка: d = 1 - 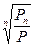(очевидно, эта формула не случайно

напоминает формулу (75) определения эффективной годовой учетной ставки). В данном случае срок службы станка составля­ет n = 8 лет, Р = 320 тыс. руб., 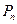- 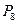= 50 тыс. руб., поэтому:

d=1- 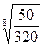= 0,2071, или 20,71%.

Далее последовательно находим амортизационные отчисле­ния за год и стоимость станка на конец этого года:

а) в конце первого года:

Pd = 320 * 0,2071 = 66,272 тыс. руб.,

Р - Pd = 320 - 66,272 = 253,728 тыс. руб.;

б) в конце второго года:

Р(1 -d)d = 253,728 * 0,2071 - 52,547 тыс. руб.,

P(1-d)² = 253,728-52,547 =201,181тыс. руб.

Продолжая аналогичным образом, получим таблицу:

Год службы	Амортизации иные отчисления за год, тыс. руб.	Стоимость на конец года, тыс. руб.
	66,272	253,728
	52,547	201,181
	41,665	159,516
	33,036	126,48
	26,194	100,286
	20,769	79,517
	16,468	63,049
	13,057	49,992

Небольшое отличие остаточной стоимости от 50 тыс. руб. , (получили 49,992 тыс. руб.) связано с погрешностью прибли-.

женных вычислении.

Задачи

2.2.1. Вексель яа сумму 100 тыс. руб. учитывается за 4 года до срока погашения. Составьте схему учета векселя по годам, если при этом используется сложная учетная ставка 20% годо­вых. Какую сумму получит предъявитель векселя?

2.2.2. Долговое обязательство на выплату 12 тыс. руб. со сроком погашения через 5 лет учтено за 3 года до срока с дис­контом по сложной учетной ставке 14% годовых. Найдите вели­чину дисконта. Как изменится величина дисконта, если долговое обязательство учтено сразу после его выдачи?

2.2.3. Сделайте сравнительный анализ графиков, отражающих дисконтирование по простой и по сложной учетным ставкам.

2.2.4. Определите дисконтированную сумму при учете 1 тыс. руб. по простой и сложной учетным ставкам, если годовая учет­ная ставка равна 18% и учет происходит за 30 дней, 210 дней, 1 год, 3 года, 5 лет, 20 лет. Полагать год равным 360 дней. Обсу­дите полученные результаты.

2.2.5. Вексель на сумму 50 тыс. руб. со сроком погашения через 3 года учтен за 26 месяцев по сложной учетной ставке 20% годовых. Определите суммы, которые получит предъявитель векселя при различных способах учета векселя (при применении только сложной учетной ставки и при применении смешанной схемы).

2.2.6. В банк 10 июня предъявлен для учета вексель на сумму 15 тыс. руб. со сроком погашения 10 сентября того же года. Банк учитывает вексель по сложной учетной ставке 20% годовых, счи­тая год равным 360 дням и проводя приблизительный подсчет дней. Определите сумму, которую получит векселедержатель от банка, и комиссионные, удерживаемые банком в свою пользу за предоставленную услугу. Как изменятся результаты, если срок погашения векселя - 10 сентября следующего года?

2.2.7. За 3 года 9 месяцев до срока погашения в банк предъяв­лен вексель на сумму 80 тыс. руб. Банк согласился учесть вексель по сложной учетной ставке 24% годовых при осуществлении дисконтирования раз в год и выплатил предъявителю векселя 28,797 тыс. руб. Какую из двух схем дисконтирования (только по сложной, учетной ставке или смешанную) использовал банк? 2.2.8. Вексель на сумму 30 тыс. руб. учтен за 15 месяцев до срока погашения по номинальной учетной ставке 16% годовых, причем производилось поквартальное дисконтирование. Составь­те схему учета по кварталам. Какую сумму получит векселедер­жатель?

2.2.9. Долговое обязательство на выплату 200 тыс. руб. со сроком погашения через 6 лет учтено за три года до срока. Опредслите полученную сумму, если производилось: а) полугодо­вое; б) поквартальное; в) помесячное дисконтирование по номи­нальной учетной ставке 18% годовых.

2.2.10. Определите современное значение суммы в 30 тыс. руб., если она будет выплачена через 4 года 9 месяцев и дискон­тирование производится по полугодиям по номинальной годо­вой учетной ставке 20%.

2.2.11. Определите, какую сумму получит владелец векселя на 40 тыс. руб. со сроком погашения через 26, месяцев, если он учтет вексель сразу при его выдаче по номинальной учетной ставке 24% годовых при осуществлении операции дисконтиро­вания 4 раза в год. Сравните два способа дисконтирования (при применении только сложной учетной ставки и при применении смешанной схемы).

2.2.12. За долговое обязательство 50 тыс. руб. банком было выплачено 40 тыс. руб. За какое время до срока погашения было учтено это обязательство, если банком использовалась: а) годо­вая сложная учетная ставка 22%; б) годовая простая учетная ставка 22%? Полагать в году 360 дней.

2.2.13. Вексель был учтен за 21 месяц до срока погашения, при этом владелец векселя получил 0,8 от написанной на вексе­ле суммы. По какой сложной годовой учетной ставке был учтен этот вексель?

2.2.14. За учтенный вексель была выплачена половина от на­писанной на векселе суммы. За какое время до срока погашения был учтен вексель при дисконтировании по простой и по слож­ной учетным ставкам, если годовая учетная ставка равна: а) 5%; б) 10%; в) 25%; г) 50%; д) 80%?

2.2.15. Вы имеете вексель на сумму 15 тыс. руб. и хотели бы при его учете по сложной учетной ставке за 2 года до срока по­гашения получить две трети этой суммы. Какая должна быть годовая номинальная учетная ставка при дисконтировании по­квартально? Как изменится ответ, если дисконтирование осуще­ствляется раз в год?

2.2.16. Долговое обязательство было учтено по номинальной учетной ставке 32% годовых, причем проводилось полугодовое дисконтирование. За какое время до срока погашения было учтено обязательство, если его дисконтированная сумма составила треть от суммы, которую нужно выплатить по этому обязательству?

2.2.17.3а какое время до срока погашения был учтен вексель на сумму 50 тыс. руб., если предъявитель векселя получил 30 тыс. руб. и дисконтирование по номинальной учетной ставке 24% годовых производилось: а) поквартально; б) помесячно?

2.2.18; Долговое обязательство было учтено за 2 года до срока погашения, при этом его владелец получил половину от написан­ной в нем суммы. По какой годовой номинальной учетной ставке было учтено это Обязательство, если производилось: а) полугодо­вое дисконтирование; б) поквартальное дисконтирование?

2.2.19. Какие условия учета при дисконтировании по слож­ной учетной ставке более выгодны банку: а) 32% годовых, полу­годовое дисконтирование; б) 33% годовых, поквартальное дис­контирование?

2.2.20. Вы имеете возможность учесть вексель либо по слож­ной учетной ставке 28% годовых с поквартальным дисконтирова­нием, либо по сложной учетной ставке 29% годовых с помесяч­ным дисконтированием. Какой вариант предпочтительнее?

2.2.21. Рассчитайте эффективную годовую учетную ставку при различной частоте начисления дисконта и номинальной учетной ставке, равной 24% годовых. Сравните между собой полученные результаты.

2.2.22. Долговое обязательство, равное 15 тыс. руб., со сро­ком погашения через 3 года было сразу же учтено в банке, и владелец обязательства получил 10 тыс. руб. Найдите эффек­тивную годовую учетную ставку в этой сделке.

2.2.23. Долговое обязательство на сумму 16 тыс. руб. было уч­тено за 170 дней до срока погашения, и владелец обязательства получил 14 тыс. руб. Определите доходность этой операции в виде эффективной учетной ставки на базе: а) 360 дней; б) 365 дней.

2.2.24. Определите номинальную учетную ставку, если эффек­тивная годовая учетная ставка равна 22% и дисконтирование по сложной учетной ставке осуществляется: а) поквартально; б) поме-

. сячно. 2.2.25. На какую сумму должен быть выписан вексель, чтобы при его учете за 3 года до срока погашения по сложной учетной ставке 28% годовых можно было получить 18 тыс. руб., если дис­контирование производится: а) по полугодиям; б) помесячно? Чему равен дисконт?

2.2.26. За 4 года до срока погашения учтено долговое обяза­тельство, и его владелец получил 5 тыс. руб. Определите сумму, написанную в долговом обязательстве, если учет осуществлялся по сложной учетной ставке и дисконтирование производилось:

а) по полугодиям по учетной ставке 40% годовых; б) помесячно по учетной ставке 30% годовых.

2.2.27. Какая сумма должна быть написана на векселе, чтобы при его учете по сложной учетной ставке 30% годовых было получено 20 тыс. руб., если учет осуществляется: а) за 5 лет до срока погашения при дисконтировании раз в год; б) за 3 года до срока погашения при поквартальном дисконтировании?

2.2.28. В банке за 3 года 8 месяцев до срока погашения был учтен вексель по сложной учетной ставке 35% годовых, и вексе­ледержатель получил сумму в размере 8,422 тыс. руб. Опреде­лите, какую сумму получил бы в этом банке владелец векселя при его учете за 2 года 5 месяцев до срока погашения, если банк использует при дисконтировании смешанную схему.

2.2.29. Определите, время, за которое происходит удвоение первоначальной суммы при начислении простых и сложных про­центов, если используемая учетная ставка равна: а) 5%; б) 10%; в) 15%; г) 25%; д) 50%; е) 75%.

2.2.30. По условиям финансового контракта на депозит 30 тыс. руб., положенный в банк на 4 года, начисляются проценты по сложной учетной ставке 12% годовых. Определите наращенную сумму, если начисление процентов производится: а) ежегодно;

б) ежеквартально; в) ежемесячно. Сравните полученные величины с результатами наращения сложными процентами по процентной ставке 12% годовых.

2.2.31. Что выгоднее: получить 23,5 тыс. руб. через 5 лет или 30,5 тыс. руб. через 6 лет, если можно поместить деньги в банк под сложную учетную ставку 32% годовых? Оцените ситуацию с позиции будущего и с позиции настоящего.

2.232. Сроком на 6 лет выпущена облигация номиналом 1000 руб., причем предусмотрен следующий порядок начисле­ния сложных процентов по плавающей годовой учетной ставке:

в первые три года - 12% годовых, в последующие два года -16% годовых и в оставшийся год - 18% годовых. Найдите нара­щенную сумму. При использовании какой постоянной сложной учетной ставки можно получить такую же наращенную сумму?

2.2.33. Банк выдал кредит сроком на 1 квартал под 8% за квартал, удержав проценты при выдаче кредита. Определите доходность такой финансовой сделки для банка в виде годовой эффективной процентной ставки и поясните, как такого рода сделку можно соотнести с начислением сложных процентов по учетной ставке.

2.2.34. Согласно финансовому соглашению банк начисляет ежеквартально проценты на вклады по сложной учетной ставке 20% годовых. Определите в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их раз­мещении: а) на 3 месяца; б) на 9 месяцев; в) на год.

2.2.35. Вексель учитывается в банке за 2 года до его погаше­ния по сложной учетной ставке 32% годовых. Найдите доход­ность такой финансовой операции для банка в виде эффектив­ной учетной ставки, если банк производит поквартальное дис­контирование и удерживает комиссионные в размере 3% от суммы, выплачиваемой за вексель.

2.2.36. Вексель учитывается в банке за 2 года 6 месяцев до срока погашения по сложной учетной ставке 28% годовых, при­чем дисконтирование проводилось поквартально. При взимании комиссионных с суммы, выплачиваемой за вексель, доходность такой финансовой операции для банка в виде эффективной учетной ставки получилась 29%. Сколько процентов составили комиссионные от суммы, выплачиваемой за вексель?

2.2.37. Вексель учитывается в банке по сложной учетной ставке 30% годовых, при этом дисконтирование производится помесячно и банком взимаются комиссионные в размере 1,5% от суммы, выплачиваемой за вексель. За какое время (в днях) до срока погашения должен учитываться вексель, чтобы доход­ность такой сделки для банка в виде годовой эффективной учет­ной ставки составила 38%? Полагать в году 365 дней.

2.2.38. Некоторая сумма в долларах США обменивается на рубли, после чего помещается на рублевый депозит на 2 года 9 месяцев под учетную ставку 25% годовых с ежегодным начис­лением сложных процентов. Полученная наращенная сумма опять конвертируется в доллары США. Определите доходность такой финансовой операции в виде годовой эффективной учетной ставки, если курс покупки долларов на начало срока - 18 руб. 42 коп., а курс продажи через 2 года 9 месяцев - 22 руб. 30 коп. и начисление процентов осуществлялось: а) по схеме сложных процентов; б) по смешанной схеме.

2.2.39. На валютном (долларовом) депозите наращение осу­ществляется ежеквартально сложными процентами по годовой процентной ставке 24%. На рублевом депозите наращение осу­ществляется ежеквартально сложными процентами по годовой учетной ставке 24%. Курс покупки составляет 20 руб. 15 коп. за 1 долл. США. Какой должен быть курс продажи валюты, чтобы доходность в виде годовой эффективной процентной ставки за два года финансовой операции "конвертирование - наращение -конвертирование" была больше доходности при непосредствен­ном инвестировании валютных средств?

2.2.40. На вклад 40 тыс. руб. по истечении 3 лет были начисле­ны сложные проценты по годовой номинальной учетной ставке 28% исходя из ежеквартальной схемы начисления. После уплаты налога на проценты величина наращенной суммы составила 88,891 тыс. руб. Определите ставку налога на проценты, если налог на все полученные проценты был выплачен один раз в конце срока.

2.2.41. На вклад 50 тыс. руб. в течение 4 лет раз в год начис­лялись сложные проценты по годовой номинальной учетной ставке 28% исходя из полугодовой схемы начисления. После уплаты налога на все начисленные проценты величина итоговой наращенной суммы составила 151,979 тыс. руб. Определите ставку налога на проценты, если налог на проценты уплачивался каждый год путем выделения средств из накапливаемой суммы.

2.2.42. На какой срок необходимо поместить имеющуюся де­нежную сумму под годовую номинальную процентную ставку 30% с однократным начислением в конце срока сложных процен­тов исходя из ежемесячной схемы начисления, чтобы наращенная сумма была в 2,4 раза больше первоначальной суммы с учетом уплаты налога на проценты, если ставка налога на проценты рав­на 15% и налог на все полученные проценты выплачивается один раз в конце срока? Как изменится ответ при осуществлении на­ращения по сложной учетной ставке 30% годовых?

2.2.43. Фирма приобрела оборудование за 950 тыс. руб. Срок службы оборудования - 10 лет, после чего фирма намеревается реализовать изношенное оборудование за 100 тыс. руб. Исполь­зуя способ фиксированного процента, составьте таблицу уменьшения стоимости оборудования по годам.

2.3. Непрерывная ставка

Основные положения

• При анализе сложных финансовых проблем в банковской практике нередко возникает задача начисления сложных про­центов за очень малые промежутки времени. В частности, такая задача особенно актуальна,. когда финансовые операции осуще­ствляются и регистрируются с помощью электронных методов. В такого рода ситуациях говорят о непрерывном начислении процентов и их непрерывной капитализации.

• Предел годовой номинальной процентной, ставки, когда число начислений сложных процентов стремится к бесконечно­сти, а эффективная ставка постоянна, называется силой роста или интенсивностью наращения за год при непрерывном начис­лении процентов. Силу роста также еще называют непрерывной ставкой и, чтобы отличать ее от обычной (дискретной), вводят специальное обозначение - .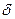

• При непрерывном начислении процентов исчезает разли­чие между антисипативным и декурсивным способами начисле­ния, так как в такой ситуации начало и конец периода перестают отличаться.

• При использовании непрерывной ставки будущие поступ­ления, являющиеся разновременными суммами, можно оцени­вать с позиции любого момента времени.

Вопросы для обсуждения

1. Как пояснить переход к непрерывным процентам?

2. Чем отличаются дискретные проценты от непрерывных?

3. Какая постоянная используется при непрерывном начисле­нии процентов?

4.Какая ставка называется силой роста?

5.Чему равен множитель наращения при непрерывном начис­лении процентов?

6.Можно ли сказать, что сила роста показывает скорость отно­сительного роста накапливаемой суммы?

7.Какое существует соотношение между силой роста и годовой процентной ставкой?

8. Какое существует соотношение между силой роста и годовой учетной ставкой?

9. Укажите приближенные соотношения, связывающие силу роста и годовую процентную ставку.

10.Укажите приближенные соотношения, связывающие силу роста и годовую учетную ставку.

11.В каких случаях сила роста практически совпадает с про­центной и учетной годовыми ставками?

12.Почему исчезает различие между антисипативным и декурсивным способами начисления процентов, если использовать непрерывное начисление?

13.Что такое сила учета и как она связана с силой роста?

14.В каких случаях целесообразно использовать непрерывное начисление процентов?