Номинальная и эффективная ставки процентов

Начисление сложных процентов

Сложные проценты

Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов.

Формула наращения по сложным процентам

Пусть первоначальная сумма долга равна P, тогда через один год сумма долга с присоединенными процентами составит P(1+i), через 2 года P(1+i)(1+i)=P(1+i)², через n лет - P(1+i)ⁿ. Таким образом, получаем формулу наращения для сложных процентов

S=P(1+i)ⁿ, (19)

где S- наращенная сумма,i - годовая ставка сложных процентов, n - срок ссуды, (1+i)ⁿ - множитель наращения.

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.). Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен P, а знаменатель (1+i).

Отметим, что при сроке n<1 наращение по простым процентам дает больший результат, чем по сложным, а при n>1 - наоборот. В этом нетрудно убедиться на конкретных числовых примерах. Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается в средней части периода.

Формула наращения по сложным процентам,
когда ставка меняется во времени

В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

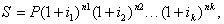(20)

где i₁, i₂,..., i_k - последовательные значения ставок процентов, действующих в периоды n1, n2,..., nk соответственно.

Пример 6.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа (обозначение разницы между процентными ставками и другими показателями.)10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.

Решение.

(1+0,3)²(1+0,28)(1+0,25)=2,704

Начисление годовых процентов при дробном числе лет

При дробном числе лет проценты начисляются разными способами:

1) По формуле сложных процентов

S=P(1+i)ⁿ, (26)

2) На основе смешанного метода, согласно которому за целое число лет начисляются сложные проценты, а за дробное - простые

S=P(1+i)^a(1+bi), (27)

где n=a+b, a-целое число лет, b-дробная часть года.

3) В ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т.е.

S=P(1+i)^a. (28)

Номинальная и эффективная ставки процентов

Номинальная ставка. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году m. Тогда каждый раз проценты начисляют по ставкеj/m. Ставка jназывается номинальной. Начисление процентов по номинальной ставке производится по формуле:

S=P(1+j/m)^N, (29)

где N - число периодов начисления.

Если срок ссуды измеряется дробным числом периодов начисления, то при m разовом начислении процентов в году наращенную сумму можно рассчитывать несколькими способами, приводящими к различным результатам:

1) По формуле сложных процентов

S=P(1+j/m)^N/t, (30)

где N/t - число (возможно дробное) периодов начисления процентов, t - период начисления процентов,

2) По смешанной формуле

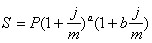, (31)

где a - целое число периодов начисления (т.е. a=[N/t] - целая часть от деления всего срока ссуды N на период начисления t),

b- оставшаяся дробная часть периода начисления (b=N/t-a).

Пример 8.

Размер ссуды 20 млн. руб. Предоставлена на 28 месяцев. Номинальная ставка равна 60% годовых. Начисление процентов ежеквартальное. Вычислить наращенную сумму в трех ситуациях: 1) когда на дробную часть начисляются сложные проценты

Решение.

Начисление процентов ежеквартальное. Всего имеется 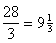кварталов.

1) 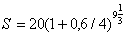= 73,713 млн. руб.

Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m -разовое наращение в год по ставке j/m.

Если проценты капитализируются m раз в год, каждый раз со ставкой j/m, то, по определению, можно записать равенство для соответствующих множителей наращения:

(1+i_э)ⁿ=(1+j/m)^mn, (32)

где i_э - эффективная ставка, а j - номинальная. Отсюда получаем, что связь между эффективной и номинальной ставками выражается соотношением

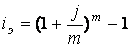(33)

Обратная зависимость имеет вид

j=m[(1+i_э)^1/m-1]. (34)

Пример 9.

Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки 10% годовых.

Решение

i_э=(1+0,1/4)⁴-1=0,1038, т.е. 10,38%.

Пример 10.Определить какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 12% годовых.

Решение.

j=4[(1+0,12)^1/4-1]=0,11495, т.е. 11,495%.