Пример 1.2.11. Из какого капитала можно получить 24 тыс. руб. через два года наращением по простым процентам по процентной ставке 25%? Чему равен дисконт?
Решение. Пользуясь формулой (18), где F = 24 тыс. руб., n = 2 года, r = 0,25, получим:
P=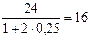 
тыс. руб.
Отсюда можно найти дисконт: Dr =F – P=24 – 16 = 8 тыс. руб. Этот дисконт представляет собой 50% (процентная ставка за два года) "на 100" с 24 тыс. руб. Действительно, по формуле (7):
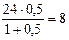
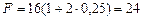тыс. руб.
С целью проверки можно по формуле (9) определить наращенную сумму с капитала Р = 16 тыс. руб. за 2 года по просто процентной ставке 25% годовых:
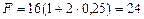тыс. руб.
Дисконтный множитель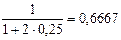 
представляет величину, обратную множителю наращения 1 + 2 • 0,25, и показывает долю капитала Р=16 тыс. руб. в капитале F = 24 тыс. руб.
Пример 1.2.12. Вам 27 декабря будет нужна сумма 15 тыс. руб. Какую сумму 10 июня этого же года Вы должны положит в банк под простую процентную ставку 36% годовых, если в расчете применяется обыкновенный процент с точным числом дней?
Решение. Полагая в формуле (18) F =15 тыс. руб., n = 200/360 года (200 дней), r = 0,36, получим:
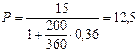тыс. руб.
Если бы в расчете применялся точный процент с точным числом дней, то величина вклада должна быть несколько большей. Так, для невисокосного года:
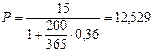тыс. руб.
что превышает полученную ранее сумму на 29 руб.
Пример 1.2.13. На какой срок клиент банка может взять кредит в размере 20 тыс. руб. под простые проценты с условием, чтобы величина возврата долга не превышала 22 тыс. руб., если процентная ставка равна 34%, в расчет принимаются точные проценты с точным числом дней и год високосный?
Решение. Полагая в формуле (21) для расчета срока в днях F=22 тыс. руб., Р = 20 тыс. руб., T = 366 дней, r =0,34, получим:
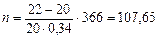дня.
Так что клиент банка может взять кредит не более чем на 107 дней. Для проверки по формуле (9) найдем наращенную сумму за 107 дней:
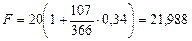тыс. руб.
Кстати, если взять 108 дней, то получим 22,007 тыс. руб., т.е. превышение всего на 7 руб., что, конечно, не является существенным.
Пример 1.2.14. Депозитный сертификат номиналом 20 тыс. руб. с начислением процентов по простой процентной ставке 40% годовых выпущен на один год. По какой цене его можно приобрести за 60 дней до срока погашения, чтобы обеспечить доходность такой финансовой сделки в виде простой процентной ставки 45% годовых? Расчетное количество дней в году равно 365.
Решение. Депозитный сертификат - документ, подтверждающий, что его владелец является держателем срочного депозита в банке. Для определения допустимой цены покупки сертификата необходимо его номинал вместе с начисленными за год процентами дисконтировать по простой процентной ставке 45% годовых, исходя из периода в 60 дней:
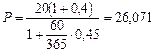тыс. руб.
Если бы в расчете применялся точный процент с точным числом дней, то величина вклада должна быть несколько бол шей. Так, для невисокосного года:
Если цена покупки депозитного сертификата будет больше полученной величины 26,071 тыс. руб., то при его приобретении доставляется доходность, меньшая 45%.
Простая учетная ставка
Основные положения
· Банковское (коммерческое) дисконтирование применяется в ситуации предварительного начисления простого процента, например при операции по учету векселя, заключающейся в покупке банком или другим финансовым учреждением векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю в конце срока. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. Проценты, удерживаемые банком в свою пользу, часто называют дисконтом.
· Если специальным образом не оговорены условия, вексель, как правило, учитывается по простой учетной ставке и при этом используются обыкновенные проценты.
· Банковское дисконтирование (в отличие от математического) нельзя осуществить во всех ситуациях (например, по достаточно большой учетной ставке и задолго до срока платежа).
· Математическое дисконтирование выгоднее для векселедержателя, а банковское дисконтирование - для банка.
· Удержание простых процентов в момент предоставления ссуды можно рассматривать как соглашение между кредитором и должником о том, что наращение будет осуществляться по простой учетной ставке. Аналогичное соображение можно высказать и относительно операции учета векселя.
· При применении наращения на основе простой учетной ставки величина начисляемых процентов с каждым годом увеличивается, в то время как при наращении капитала на основе простой процентной ставки капитал ежегодно увеличивается на одну и ту же величину. Простая учетная ставка обеспечивает более быстрый рост капитала,чем такая же по величине процентная ставка.
· Финансовый результат, полученный с помощью простой учетной ставки, можно получить и с помощью эквивалентной ей простой процентной ставки.
· Финансовое соглашение может не только предусматривать постоянную учетную ставку на весь период, но и устанавливать изменяющуюся во времени (переменную) ставку.