Точка в ортогональной системе двух плоскостей проекций.

При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. На рисунке 2 показана точка А и ее ортогональные проекции А1 и А 2.

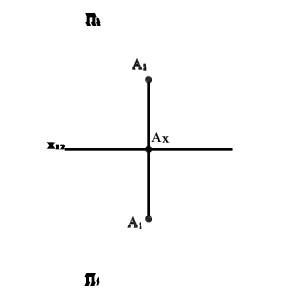
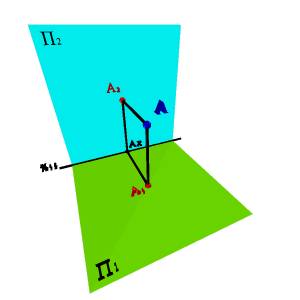
Рис. 2 Точка в системе двух плоскостей проекций

Точку А1 называют горизонтальной проекцией точки А, точка А2 - ее фронтальной проекцией. Проекции точки всегда расположены на прямых, перпендикулярных оси x12 и пересекающих эту ось в одной и той же точке А x.

На эпюре Монжа проекции А1 и А2 окажутся расположенными на одном перпендикуляре к оси x12. При этом расстояние А1Аx -от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П2, а расстояние А2Аx - от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П1.

Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.

ТОЧКА

Точка в ортогональной системе трех плоскостей проекций

В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью профильную плоскость проекций П3, расположенную перпендикулярно к П1 и П2.

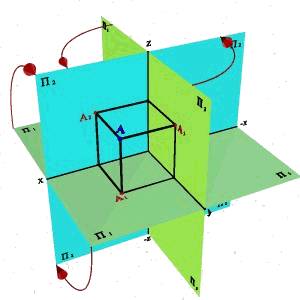
Рис. 3 Точка в системе трех плоскостей.

Модель трех плоскостей проекций показана на рис.3. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной.

Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3.

Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0.

Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте.

Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают, как показано на рисунке 3, до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают.

Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).

Октант	I	II	III	IV	V	VI	VII	VIII
x	+	+	+	+	-	-	-	-
y	+	-	-	+	+	-	-	+
z	+	+	-	-	+	+	-	-

Взаимное расположение точек

Можно выделить три основных варианта взаимного расположения точек:

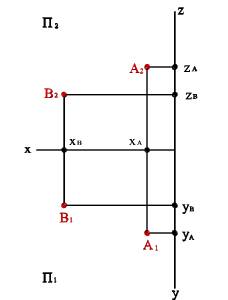
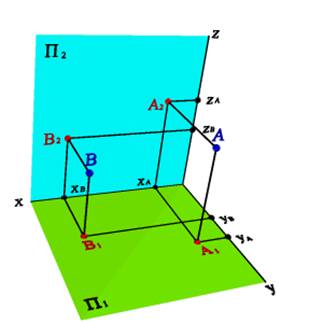
Рис. 4.Взаимное расположение точек

1.Пусть точки А и В (рис.4) расположены в первой четверти так, что:

- YА>YВ. Тогда точка А расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка В

- ZА>ZВ. Тогда точка А расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка В;

- XА<XВ. Тогда точка В расположена дальше от плоскости П3 и ближе к наблюдателю, чем (при взгляде слева) точка А;

2. – YА=YВ, то точки А и В равноудалены от плоскости П2 и их горизонтальные проекции расположатся на прямой А1В1//x12. Геометрическим местом таких точек служит плоскость, параллельная П2.

– ZА=ZВ, то точки А и В равноудалены от плоскости П1 и их фронтальные проекции расположатся на прямой А2В2//x12. Геометрическим местом таких точек служит плоскость, параллельная П1.

– XА=XВ, то точки А и В равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположатся, соответственно, на прямых А1В1//y и А2В2//z . Геометрическим местом таких точек служит плоскость, параллельная П3.

3. Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 5 даны три пары таких точек, у которых:

XА=XD;YА=YD;ZА>ZD; XA=XC;ZA=ZC;YA>YC; YA=YB;ZA=ZB;XA>XB;

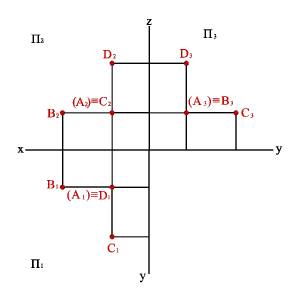
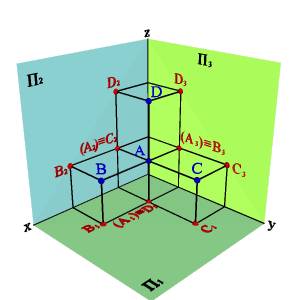
Рис. 5. Конкурирующие точки

Различают: горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD; фронтально конкурирующие точки A и C расположенные на фронтально проецирующей прямой AC; профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.

При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.

Прямая линия

Способы графического задания прямой линии

Для определения положения прямой в пространстве существуют следующие методы:

1.Двумя точками (А и В).

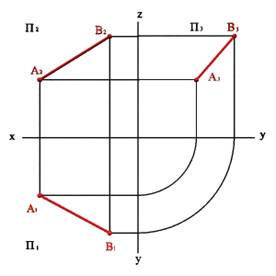
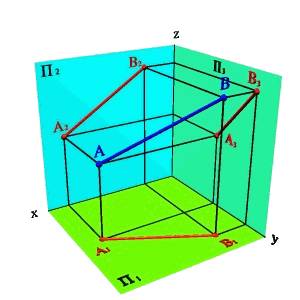
Рис. 6. Определение положения прямой по двум точкам

Рассмотрим две точки в пространстве А и В (рис.6). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].

2. Двумя плоскостями (a; b).

Этот способ задания определяется тем, что две непараллельные плоскости пересекаются в пространстве по прямой линии.

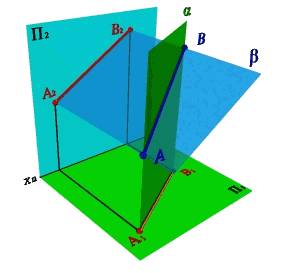
Рис. 7. Определение положения прямой в пространстве по двум проекциям отрезка

3. Двумя проекциями.

Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.7), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].

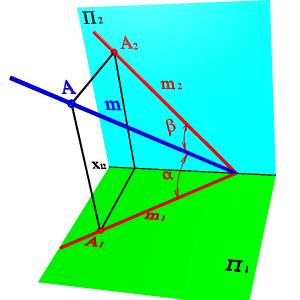
Рисунок 8. Определение положения прямой по точке и углам наклона к плоскостям проекций

4. Точкой и углами наклона к плоскостям проекций.

Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве (рис.8).