Средний геометрический индекс (У.С. Джевонс)
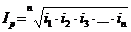(21.28),
где n – число индивидуальных индексов или число товаров.
Имеются данные об индексах цен на приобретаемые промышленными организациями основные виды топливно-энергетических ресурсов в 2007 г. (на конец квартала; в % к предыдущему кварталу):
| Вид топливно-энергетических ресурсов | 3 квартал | 4 квартал |
| А | 100,0 | 101,3 |
| Б | 84,8 | 100,4 |
| В | 101,0 | 106,7 |
| Г | 101,3 | 113,1 |
| Д | 103,4 | 102,2 |
| Е | 101,0 | 100,9 |
Источник: стат. сборник “Калужская область в 2007 году”
Определите среднее изменение цен с использованием индекса Карли и среднего геометрического индекса.
Решение: индекс Карли определяется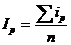 
.
Соответственно в 3 квартале он равен Iр =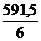 
= 98,6%. Цены сократились на 1,4%;
в 4 квартале Iр = 104,1%. Цены выросли на 4,1%.
Средний геометрический индекс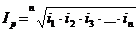 
.
В 3 квартале он равен Iр =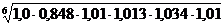 
= 0,984 или 98,4%. Цены сократились на 1,6%;
в 4 квартале Iр = 1,04 или 104,0%. Цены выросли на 4%.
Для характеристики изменения цен по разнородным видам товаров используют сводные (агрегатные) индексы:
1) индекс цен Э. Ласпейреса представляет собой сравнение агрегированных цен, взвешенных по физическим объемам базисного периода и вычисляется по формуле:
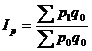(21.29),
где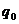 
- количество товара в базисном периоде;
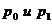- цена единицы товара соответственно в отчетном и базисном периодах.
Индекс показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию либо перерасход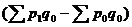 
, который можно было бы получить от изменения цен;
2) средний арифметический индекс цен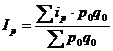 
(21.30);
3) индекс цен Г. Пааше представляет собой сравнение агрегированных цен, которые взвешены по физическим объемам текущего периода и определяется по формуле:
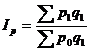(21.31).
Индекс показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или на сколько товары в отчетном периоде стали дороже либо дешевле, чем в базисном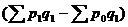 
;
4) средний гармонический индекс цен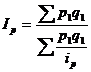 
(21.32);
5) “идеальный” индекс И. Фишера представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
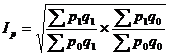(21.33);
6) индекс цен Эджворта- Маршалла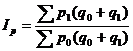 
(21.34).
Индекс показывает динамику цен в условиях среднего объема продаж отчетного и базисного периодов.
 |
Известны данные о средних ценах на отдельные виды группы товаров и объемах их покупки за два периода по одному из регионов РФ:
| Группы товаров | Средние потребительские цены, руб./кг | Объем покупки, кг/месяц | ||
| Базисный год | Отчетный год | Базисный год | Отчетный год | |
| Р0 | Р1 | q0 | q1 | |
| Хлебные продукты | 21,61 | 27,36 | 10,2 | 8,0 |
| Картофель | 9,55 | 10,69 | 6,0 | 5,8 |
| Рыба и рыбопродукты | 64,38 | 68,65 | 1,4 | 1,3 |
| Масло растительное | 37,50 | 58,89 | 1,0 | 0,8 |
Источник: стат. сборник “Калужская область в 2007 году”
Определите индексы цен Пааше, Ласпейреса, Фишера и Эджворта-Маршалла.
Решение: для облегчения расчетов построим разработочную таблицу
| Группы товаров | Р0q0 | Р1q1 | Р0(q0+ q1) | Р0q1 | Р1(q0+ q1) | Р1q0 |
| Хлебные продукты | 220,42 | 218,88 | 393,30 | 172,88 | 497,95 | 279,07 |
| Картофель | 57,3 | 62,00 | 112,69 | 55,39 | 126,14 | 64,14 |
| Рыба и рыбопродукты | 90,13 | 89,25 | 173,83 | 83,69 | 185,36 | 96,11 |
| Масло растительное | 37,5 | 47,11 | 67,50 | 30,00 | 106,00 | 58,89 |
| ИТОГО | 405,35 | 417,24 | 747,32 | 341,96 | 915,45 | 498,21 |
Индекс цен по методике Пааше =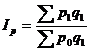 
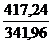= 1,220. Цены выросли на 22,0%.
Индекс цен по методике Ласпейреса =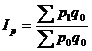 
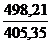= 1,229. Цены выросли на 22,9%.
“Идеальный индекс Фишера =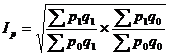 
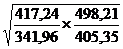= 1,224. Цены увеличились на 22,4%.
Индекс цен Эджворта- Маршалла =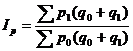 
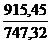=1,225. Цены выросли на 22,5%.
Для изучения изменения цен по однородным группам товаров по совокупности единиц исследования используют индексы средних уровней, которые характеризуютотносительное изменение средней цены. К индексам средних уровней относят:
- индекс переменного состава;
- индекс постоянного состава;
- индекс структурных сдвигов.
Индекс переменного состава характеризует увеличение или уменьшение средней цены по группе товаров в результате изменения цены каждого товара и структуры продукции:
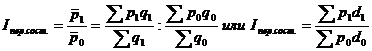(21.35 а,б),
где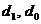 
- доля каждой группы товаров в общем объеме расходов в отчетном и базисном периодах,
определяется по формуле:
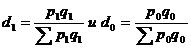(21.36 а,б).
Индекс постоянного состава характеризует изменение средней цены товара в результате влияния только одного фактора – изменения цен на отдельные товары:
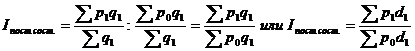(21.37 а,б).
Индекс структурных сдвигов характеризует влияние изменения структуры продукции на величину средней цены товара:
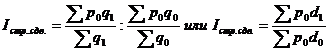(21.38 а,б).
Абсолютное изменение средней цены:
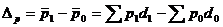(21.39),
за счет следующих факторов:
а) изменения цен на отдельные товары -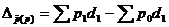 
(21.40),
б) изменения структуры продукции -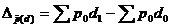 
(21.41).
 |
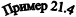Имеются данные о средних ценах на мясо и их объемах по трем регионам РФ за два периода:
| Регион | Средние цены, руб./кг | Объемы, тыс. т | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А | 143,82 | 149,71 | 5,3 | 4,9 |
| Б | 143,67 | 147,42 | 3,2 | 2,6 |
| В | 77,67 | 83,96 | 0,4 | 0,4 |
Источник: стат. сборник “Калужская область в 2007 году”
Определите относительное и абсолютное изменения средних цен.
Решение: относительное изменение средних цен характеризуется индексами переменного, постоянного составов и структурных сдвигов:
=
: 
=
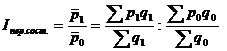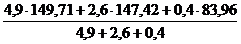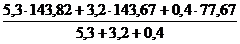=145,63/140,79 = 1,034;
= 
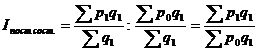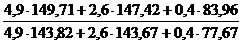= 145,63/140,42 =1,037;
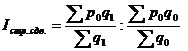= 140,42/140,79 = 0,997.
Проверка правильности расчетов 1,037 ·0,997 = 1,034.
Абсолютное изменение средней цены определяется
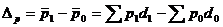= 145,63-14,79 = 4,84 руб.,
за счет следующих факторов:
а) изменения цен на отдельные товары - 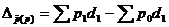= 145,63-140,42 = 5,21,
б) изменения структуры продукции - 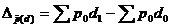= 140,42-140,79 = -0,37.
Правильность расчетов 5,21-0,37 = 4,84.
Средняя цена на мясо в отчетном периоде по сравнению с базисным увеличилась на 3,4% или 4,84 рубля. Это изменение было обусловлено ростом цен по каждому виду мяса на 3,7% или 5,21 рублей и уменьшением в структуре продукции дорогих видов мяса на 0,3% или 0,37 рублей.