Простые (арифметические) процентыпо вкладу
Пусть некий человек, назовём его экономическим агентом или вкладчиком, кладёт на счёт в банке V денежных единиц, например 1000 р.
По условиям договора банк обязуется ежегодно выплачивать вкладчикуфиксированную долю вклада. Чаще всего эта доля выражена в процентах иназывается процентом по депозиту (вкладу). Обозначим этот показа тельчерез r. Обозначение связано с английским термином interest rate.
В концепервого года хранения денег в банке вкладчик получит доход Vr/100
единиц.
Для того чтобы формулы были менее громоздкими, процент по вкладуудобнее выражать в долях. Например, в процентах — 5%, а в долях — 0,05.
Если выражать процент по вкладу в долях, то в конце года вкладчик полу-
чит Vr денежных единиц.
Если вкладчик забирает проценты, а вклад остаётся в банке, то в конце следующего года вкладчик получит ещё Vr денежных единиц. Другимисловами, за два года вкладчик получит 2Vr единиц. Аналогично за t летвкладчик получит Vrt денежных единиц.
Вкладчик может не забирать накопившиеся к концу года проценты, адобавлять эту сумму к основному вкладу. Договор с простыми процентамихарактеризуется тем, что проценты на проценты неначисляются. Условиядоговора по начислению процентов распространяются только на основной вклад.
В этом случае к концу года t вклад будет составлятьVt = V(1 + rt)денежных единиц.
Для целочисленного положительного (натурального) tвеличина вклада представляет собой арифметическую прогрессию с разностью Vr. Индекс t подчёркивает, что мы рассматриваем величину вкладакак функцию времени (числа лет), а первоначальный размер вклада V иставка процента r рассматриваются как параметры.
Формула ясно указывает, что при начислении простого процента размер вклада
растёт как линейная функция времени.
Заметим, что величина накопленного вклада будет такой же в концепериода, если процент по вкладу уменьшить в 2 раза, но подождать вдвоебольше времени.
Геометрическое место точек плоскости (r, t) таких, чтозначение функции Vtсохраняется постоянным, называется линией уровняэтой функции (рис. 1). Уравнение этой линии для вклада с простым начислением процентов имеет вид: V(1 + rt) = const.
При заданном начальномвкладе эта линия — ветвь гиперболы rt = k, лежащая в первом квадранте(по горизонтальной оси отложено время, по вертикальной — доля). При
построении графика время рассматривается как непрерывное, хотя доходвыплачивается только в конце каждого года.
Если вкладчик планирует держать деньги в банке несколько лет, то начисление простых процентов явно невыгодно для него. Вкладчик быстросообразит, что ему выгоднее забрать вклад и проценты в конце года и тутже вложить увеличенную за счёт процентов сумму денег ещё на один год,через год повторить эту операцию, и так каждый год. При такой стратегииежегодные проценты будут начисляться на всю накопленную сумму, а нетолько на первоначальный вклад.
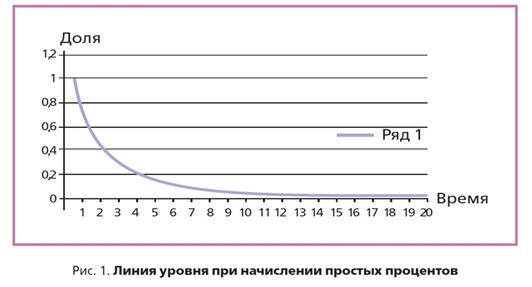
(5, с. 8-10)
Сложные проценты по вкладу
Для того чтобы избежать бессмысленных операций ежегодного закрытия вклада и открытия его вновь, банк предлагает клиентам схему начисления сложных процентов.
Начисление сложных процентов эквивалентно тому, что срок размещения вклада всегда составляет только один год, нопервоначальная сумма ежегодно растёт за счёт начисленных в предыдущем году процентов. После первого года вклад составит, как и при простыхпроцентах, V1 = V(1 + r). После второго года — V2 = V(1 + r)2. Аналогично к
концу года t вклад будет составлять Vt = V(1 + r)t.
При начислении сложных процентов величина вклада увеличиваетсяпо формуле геометрической прогрессии с показателем (1 + r). Теперь величина вклада растёт не как линейная, а как показательная функция.
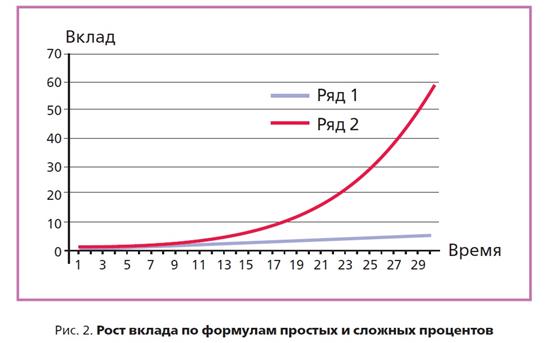
На рис. 2показано, как растёт вклад при начислении дохода по формуле простых исложных процентов. По горизонтальной оси отложено время, а по вертикальной — размер вклада. Начальный вклад полагается равным одной денежной единице. Обратите внимание, что при малом сроке хранениявклада величина депозита незначительно различается для двух разных способов начисления процентов. При сроке хранения вклада в несколькодесятков лет разница становится очень большой.
Линия уровня стоимости вклада при начислении сложного процента имеет вид:
t・ln(1 + r) = const (по горизонтальной оси отложено время, по вертикальной — доля) (рис. 3).
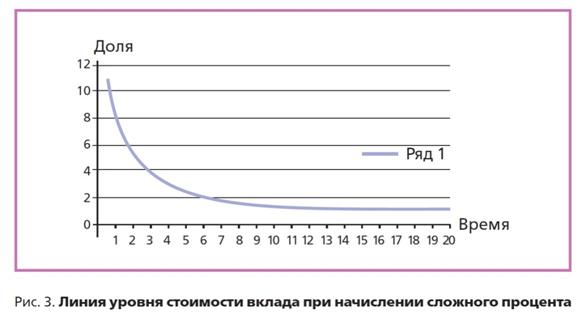
Применим выведенные формулы для решения следующей задачи.
Задача
Папа первоклассницы Тани решил накопить денег на выпускной вечер дочери. Он положил 1000 р. на счёт в банке под годовой номинальный процент 10%. Найдите сумму, которая накопится на вкладе к окончанию Таней средней школы, если проценты начисляются ежегодно:
а) по формуле простых процентов;
б) по схеме сложных процентов.
Решение.
Применение формулы простых процентов даёт 1000 ・ (1 + + 0,1 ・ 11) р. через 11 лет.
В итоге в пункте а) папа накопит к Таниному выпускному вечеру 2200 р.
При ежегодном начислении сложных процентов к выпускному вечеру будет накоплено 1000 ・ (1 + 0,1)11 = 2853 р. 12 к.
Накопленная сумма будет примерно в 1,4 раза больше, чем при начислении простых процентов.
(5, с. 10 -12)
Сложно-простые проценты
Существует ещё одна схема начисления процентов на вклад, иногда называемая сложно-простыми процентами. При этой схеме устанавливается годовая ставка процента r, но начисление процентов проводится несколько раз в год. Например, начисление может проводиться ежеквартально или ежемесячно.
Обозначим количество раз начисления процентов в течение года через натуральное число m. Тогда в конце первого периода начисления вклад увеличивается до величины
V(1 + r/m).
Другими словами, при увеличении вклада в конце каждого периода используется формула простого процента.
Но в следующий период процент начисляется уже с учётом увеличения вклада, т. е. «работает» формула сложного процента.
Поэтому к концу года вклад станет равен величине V(1 + r/m)m.
К концу года t вклад будет составлять величину
Vt= V(1 +r/m)mt.
Параметр m входит в эту формулу дважды. При его увеличении уменьшается выражение, заключённое в скобки, но увеличивается показатель степени, в которую выражение в скобках возводится. Можно доказать (см. упражнения), что при постоянных величинах r и t выражение Vt= V(1 + r/m)mt монотонно растёт при увеличении m. При одном и том же годовом проценте чем чаще происходит начисление, тем больше величина вклада к концу года.
Рассмотрим не очень жизненный, но математически легко понимаемый пример. Пусть вкладчик кладёт в банк 1 р., но под 100% годовых. Рассчитаем размер вклада через один год. В зависимости от переменной m размер вклада составит величину, представленную в таблице 1.
В первом столбце указано количество начислений в течение года. Первая строка соответствует ежегодному начислению процента, 12-я — ежемесячному начислению, 52-я — еженедельному.
Второй столбец показывает величину вклада в конце года, а третий — процент, при котором однократное начисление могло бы дать такую же величину вклада. Этот показатель принято называть эффективным процентом, а годовой процент r — номинальным процентом.
Мы видим, что при еженедельном начислении (m = 52) номинальному проценту 100% соответствует эффективный процент более 169%. При ежедневном начислении (m = 365) эффективный процент достигает почти 171,5%. Дальнейшее увеличение числа m
практически не меняет эффективный процент.
Таблица 1. Величина вклада в конце года и эффективный процент
при разном количественачислений процента в течение года
| Количествоначисленийвгоду(m) | Величинавкладавконцегода | Эффективныйпроцент |
| 2,25 | ||
| 2,37037037 | 137,037037 | |
| 2,44140625 | 144,140625 | |
| 2,48832 | 148,832 | |
| 2,521626372 | 152,1626372 | |
| 2,546499697 | 154,6499697 | |
| 2,565784514 | 156,5784514 | |
| 2,581174792 | 158,1174792 |
Продолжение
| Количествоначисленийвгоду(m) | Величинавкладавконцегода | Эффективныйпроцент |
| 2,59374246 | 159,374246 | |
| 2,604199012 | 160,4199012 | |
| 2,61303529 | 161,303529 | |
| … | … | … |
| 2,692596954 | 169,2596954 | |
| … | … | … |
| 2,714567482 | 171,4567482 | |
| … | … | … |
| 2,716923932 | 171,6923932 | |
| … | … | … |
| 2,718280469 | 171,8280469 | |
| 2,718282053 | 171,8282053 |
Из таблицы видно, что при увеличении количества начислений величина вклада в конце года действительно монотонно растёт. Можнодоказать этот вывод строго математически, используя разложение степени по формуле бинома Ньютона.
Но растёт вклад не безгранично,при больших значениях параметра m его дальнейшее увеличениепочти не меняет величину вклада в конце года. На языке математикиэто означает, что существует предел выражения Vm= V(1 + 1/m)m, который
соответствует бесконечно частому начислению процента.
Конечно,на практике такое невозможно, бесконечно частое начисление процента существует только абстрактно. Такой контракт с банком называется мгновенно начисляемым сложным процентом. Используя математическое определение предела, можно утверждать, что существует
limn→ ¥(1 + 1/n)n,
и этот предел и есть величина вклада в 1 р. в конце годахранения при мгновенном начислении сложных процентов и годовомноминальном проценте 100%.
(5, с. 13 – 15)
Экономический смысл числае
Величина рассмотренного выше предела обозначается знакомымвам иррациональным числом, являющимся основанием натуральных логарифмов, — числом e. Его примерная величина равна 2,7182.
Напомним,что это иррациональное число не может быть выражено ни в виде простойдроби, ни в виде бесконечной периодической десятичной дроби. Итак,
limn→ ¥(1 + 1/n)n = e.
Мы получили следующее экономическое содержание числа e.
Основание натуральных логарифмов соответствует величине вклада в 1 р. после одного года хранения при мгновенном начислении сложных процентов и годовом номинальном проценте 100%. В конце года tнакопленный размер вклада составит
limn→¥(1 + 1/n)nt = (limn→¥(1 + 1/n)n)t= et.
(5, с. 16)
ИСТОЧНИКИ
1. Абросимова Е. А. Финансовая грамотность: материалы для воспитанников детских домов и учащихся школ-интернатов / Е. А. Абросимова. — М.: ВИТА-ПРЕСС, 2015. — 192 с.
2. Абросимова Е. А. Финансовая грамотность: материалы для учащихся. 10–11 классы общеобразоват. орг., юридический профиль / Е. А. Абросимова. — М.: ВИТА-ПРЕСС, 2015. — 160 с.
3. Брехова Ю. В. Финансовая грамотность: материалы для учащихся. 10–11 классы общеобразоват. орг. / Ю. В. Брехова, А. П. Алмосов, Д. Ю. Завьялов. — М.: ВИТА-ПРЕСС, 2015. — 400 с.
4. Жданова А. О. Финансовая грамотность: материалы для обучающихся. СПО / А. О. Жданова. — М.: ВИТА-ПРЕСС, 2015. — 400 с.
5. Канторович, Г. Г. Финансовая грамотность: материалы для учащихся. 10–11 классы общеобразоват. орг. Математический профиль / Г. Г. Канторович. — М.: ВИТА-ПРЕСС, 2015. — 96 с.
6. Киреев А. П. Финансовая грамотность: материалы для учащихся. 10–11 классы общеобразоват. орг., экономический профиль / А. П. Киреев. — М.: ВИТА-ПРЕСС, 2015. — 368 с.
7. Липсиц И. В. Финансовая грамотность: материалы для учащихся. 8–9 классы общеобразоват. орг. / И. В. Липсиц, О. И. Рязанова. — М.: ВИТА-ПРЕСС, 2015. — 352 с.
8. Савицкая Е. В. Финансовая грамотность: материалы для обучающихся по основным программам профессионального обучения / Е. В. Савицкая. — М.: ВИТА-ПРЕСС, 2015. — 224 с.
9. Гусева А.А.. Рынок ценных бумаг. — 2006. Электронный источник: http://www.be5.biz/rynok_tcennykh_bumag/investicionnye_operacii.html
Дата: 09.03.2017.
10. Энциклопедия Кольера. Инвестирование. — Открытое общество. 2000. Электронный источник: http://dic.academic.ru/dic.nsf/enc_colier/452/%D0%98%D0%9D%D0%92%D0%95%D0%A1%D0%A2%D0%98%D0%A0%D0%9E%D0%92%D0%90%D0%9D%D0%98%D0%95
Дата: 09.03.2017.
[1]Цифры в таблице примерные, для более точной информации следует
получить сведения в кредитной организации.
[2] Стартап (от англ. startup — запуск) — недавно созданная компания.
