Рекуррентная формула для числа сочетаний без повторений. Треугольник Паскаля.

Вычислять числа сочетаний без повторений можно не только по прямой формуле 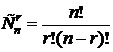, но и по рекуррентной формуле, где каждое новое значение числа сочетаний вычисляется на основе предыдущих значений. Выведем эту формулу.

Зафиксируем в n‑множестве некоторый элемент и рассмотрим r‑сочетания без повторений из этого n‑множества. Относительно любого сочетания можно сказать, содержит ли оно данный зафиксированный элемент или нет.

Если содержит, то остальные (r-1) элементов сочетания выбираются из (n-1)-множества. Число способов выбрать (r-1) элемент из (n-1)-множества без учета порядка: .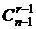

Если не содержит (в сочетании этого элемента нет), то это r‑сочетания из (n-1)-множества (то есть из множества, в котором удален данный элемент). Число способов выбрать r элементов из (n-1)-множества без учета порядка: .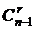

Эти два случая взаимоисключающие, поэтому по правилу суммы

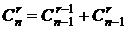
с начальными условиями

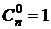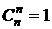, и при r>n .

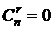Таким образом, числа сочетаний без повторений (биномиальные коэффициенты) можно вычислять не только по прямой формуле, но и рекуррентно. Построим таблицу для биномиальных коэффициентов. Исходя из начальных условий, в столбце 0 и на диагонали находятся единицы, а все клетки, находящиеся выше диагонали, содержат нули. Из рекуррентной формулы следует, что для получения значения в n-й строке r-м столбце (заданная клетка) нужно сложить значение в (n-1)‑й строке r-м столбце (клетка сверху над заданной) и значение в (n‑1)‑й строке (r-1)-м столбце (клетка сверху слева от заданной).

r n

…

Бином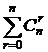

(a+b)0 = 1

1=20

(a+b)1 = 1a+1b

2=21

(a+b)2 = 1a2+2ab+1b2

4=22

(a+b)3 = 1a3+3a2b+3ab2+1b3

8=23

(a+b)4 = 1a4+4a3b+6a2b2+4ab3+1b4

16=24

M

32=25

64=26

128=27

256=28

M

M

M

M

M

M

M

M

M

M

M

Эта таблица называется треугольником Паскаля. Он позволяет быстро находить числа сочетаний без повторений и не требует вычисления факториалов.

Видно, что в каждой строке таблицы сумма чисел равна степени двойки. Это свойство чисел сочетаний без повторений, которое будет доказано ниже.

Некоторые комбинаторные соотношения для чисел сочетаний без повторений

(1).

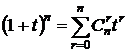
# Следует из того, что 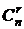– коэффициенты бинома:

.

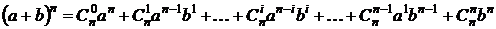Подставляя вместо a единицу, вместо b – t, получим формулу (1). #

(2). 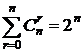. # получается из (1) при t =1. #

(3). 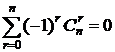. # следует из (1) при t = -1. #

(4).

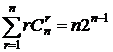
# продифференцируем (1) по t: ,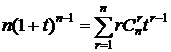

затем подставим t =1: #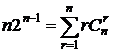

(5).

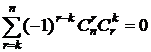
# продифференцируем (1) по t k раз:

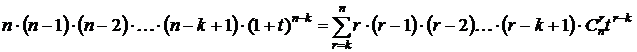подставляем t = -1:

,

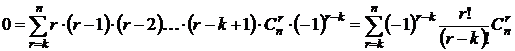разделим левую и правую часть на k!

#

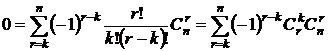(6).

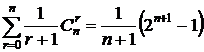
# проинтегрируем левую и правую часть (1) от 0 до 1:

,

. #

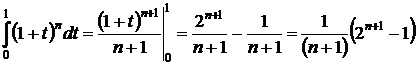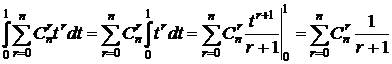(7). 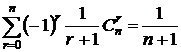. # интегрируем (1) от -1 до 0. #

(8). 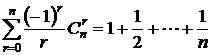- гармонический ряд

(9).

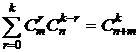
(10). Если p – простое число, то каждое из чисел 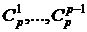делится на p.

# , , , … , . #

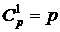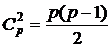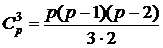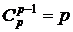Лекция 3.