Некоторые сведения из теории множеств
КОМБИНАТОРИКА
Некоторые сведения из теории множеств
Множество – любое собрание объектов, определённых и хорошо различимых нашей интуицией или интеллектом, мыслимое как единое целое (Георг Кантор, 1872 г.).
Множества обозначаются большими буквами, элементы множества – малыми.
Принадлежность. Если x принадлежит множеству S (x является элементом S), то это обозначается xÎS. Если x не принадлежит S – xÏS.
Пример: S={a,b,c}, aÎS, bÎS, cÎS, dÏS.
Подмножество. Отношение включения.Если все элементы множества А принадлежат множеству B, то А – подмножество множества B. Это обозначается так: АÍB (А не строго включается в B). Если при этом в B есть элементы, не принадлежащие А, то это обозначают АÌB (А строго включается в B; A – собственное подмножество B).
Универсальное множество – множество всех элементов какого-либо определённого типа.
Пустое множество (Æ) – множество, не содержащее ни одного элемента. По определению, пустое множество является подмножеством любого множества. (" S : ÆÍS).
Мощность множества. Для конечных множеств мощность –количество элементов во множестве. Мощность множества S обозначается |S|. Например, S={a, b, c}, |S|=3.
Множества называются равномощными (эквивалентными), если их мощность равны.
Операции над множествами
Пусть заданы множества A и B.
Объединениемножеств A и B – множество АÈВ={x : xÎA или xÎB} (объединение содержит элементы, которые есть или в A, или в B, или в том и другом множестве). (нарисовать с помощью кругов Эйлера). АÈВ= BÈA.
Пересечениемножеств A и B – множество АÇВ={x : xÎA и xÎB} (пересечение содержит элементы, которые есть одновременно и в A, и в B. (нарисовать). АÇВ= BÇA.
Дополнение до универсальногомножества. Если В – универсальное множество, и АÍВ, то дополнение 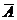 ={x : xÎB и xÏA}. (нарисовать).
={x : xÎB и xÏA}. (нарисовать).
Произведениемножеств A и B – множество AxB={<x, y> : xÎA, yÎB} (множество всех пар, первый элемент которых принадлежит множеству A, второй элемент – множеству B). Мощность произведения AxB равна произведению мощностей A и B (|AxB|=|A|*|B|). Произведение BxA не равно AxB, но их мощности совпадают (BxA ¹ AxB, но |BxA| = |AxB|).
Пример: A={a, b, c}, B={c, d}, |A|=3, |B|=2.
АÈВ={a, b, c, d}, АÇВ={c}, AxB={<a,c>, <a,d>, <b,c>, <b,d>, <c,c>, <c,d>}, BxA={<c,a>, <c,b>, <c,c>, <d,a>, <d,b>, <d,c>}, |AxB|=6, |BxA|=6.
Оператор (функция) – правило, определяющее отображение некоторого множества X в некоторое множество Y. Обозначение: F : X®Y.
Пример: X={a, b, c, d}, Y={▲, ●, ■}. Возможный вариант функции: f(a)=■, f(b)=●, f(c)=■, f(d)=▲.
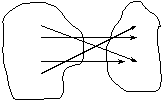 X Y a ▲ b ● c ■ d X Y a ▲ b ● c ■ d |
Дискретное множество – множество, состоящее из изолированных точек (т.е. множество, не имеющее предельных точек). Например, множество натуральных чисел – дискретное множество, а множество действительных чисел – непрерывное множество.
Дискретная математика изучает свойства дискретных множеств и определённых на них операторов. Непрерывными множествами занимается математический анализ.
Лекция 1.
Проблемы и задачи комбинаторики
Комбинаторика изучает приёмы нахождения числа различных комбинаций, составленных из данных предметов (элементов дискретного множества предметов) при определённых условиях.
Комбинация – некоторое сочетание предметов.
Типы комбинаторных проблем
1. Проблемы существования. Доказывается теоретически, что есть решение или нет.
2. Если решения задачи есть, то сколько их.
3. Выбрать наиболее экономичный способ решения.
Типы комбинаторных задач
1. Задача о маршрутах.
2. Задача о размещении.
3. Задача о покрытии.
4. Задача об укладке.
5. Задача о разбиении.
Все остальные задачи представляют собой объединение, пересечение, произведение указанных типов задач.
Пусть S – множество из n элементов (|S|=n). Говорят, что S – n-множество.
    T1 T2 Tn T1 T2 Tn |
Задача о покрытии
Найти такие множества Ti, i = 1, 2, …, r, чтобы 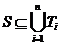 (чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков пола быть не должно.
(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков пола быть не должно.
Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда число множеств Ti должно быть минимальным, сами они должны содержать минимально возможное число элементов.
Задача о укладке
Найти такие попарно непересекающиеся множества Ti, i = 1, 2, …, r, (Ti ÇTj = Æ при i¹j) чтобы 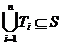 (чтобы объединение этих множеств вошло в S). (нарисовать)
(чтобы объединение этих множеств вошло в S). (нарисовать)
Например, уложить несколько предметов в одну коробку. Между предметами могут быть пустые промежутки, но сами предметы друг с другом не пересекаются и укладываются в коробку.
Во многих задачах укладка должна быть наиболее экономичной, когда укладывается максимально возможное количество предметов, а количество пустых промежутков должно быть как можно меньше.
Задача о разбиении
Найти такие попарно непересекающиеся множества Ti, i = 1, 2, …, r, (Ti ÇTj = Æ при i¹j) чтобы 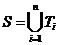 (чтобы объединение этих непересекающихся множеств дало S). (нарисовать)
(чтобы объединение этих непересекающихся множеств дало S). (нарисовать)
Например, группы в институте – это разбиение множества студентов института. Группы не пересекаются, а их объединение дает множество всех студентов института.
Правило суммы
Если объект a можно выбрать p способами, а объект b – другими q способами, то выбор “либо a, либо b” может быть осуществлен p+q способами. При этом выборы a и b являются взаимно исключающими.
Например, в вазе лежит 3 яблока и 5 груш. Тогда взять из вазы либо одно яблоко, либо одну грушу (взаимоисключающие события) можно 3+5 = 8 способами.
Обобщённое правило суммы
Пусть дано r множеств Ti (i=1,…,r), каждое из которых содержит ni элементов (Ti - ni‑множество), причём множества взаимно не пересекаются: TiÇTj=Æ при i¹j. Тогда объединение этих множеств S=T1È T2È…ÈTr есть (n1+…+nr)-множество. 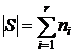 .
.
Правило произведения
Если объект a можно выбрать p способами, и после каждого из таких выборов объект b можно выбрать q способами, то выбор “a и b” в указанном порядке может быть осуществлен p·q способами. При этом выборы a и b являются независимыми.
Например, в вазе лежит 3 яблока и 5 груш. Тогда взять из вазы одно яблоко и одну грушу (события происходят совместно) можно 3·5 = 15 способами.
Лекция 2.
Виды выборок
Комбинаторику интересуют результаты отбора (построения выборок) и упорядочения элементов, выраженные в комбинаторных числах. Если после выбора элемент из множества удаляется (его нельзя еще раз выбрать) – это выборка без повторений. Если после выбора элемент из множества не удаляется и его можно выбрать еще раз – это выборка с повторениями. Если в выборках важен порядок элементов – это перестановки. Если же выборки с разным порядком элементов считаются одинаковыми – это сочетания.
С понятием отбора элементов в комбинаторике связано понятие выборки. Выборки могут быть упорядоченными и неупорядоченными, без повторений элементов и с повторениями.
Обозначим знаком 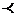 отношение упорядоченности. Тогда запись
отношение упорядоченности. Тогда запись 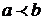 означает, что a предшествует b, а
означает, что a предшествует b, а 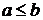 - a предшествует или совпадает с b.
- a предшествует или совпадает с b.
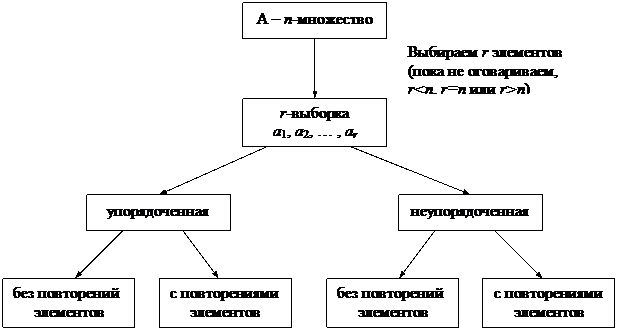
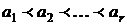 | 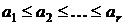 | ||
r-перестановка без повторений из n-множества 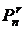 | r-перестановка c повторениями из n-множества 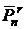 | r-сочетание без повторений из n-множества 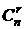 | r-сочетание с повторениями из n-множества 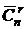 |
Число перестановок обозначается буквой P (permutation), число сочетаний – буквой C (conjunction). Произносится:
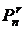 - “P из n по r” или “P по r из n”;
- “P из n по r” или “P по r из n”;
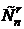 - “C из n по r” или “C по r из n”.
- “C из n по r” или “C по r из n”.
Все числа, существующие в комбинаторике, так или иначе, являются комбинациями этих четырех чисел.
Лекция 3.
Следствие 1.
Так как 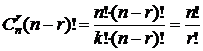 ,
,
то 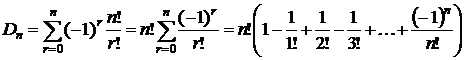 .
.
Следствие 2.
Так как 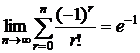 , то
, то 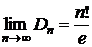 .
.
Следствие 3.
Рекуррентная формула для числа беспорядков: 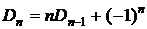 .
.
# 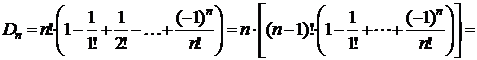
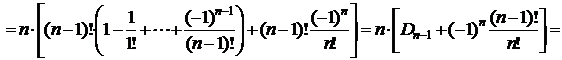
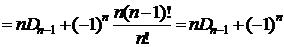 #
#
Следствие 4. 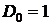
# По рекуррентной формуле из следствия 3 получаем 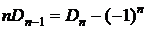 или
или 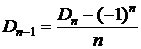 . При n=1 получаем
. При n=1 получаем 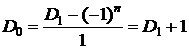 . По формуле из следствия 1 получаем
. По формуле из следствия 1 получаем 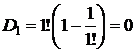 . Следовательно,
. Следовательно, 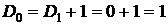 . #
. #
Следствие 5.
Ещё одна рекуррентная формула для числа беспорядков: 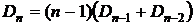 .
.
# Рассмотрим n элементов x1, x2, … , xn. Переставим их так, чтобы получить беспорядок. Начнём с x1: возьмём x1 и подставим его на место i-го элемента (i¹1). Тогда xi можно поставить на либо на первое место, либо на какое-то другое, кроме i-го. Если x1 стоит на i-м месте, а xi – на 1-ом, то число таких беспорядков – Dn-2 (т.е. число беспорядков оставшихся n-2 элементов). Если x1 не стоит на первом месте, то такой беспорядок определяется условием:
x2 не стоит на 2-м месте,
x3 не стоит на 3-м месте,
…
xi-1 не стоит на (i-1)-м месте,
xi не стоит на 1-м месте,
xi+1 не стоит на (i+1)-м месте,
…
xn не стоит на n-м месте.
Всего здесь n-1 элемент, то есть число таких беспорядков – Dn-1.
Итак, если x1 стоит на i-ом месте, то число таких беспорядков Dn-1+Dn-2. Но x1 можно поставить на любое из (n-1) мест (кроме 1-го). Для каждой установки x1 справедливы приведённые выше рассуждения.
Таким образом, общее число беспорядков – (n-1)(Dn-1+Dn-2). #
Для проверки полученной формулы вычислим количество беспорядков для некоторых значений n по рекуррентной и прямой формулам. По следствию 4, D0=1, D1=0.
| Рекуррентная формула | Нерекуррентная формула |
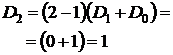 | 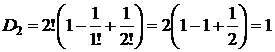 |
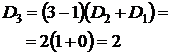 | 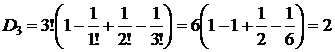 |
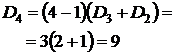 | 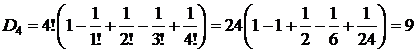 |
Для строгого доказательства правильности рекуррентной формулы, проверим ее в общем виде.
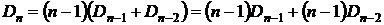 .
.
Из следствия 3 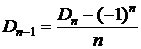 , следовательно,
, следовательно, 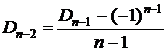 . Тогда
. Тогда
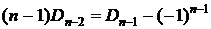 . Подставим этот результат в рекуррентную формулу:
. Подставим этот результат в рекуррентную формулу:
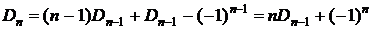 . Получили формулу из следствия 3.
. Получили формулу из следствия 3.
Обозначим через Dn,r число перестановок, в которых на своих местах остаются r элементов, а остальные (n-r) образуют беспорядок. Ясно, что Dn,n=1 (все элементы на своих местах), и Dn,0=Dn (ни одного элемента нет на своём месте).
Теорема. 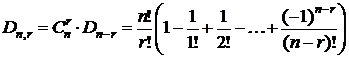 .
.
# r элементов, стоящих на своём месте, можно выбрать из n элементов 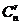 способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых Dn-r. Следовательно, всего таких перестановок
способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых Dn-r. Следовательно, всего таких перестановок 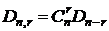 .
.
С другой стороны, (n-r) элементов, образующих беспорядки, можно выбрать 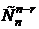 способами. Следовательно,
способами. Следовательно, 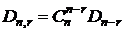 . В силу симметричности биномиальных коэффициентов
. В силу симметричности биномиальных коэффициентов 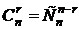 , обе формулы дают один и тот же результат.
, обе формулы дают один и тот же результат.
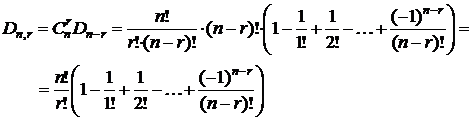 #
#
Пример.Выстраиваем 5 человек в определённом порядке, после чего 3 из них переставляем так, чтобы они не стояли на своих местах. Сколько таких перестановок?
Ответ: если трое не стоят на своих местах, то оставшиеся двое стоят на своих местах, т.е.
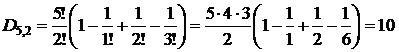 .
.
Следствие. 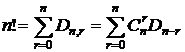 .
.
# Из n элементов можно образовать n! перестановок без повторений.
Среди них будет Dn,0 таких, где ни один элемент не стоит на своём месте;
Dn,1 таких, где по одному элементу стоит на своём месте;
Dn,2 таких, где по паре элементов стоит на своих местах;
и т.д.;
Dn,n=1 таких, где все элементы стоят на своих местах.
Следовательно, общее число перестановок (n!) равно сумме этих чисел. #
Теорема Лежандра
Введем обозначения:
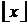 - наибольшее целое число, не превосходящее x (то есть для положительных x – целая часть x);
- наибольшее целое число, не превосходящее x (то есть для положительных x – целая часть x);
(a, b) – наибольший общий делитель (НОД) двух целых чисел a и b (a¹0, b¹0). Если (a, b)=1, то a и b взаимно простые (например, 4 и 9 – взаимно простые числа, так как их наибольший общий делитель - единица);
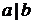 - а делит нацело b;
- а делит нацело b;
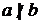 - а не делит нацело b.
- а не делит нацело b.
Теорема
Пусть дано N натуральных чисел a1, a2, … , aN, причем все эти числа попарно взаимно простые (то есть (ai, aj)=1 при i¹j). Тогда количество m натуральных чисел, не превышающих некоторого n (0<m£n) и взаимно простых с любым из a1, a2, … , aN (то есть 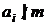 ,
, 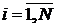 ) равно
) равно
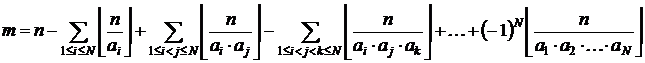
# Пусть S – n-множество натуральных чисел {1, 2, … , n}. Обозначим через pi свойство элемента множества S делиться нацело на ai ( 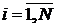 ).
).
Выражение 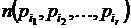 в формуле решета – это количество таких чисел, не превышающих n и делящихся нацело на каждое из чисел
в формуле решета – это количество таких чисел, не превышающих n и делящихся нацело на каждое из чисел 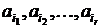 . По условию теоремы все ai попарно взаимно простые, следовательно,
. По условию теоремы все ai попарно взаимно простые, следовательно,
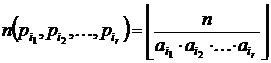 .
.
Подставляя эти числа в формулу решета, получим доказываемую формулу. #
Пример.Определим, сколько чисел, не превышающих 100, не делятся нацело на 4, 9 и 11. Всего чисел n=100. Среди них делящихся на 4 – 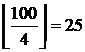 ; делящихся на 9 –
; делящихся на 9 – 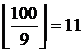 ; делящихся на 11 –
; делящихся на 11 – 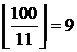 ; делящихся на 4 и 9 –
; делящихся на 4 и 9 – 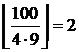 ; делящихся на 4 и 11 –
; делящихся на 4 и 11 – 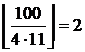 ; делящихся на 9 и 11 –
; делящихся на 9 и 11 – 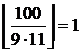 ; делящихся на 4, 9 и 11 –
; делящихся на 4, 9 и 11 – 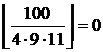 . Тогда по теореме Лежандра количество чисел, не превышающих 100 и не делящихся нацело на 4, 9 и 11, равно
. Тогда по теореме Лежандра количество чисел, не превышающих 100 и не делящихся нацело на 4, 9 и 11, равно
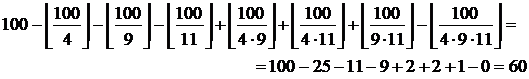
Функция Эйлера
Функция Эйлера φ(n), где n – натуральное число, дает количество натуральных чисел, не превышающих n и взаимно простых с n. Иначе говоря, φ(n)=k, где 0<k£n; (k,n)=1.
Теорема
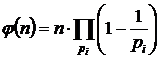 , где pi – все простые делители n. (
, где pi – все простые делители n. ( 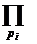 - произведение по всем простым делителям числа n).
- произведение по всем простым делителям числа n).
# В теореме Лежандра заменим ai на pi, где pi – простые делители n.
Тогда 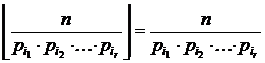 (так как pi делят n нацело).
(так как pi делят n нацело).
По теореме Лежандра
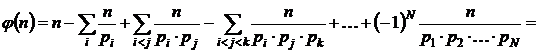
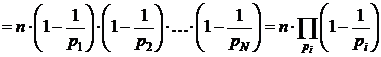 . #
. #
Пример.Определим, сколько чисел, не превышающих 100, взаимно простые с 100. Разложим число 100 на простые сомножители: 100=2·2·5·5=2252. Таким образом, у числа 100 два простых делителя – 2 и 5. По формуле Эйлера получаем
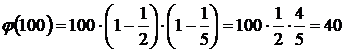 .
.
Таким образом, среди первой сотни есть 40 чисел, взаимно простых с 100.
Функция Мебиуса
Функция Мебиуса m(n), где n – натуральное число, принимает следующие значения:
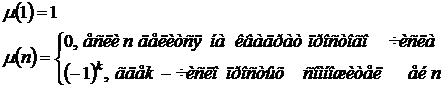
Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:
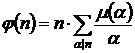 .
.
Суммирование идет по всем делителям n (а не только по простым делителям).
Пример. Вычислим φ(100), используя функцию Мебиуса.
Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}.
m(1) = 1,
m(2) = (-1)1 = -1 (у двойки один простой делитель – 2)
m(4) = 0 (4 делится на квадрат двойки)
m(5) = (-1)1 = -1 (у 5 один простой делитель – 5)
m(10) = (-1)2 = 1 (у 10 два простых делителя – 2 и 5)
m(20) = 0 (20 делится на квадрат двойки)
m(25) = 0 (25 делится на квадрат пятерки)
m(50) = 0 (50 делится и на 22, и на 55)
m(100) = 0 (100 делится и на 22, и на 55)
Таким образом,
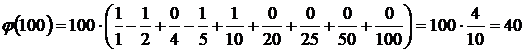
Свойство функции Мебиуса: 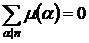 .
.
Например, n=100, aÎ{1, 2, 4, 5, 10, 20, 25, 50, 100}.
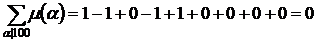 .
.
Производящие функции
Двенадцатиричный путь
(из тетради)
КОМБИНАТОРИКА
Некоторые сведения из теории множеств
Множество – любое собрание объектов, определённых и хорошо различимых нашей интуицией или интеллектом, мыслимое как единое целое (Георг Кантор, 1872 г.).
Множества обозначаются большими буквами, элементы множества – малыми.
Принадлежность. Если x принадлежит множеству S (x является элементом S), то это обозначается xÎS. Если x не принадлежит S – xÏS.
Пример: S={a,b,c}, aÎS, bÎS, cÎS, dÏS.
Подмножество. Отношение включения.Если все элементы множества А принадлежат множеству B, то А – подмножество множества B. Это обозначается так: АÍB (А не строго включается в B). Если при этом в B есть элементы, не принадлежащие А, то это обозначают АÌB (А строго включается в B; A – собственное подмножество B).
Универсальное множество – множество всех элементов какого-либо определённого типа.
Пустое множество (Æ) – множество, не содержащее ни одного элемента. По определению, пустое множество является подмножеством любого множества. (" S : ÆÍS).
Мощность множества. Для конечных множеств мощность –количество элементов во множестве. Мощность множества S обозначается |S|. Например, S={a, b, c}, |S|=3.
Множества называются равномощными (эквивалентными), если их мощность равны.
Операции над множествами
Пусть заданы множества A и B.
Объединениемножеств A и B – множество АÈВ={x : xÎA или xÎB} (объединение содержит элементы, которые есть или в A, или в B, или в том и другом множестве). (нарисовать с помощью кругов Эйлера). АÈВ= BÈA.
Пересечениемножеств A и B – множество АÇВ={x : xÎA и xÎB} (пересечение содержит элементы, которые есть одновременно и в A, и в B. (нарисовать). АÇВ= BÇA.
Дополнение до универсальногомножества. Если В – универсальное множество, и АÍВ, то дополнение 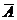 ={x : xÎB и xÏA}. (нарисовать).
={x : xÎB и xÏA}. (нарисовать).
Произведениемножеств A и B – множество AxB={<x, y> : xÎA, yÎB} (множество всех пар, первый элемент которых принадлежит множеству A, второй элемент – множеству B). Мощность произведения AxB равна произведению мощностей A и B (|AxB|=|A|*|B|). Произведение BxA не равно AxB, но их мощности совпадают (BxA ¹ AxB, но |BxA| = |AxB|).
Пример: A={a, b, c}, B={c, d}, |A|=3, |B|=2.
АÈВ={a, b, c, d}, АÇВ={c}, AxB={<a,c>, <a,d>, <b,c>, <b,d>, <c,c>, <c,d>}, BxA={<c,a>, <c,b>, <c,c>, <d,a>, <d,b>, <d,c>}, |AxB|=6, |BxA|=6.
Оператор (функция) – правило, определяющее отображение некоторого множества X в некоторое множество Y. Обозначение: F : X®Y.
Пример: X={a, b, c, d}, Y={▲, ●, ■}. Возможный вариант функции: f(a)=■, f(b)=●, f(c)=■, f(d)=▲.
 X Y a ▲ b ● c ■ d X Y a ▲ b ● c ■ d |
Дискретное множество – множество, состоящее из изолированных точек (т.е. множество, не имеющее предельных точек). Например, множество натуральных чисел – дискретное множество, а множество действительных чисел – непрерывное множество.
Дискретная математика изучает свойства дискретных множеств и определённых на них операторов. Непрерывными множествами занимается математический анализ.
Лекция 1.
