Общая информация об алгоритмах сортировки

Квадратичные и субквадратичные алгоритмы

Сортировка выбором (select)

Идея метода состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке.

Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.

На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рисунке ниже.

Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] (выделена курсивом) является упорядоченной. Таким образом, на (n-1)-м шаге вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево.

template<class T>

void selectSort(T a[], long size) {

long i, j, k;

T x;

for( i=0; i < size; i++) { // i - номер текущего шага

k=i; x=a[i];

for( j=i+1; j < size; j++) // цикл выбора наименьшего элемента

if ( a[j] < x ) {

k=j; x=a[j]; // k - индекс наименьшего элемента

}

a[k] = a[i]; a[i] = x; // меняем местами наименьший с a[i]

}

}

Для нахождения наименьшего элемента из n+1 рассматримаемых алгоритм совершает n сравнений. С учетом того, что количество рассматриваемых на очередном шаге элементов уменьшается на единицу, общее количество операций:

n + (n-1) + (n-2) + (n-3) + ... + 1 = 1/2 * ( n²+n ) = Theta(n²).

Таким образом, так как число обменов всегда будет меньше числа сравнений, время сортировки растет квадратично относительно количества элементов.

Алгоритм не использует дополнительной памяти: все операции происходят "на месте".

Устойчив ли этот метод ? Прежде, чем читать далее, попробуйте получить ответ самостоятельно.

Рассмотрим последовательность из трех элементов, каждый из которых имеет два поля, а сортировка идет по первому из них.

Результат ее сортировки можно увидеть уже после шага 0, так как больше обменов не будет. Порядок ключей 2a, 2b был изменен на 2b, 2a, так что метод неустойчив.

Если входная последовательность почти упорядочена, то сравнений будет столько же, значит алгоритм ведет себя неестественно.

Сортировка Шелла (shell)

Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.

Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

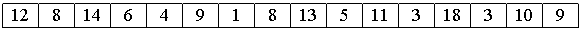
1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

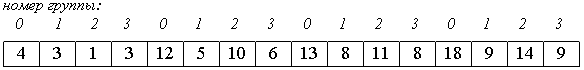
В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.

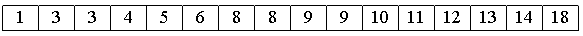
Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?

Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.

Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.

Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор, особенно, когда количество элементов - степень двойки. Однако гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид

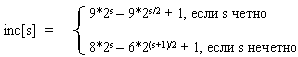
При использовании таких приращений среднее количество операций: O(n^7/6), в худшем случае - порядка O(n^4/3).

Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке.
При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.

int increment(long inc[], long size) {

int p1, p2, p3, s;

p1 = p2 = p3 = 1;

s = -1;

do {

if (++s % 2) {

inc[s] = 8*p1 - 6*p2 + 1;

} else {

inc[s] = 9*p1 - 9*p3 + 1;

p2 *= 2;

p3 *= 2;

}

p1 *= 2;

} while(3*inc[s] < size);

return s > 0 ? --s : 0;

}

template<class T>

void shellSort(T a[], long size) {

long inc, i, j, seq[40];

int s;

// вычисление последовательности приращений

s = increment(seq, size);

while (s >= 0) {

// сортировка вставками с инкрементами inc[]

inc = seq[s--];

for (i = inc; i < size; i++) {

T temp = a[i];

for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc)

a[j+inc] = a[j];

a[j+inc] = temp;

}

}

}

Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size.

Быстрая сортировка (quick)

"Быстрая сортировка", хоть и была разработана более 40 лет назад, является наиболее широко применяемым и одним их самых эффективных алгоритмов.

Метод основан на подходе "разделяй-и-властвуй". Общая схема такова:

1. из массива выбирается некоторый опорный элемент a[i],
2. запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо,
3. теперь массив состоит из двух подмножеств, причем левое меньше, либо равно правого,
   
4. для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

В конце получится полностью отсортированная последовательность.

Рассмотрим алгоритм подробнее.

Разделение массива

На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение.

1. Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности.
2. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.
3. Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам...
4. Повторяем шаг 3, пока i <= j.

Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3].

Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено.

Общий алгоритм

Псевдокод.

quickSort ( массив a, верхняя граница N ) { Выбрать опорный элемент p - середину массива Разделить массив по этому элементу Если подмассив слева от p содержит более одного элемента, вызвать quickSort для него. Если подмассив справа от p содержит более одного элемента, вызвать quickSort для него. }

Реализация на Си.

template<class T>void quickSortR(T* a, long N) {// На входе - массив a[], a[N] - его последний элемент. long i = 0, j = N; // поставить указатели на исходные места T temp, p; p = a[ N>>1 ]; // центральный элемент // процедура разделения do { while ( a[i] < p ) i++; while ( a[j] > p ) j--; if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while ( i<=j ); // рекурсивные вызовы, если есть, что сортировать if ( j > 0 ) quickSortR(a, j); if ( N > i ) quickSortR(a+i, N-i);}

Каждое разделение требует, очевидно, Theta(n) операций. Количество шагов деления(глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: O(n log n), что и имеет место на практике.

Однако, возможен случай таких входных данных, на которых алгоритм будет работать за O(n²) операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге... Вообще говоря, малореальная ситуация.

Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части.

Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет O(log n), а данные о рекурсивных подвызовах каждый раз добавляются в стек.

Модификации кода и метода

1. Из-за рекурсии и других "накладных расходов" Quicksort может оказаться не столь уж быстрой для коротких массивов. Поэтому, если в массиве меньше CUTOFF элементов (константа зависит от реализации, обычно равна от 3 до 40), вызывается сортировка вставками. Увеличение скорости может составлять до 15%.

Для проведения метода в жизнь можно модифицировать функцию quickSortR, заменив последние 2 строки на

if ( j > CUTOFF ) quickSortR(a, j); if ( N > i + CUTOFF ) quickSortR(a+i, N-i);

Таким образом, массивы из CUTOFF элементов и меньше досортировываться не будут, и в конце работы quickSortR() массив разделится на последовательные части из <=CUTOFF элементов, отсортированные друг относительно друга. Близкие элементы имеют близкие позиции, поэтому, аналогично сортировке Шелла, вызывается insertSort(), которая доводит процесс до конца.

template<class T>void qsortR(T *a, long size) { quickSortR(a, size-1); insertSort(a, size); // insertSortGuarded быстрее, но нужна функция setmax()}

1. В случае явной рекурсии, как в программе выше, в стеке сохраняются не только границы подмассивов, но и ряд совершенно ненужных параметров, таких как локальные переменные. Если эмулировать стек программно, его размер можно уменьшить в несколько раз.
2. Чем на более равные части будет делиться массив - тем лучше. Потому в качестве опорного целесообразно брать средний из трех, а если массив достаточно велик - то из девяти произвольных элементов.
3. Пусть входные последовательности очень плохи для алгоритма. Например, их специально подбирают, чтобы средний элемент оказывался каждый раз минимумом. Как сделать QuickSort устойчивой к такому "саботажу" ? Очень просто - выбирать в качестве опорного случайный элемент входного массива. Тогда любые неприятные закономерности во входном потоке будут нейтрализованы. Другой вариант - переставить перед сортировкой элементы массива случайным образом.
4. Быструю сортировку можно использовать и для двусвязных списков. Единственная проблема при этом - отсутствие непосредственного доступа к случайному элементу. Так что в качестве опорного приходится выбирать первый элемент, и либо надеяться на хорошие исходные данные, либо случайным образом переставить элементы перед сортировкой.

Рассмотрим наихудший случай, когда случайно выбираемые опорные элементы оказались очень плохими(близкими к экстремумам). Вероятность этого чрезвычайно мала, уже при n = 1024 она меньше 2^-50, так что интерес скорее теоретический, нежели практический. Однако, поведение "быстрой сортировки" является "эталоном" для аналогично реализованных алгоритмов типа "разделяй-и-властвуй". Не везде можно свести вероятность худшего случая практически к нулю, поэтому такая ситуация заслуживает изучения.

Пусть, для определенности, каждый раз выбирается наименьший элемент a_min . Тогда процедура разделения переместит этот элемент в начало массива и на следующий уровень рекурсии отправятся две части: одна из единственного элемента a_min, другая содержит остальные n-1 элемента массива. Затем процесс повторится для части из (n-1) элементов.. И так далее..
При использовании рекурсивного кода, подобного написанному выше, это будет означать n вложенных рекурсивных вызовов функции quickSort.
Каждый рекурсивный вызов означает сохранение информации о текущем положении дел. Таким образом, сортировка требует O(n) дополнительной памяти.. И не где-нибудь, а в стеке. При достаточно большом n такое требование может привести к непредсказуемым последствиям.

Для исключения подобной ситуации можно заменить рекурсию на итерации, реализовав стек на основе массива. Процедура разделения будет выполняться в виде цикла.
Каждый раз, когда массив делится на две части, в стек будет направляться запрос на сортировку большей из них, а меньшая будет обрабатываться на следующей итерации. Запросы будут выбираться из стека по мере освобождения процедуры разделения от текущих задач. Сортировка заканчивает свою работу, когда запросы кончаются.

Псевдокод.

Итеративная QuickSort (массив a, размер size) {Положить в стек запрос на сортировку массива от 0 до size-1. do { Взять границы lb и ub текущего массива из стека. do { 1. Произвести операцию разделения над текущим массивом a[lb..ub]. 2. Отправить границы большей из получившихся частей в стек. 3. Передвинуть границы ub, lb чтобы они указывали на меньшую часть. } пока меньшая часть состоит из двух или более элементов } пока в стеке есть запросы}

Реализация на Си.

#define MAXSTACK 2048 // максимальный размер стека template<class T>void qSortI(T a[], long size) { long i, j; // указатели, участвующие в разделении long lb, ub; // границы сортируемого в цикле фрагмента long lbstack[MAXSTACK], ubstack[MAXSTACK]; // стек запросов // каждый запрос задается парой значений, // а именно: левой(lbstack) и правой(ubstack) // границами промежутка long stackpos = 1; // текущая позиция стека long ppos; // середина массива T pivot; // опорный элемент T temp; lbstack[1] = 0; ubstack[1] = size-1; do { // Взять границы lb и ub текущего массива из стека. lb = lbstack[ stackpos ]; ub = ubstack[ stackpos ]; stackpos--; do { // Шаг 1. Разделение по элементу pivot ppos = ( lb + ub ) >> 1; i = lb; j = ub; pivot = a[ppos]; do { while ( a[i] < pivot ) i++; while ( pivot < a[j] ) j--; if ( i <= j ) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while ( i <= j ); // Сейчас указатель i указывает на начало правого подмассива, // j - на конец левого (см. иллюстрацию выше), lb ? j ? i ? ub. // Возможен случай, когда указатель i или j выходит за границу массива // Шаги 2, 3. Отправляем большую часть в стек и двигаем lb,ub if ( i < ppos ) { // правая часть больше if ( i < ub ) { // если в ней больше 1 элемента - нужно stackpos++; // сортировать, запрос в стек lbstack[ stackpos ] = i; ubstack[ stackpos ] = ub; } ub = j; // следующая итерация разделения // будет работать с левой частью } else { // левая часть больше if ( j > lb ) { stackpos++; lbstack[ stackpos ] = lb; ubstack[ stackpos ] = j; } lb = i; } } while ( lb < ub ); // пока в меньшей части более 1 элемента } while ( stackpos != 0 ); // пока есть запросы в стеке}

Размер стека при такой реализации всегда имеет порядок O(log n), так что указанного в MAXSTACK значения хватает с лихвой.

Сортировка подсчетом

Пусть у нас есть массив source из n десятичных цифр ( m = 10 ).
Например, source[7] = { 7, 9, 8, 5, 4, 7, 7 }, n=7. Здесь положим const k=1.

1. Создать массив count из m элементов(счетчиков).
2. Присвоить count[i] количество элементов source, равных i. Для этого:

1. проинициализовать count[] нулями,
2. пройти по source от начала до конца, для каждого числа увеличивая элемент count с соответствующим номером.

c. for( i=0; i<n; i++) count [ source[i] ]++

В нашем примере count[] = { 0, 0, 0, 0, 1, 1, 0, 3, 1, 1 }

1. Присвоить count[i] значение, равное сумме всех элементов до данного:
   count[i] = count[0]+count[1]+...count[i-1].
   В нашем примере count[] = { 0, 0, 0, 0, 1, 2, 2, 2, 5, 6 }
   Эта сумма является количеством чисел исходного массива, меньших i.
2. Произвести окончательную расстановку.

Для каждого числа source[i] мы знаем, сколько чисел меньше него - это значение хранится в count[ source[i] ]. Таким образом, нам известно окончательное место числа в упорядоченном массиве: если есть K чисел меньше данного, то оно должно стоять на на позиции K+1.
Осуществляем проход по массиву source слева направо, одновременно заполняя выходной массив dest:

for ( i=0; i<n; i++ ) { c = source[i]; dest[ count[c] ] = c; count[c]++; // для повторяющихся чисел }

Таким образом, число c=source[i] ставится на место count[c]. На этот случай, если числа повторяются в массиве, предусмотрен оператор count[c]++, который увеличивает значение позиции для следующего числа c, если таковое будет.

Циклы занимают (n + m) времени. Столько же требуется памяти.

Итак, мы научились за (n + m) сортировать цифры. А от цифр до строк и чисел - 1 шаг. Пусть у нас в каждом ключе k цифр ( m = 10 ). Аналогично случаю со списками отсортируем их в несколько проходов от младшего разряда к старшему.

Общее количество операций, таким образом, ( k(n+m) ), при используемой дополнительно памяти (n+m). Эта схема допускает небольшую оптимизацию. Заметим, что сортировка по каждому байту состоит из 2 проходов по всему массиву: на первом шаге и на четвертом. Однако, можно создать сразу все массивы count[] (по одному на каждую позицию) за один проход. Неважно, как расположены числа - счетчики не меняются, поэтому это изменение корректно.
Таким образом, первый шаг будет выполняться один раз за всю сортировку, а значит, общее количество проходов изменится с 2k на k+1.

Формат IEEE-754

Особенно подходящим местом применения radixSort является компьютерная графика. Есть много координат, которые необходимо отсортировать, причем с наибольшей скоростью. Поэтому было бы очень удобно распространить возможности процедуры на числа с плавающей точкой.

С другой стороны, существует несколько стандартов для представления таких чисел. Наиболее известным следует признать IEEE-754, который используется в IBM PC, Macintosh, Dreamcast и ряде других систем. Зафиксировав формат представления числа, уже можно модифицировать соответствующим образом сортировку.

Любое число можно записать в системе с основанием BASE как M*BASEn, где |M|<BASE. Например, 47110 = 4.7110 * 102, 6.510 = 6.510*100, -0.003210 = -3.210 * 10-3.
В двоичной системе можно дополнительно сделать первую цифру M равной 1: 101.012 = 1.01012*22, -0.000011 = -1.12*2-5

Такая запись называется нормализованной. M называется мантиссой, n - порядком числа. Стандарт IEEE-754 предполагает запись числа в виде [знак][порядок][мантисса]. Различным форматам соответствует свой размер каждого из полей. Для чисел одинарной точности(float) это 1 бит под знак, 8 под порядок и 23 на мантиссу. Числа двойной точности(double) имеют порядок из 11 бит, мантиссу из 52 бит. Некоторые процессоры(например, 0x86) поддерживают расширенную точность(long double).

тип/бит	[Знак]	[Порядок]	[Мантисса]	[Смещение]
float
double

Рассмотрим числа одинарной точности(float).
Как и в целых числах, значение знакового бита 0 означает, что число положительное, значение 1 - число отрицательное.
Так как первая цифра мантиссы всегда равна 1, то хранится только ее дробная часть. То есть, если M=1.010112, то [Мантисса]= 010112. Если M=1.10112, то [Мантисса]=10112. Таким образом в 23 битах хранится мантисса до 24 бит длиной. Чтобы получить из поля [Мантисса] правильное значение M необходимо мысленно прибавить к его значению единицу с точкой.

Для удобства представления отрицательного порядка в соответствующем поле реально хранится порядок+смещение. Например, если n=0, то [Порядок]=127. Если n=-7, то [Порядок]=120. Таким образом, его значение всегда неотрицательно.

Таким образом, общая формула по получению обычной записи числа из формата IEEE-754:

N = (-1)[Знак] * 1.[Мантисса] * 2[Порядок]-127 (нормализованная запись, 1)

Для 10.2510 = 1010.012 = +1.01001 * 23 соответствующие значения будут [Знак]=0 (+) , [Порядок] = 130(=3+127), [Мантисса] = 010012.

При значениях [Порядок]=1...254 эта система позволяет представлять числа приблизительно от +-3,39*10-38 до +-3,39*10+38.

Особым образом обрабатываются [Порядок]=0 и [Порядок]=255.

Если [Порядок]=0, но мантисса отлична от нуля, то перед ее началом необходимо ставить вместо единицы ноль с точкой. Так что формула меняется на

N = (-1)[Знак] * 0.[Мантисса] * 2-126 (денормализованная запись, 2)

Это расширяет интервал представления чисел до +-1,18*10-38. ... +-3,39*10+38

[Порядок]=0 [Мантисса]=0 обозначают ноль. Возможно существование двух нулей: +0 и -0, которые отличаются битом знака, но при операциях ведут себя одинаково. В этом смысле можно интерпретировать ноль как особое денормализованное число со специальным порядком.

Значение [Порядок]=255(все единицы) зарезервировано для специальных целей, более подробно описанных в стандарте. Такое поле в зависимости от мантиссы обозначает одно из трех специальных "нечисел", которые обозначают как Inf, NaN, Ind, и может появиться в результате ошибок в вычислениях и при переполнении.

Числа двойной точности устроены полностью аналогичным образом, к порядку прибавляется не 127, а 1023. Увеличение длин соответствующих полей позволяет хранить числа от 10-323.3 до 10308.3, значение [Порядок]=2047(все единицы) зарезервировано под "нечисла".

Результаты тестирования

На диаграммах изображены результаты сравнений поразрядной сортировки (синяя линия) и быстрой(розовая линия), причем использовалась функция sort() из библиотеки STL.

• short
  Благодаря малой разрядности и простоте внутренних циклов, поразрядная перегнала быструю сортировку уже на 100 элементах.
• long
  При переходе к типу long произошло двукратное увеличение количества проходов RadixPass, поэтому худшая асимптотика быстрой сортировки показала себя лишь после 600 элементов, где она начала отставать.
• float
  По графику видно, что для этого типа поразрядная сортировка оказалась гораздо эффективнее, нежели для long. В чем дело, ведь размер одинаков - 4 байта ?
  Оказывается, на типе float резко возрастает время работы быстрой сортировки. Возможно, это связано с тем, что процессор, прежде чем делать какие-либо операции, переводит его в double, а потом работает с этим типом, который 2 раза больше по размеру.. Так или иначе, быстрая сортировка стала работать в 2 раза медленнее, и поразрядная вышла вперед после 100 элементов.
• double
  График показан с десятикратным увеличением.
  Размер типа увеличился в 2 раза, поэтому для небольших n поразрядная сортировка, конечно, отстает, но перегоняет быструю на массивах из нескольких тысяч элементов. Небольшое преимущество radixSort длится приблизительно до 16000 элементов, когда данные начинают вылезать за пределы кэша. Соответственно, начинает играть роль медленный непоследовательный доступ (с шагами по 8 байт) к основной памяти.. В результате поразрядная сортировка снова выбивается вперед лишь после 500000 элементов.

Общая информация об алгоритмах сортировки

Пусть есть последовательность a₀, a₁... a_n и функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: a_i <= a_i+1, для всех i от 0 до n.

Возможна ситуация, когда элементы состоят из нескольких полей:

struct element { field x; field y; }

Если значение функции сравнения зависит только от поля x, то x называют ключом, по которому производится сортировка. На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.

Пожалуй, никакая другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Существует ли некий "универсальный", наилучший алгоритм ? Вообще говоря, нет. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом.

Для того, чтобы обоснованно сделать такой выбор, рассмотрим параметры, по которым будет производиться оценка алгоритмов.

1. Время сортировки - основной параметр, характеризующий быстродействие алгоритма.
2. Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
3. Устойчивость - устойчивая сортировка не меняет взаимного расположения равных элементов. Такое свойство может быть очень полезным, если они состоят из нескольких полей, как на рис. 1, а сортировка происходит по одному из них, например, по x.

Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".

Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось.

1. Естественность поведения - эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

Еще одним важным свойством алгоритма является его сфера применения. Здесь основных позиций две:

• внутренние сортировки работают с данным в оперативной памяти с произвольным доступом;
• внешние сортировки упорядочивают информацию, расположенную на внешних носителях. Это накладывает некоторые дополнительные ограничения на алгоритм:
• доступ к носителю осуществляется последовательным образом: в каждый момент времени можно считать или записать только элемент, следующий за текущим
• объем данных не позволяет им разместиться в ОЗУ

Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.

Данный класс алгоритмов делится на два основных подкласса:

Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно сортируются на том же месте, без дополнительных затрат.

Внешняя сортировка оперирует с запоминающими устройствами большого объема, но с доступом не произвольным, а последовательным (сортировка файлов), т.е в данный момент мы 'видим' только один элемент, а затраты на перемотку по сравнению с памятью неоправданно велики . Это приводит к специальным методам сортировки, обычно использующим дополнительное дисковое пространство.

Основные методы сортировки

Статьи ниже являются частями одной большой, так что в последующих может использоваться информация из предыдущих. В программах используются переопределения:

typedef double real;typedef unsigned long ulong;typedef unsigned short ushort;typedef unsigned char uchar;

Под переменной size принимается количество элементов в массиве, а для обозначения индекса последнего элемента используется N. Очевидно, size=N+1.