Вариационные и атрибутивные ряды распределения

В зависимости от признака различают:

· Вариационные ряды (количественный признак)

· Атрибутивные ряды (качественный, (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).

Основными элементами вариационного ряда являются:

· Значение признака (варианта, Х)

· Частота fi - число ед. совокупности с данным значением признака

· Частостьw – частоты выраженные в долях ед. или в %

· Накопленная частота s – частота нарастающим итогом

· НакопленнаячастостьW – частость нарастающим итогом

Для графического изображения дискретных вариационных рядов распрееления используют кривые (полигон) по оси OX-значение признака, по оси OY – частоты

Для интервальных используется гистограмма

. Абсолютные показатели:
а) размах вариации;
б) дисперсия;
в) среднее квадратическое отклонение;
г) среднее линейное отклонение.
2. Относительные показатели:
а) линейный коэффициент вариации;
б) коэффициент асциляции;
в) коэффициент детерминации;
г) эмпирическое корелляционное отношение.

Средние величины

Это количественная характеристика признака статистической совокупности, отражающая уровень этого признака в расчете на ед. совокупности.

Степенные средние

· Средняя арифметическая (для усреднения абсолютных величин)

А) простая (по не сгруппированным данным) 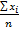б) взвешенная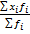

· Средняя гармоническая (когда необходимо при осреднении чтобы неизменной оставалась сумма величин обратных индивидуальным значениям признака)

А) простая 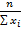б) взвешенная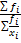

· Средняя геометрическая (при анализе темпов роста экономических показателей)

· Средняя кубическая (при расчете с величинами кубических функций)

А) простая 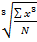б) взвешенная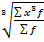

· Средняя хронологическая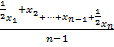

Структурные средние

Квантили - значение признака занимающее определенное место в упорядоченной по данной совокупности признаку)

· Мода ( значение признака наиболее часто встречающегося в изучаемой совокупности)

Для дискретного ряда = значению признака имеющего наибольшую частоту

Для интервального ряда: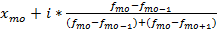

· Медиана ( значение признака приходящегося на середину упорядоченной совокупности)

Для дискретного - при нечетном количестве значений = середине ряда, при четном = ср. арифметической из 2х средних.

Для интервального: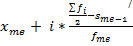

Показатели вариации

Вариация – это количественное различие значений одного и того же признака у отдельных единиц совокупности.

Задачи:

· Построение вариационных рядов распределения по количественному признаку

· Определение среднего значения и степенных средних

· Определение размера интенсивности и размера вариации

· Определение характеристик формы распределения

Изменчивость явления в статистическом анализе отображается с помощью характеристик, называемых системой показателей вариации.

1. Абсолютные показатели:

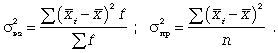
а) размах вариации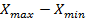
б) дисперсия
в) среднее квадратическое отклонение

Среднее квадратическое отклонение простое .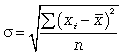

Среднее квадратическое взвешенное .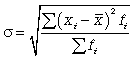
г) среднее линейное отклонение

Формула среднего линейного отклонения (простая) .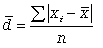
Формула среднего линейного отклонения (взвешенная) .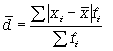
2. Относительные показатели:

а) линейный коэффициент вариации;
б) коэффициент асциляции
в) коэффициент детерминации;
г) эмпирическое корелляционное отношение.
С помощью относительных показателей вариации решаются следующие задачи:
1) сравнение степени вариации в процентах различных признаков в одной и той же совокупности;
2) сравнение степени вариации одного и того же признака в различных совокупностях.