Сравнение распределений в терминах риска и доходности
Будем считать, что все допустимые распределения удовлетворяют следующим условиям: F(0) = 0 и F(x) = 1 для некоторого х.
Будем говорить, что имеет место стохастическое доминирование[3] первой степени распределения F() над распределением G(), если для любой неубывающей функции u выполняется следующее соотношение: 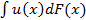
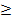
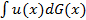 .
.
Стохастическое доминирование первой степени распределения F() над G() имеет место тогда и только тогда, когда F(x) 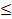 G(x) для любого x.
G(x) для любого x.
Критерий стохастического доминирования второй степени
Пусть распределение F() и G() характеризуются одинаковым математическим ожиданием. Стохастическое доминирование второй степени распределения F() над распределением G() имеет место тогда и только тогда, когда 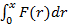
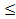
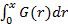 . для любого х.
. для любого х.
[1] Аффинные преобразования,точечные взаимно однозначные отображения плоскости (пространства) на себя, при которых прямые переходят в прямые. Частным случаем аффинных преобразований являются движения и преобразования подобия.
[2] (от лат. contingere – случаться) случайность как противоположность необходимости.
[3] Критерий стохастического доминирования второго порядка основан на сравнивании не функций распределения доходности портфелей, а интегралов от этих функций, т.е. площадей под функциями распределения. Определим зависимость величины данной площади от значения г как накопленную функцию распределения. Тогда можно сказать, что первый портфель предпочтительнее второго, если накопленная функций распределения его доходности никогда не превосходит, и по крайней мере в одном случае меньше, накопленной функции распределения второго портфеля. Доминирование второго порядка определяется для инвестора не склонного к риску, поэтому оно учитывает тот факт, что ценность единицы богатства для него выше для небольшого уровня богатства и уменьшается с его ростом. В результате инвестор должен в большей степени предпочесть портфель, для которого существует меньшая вероятность принести меньший доход на более нижнем участке распределения доходности, чем на более верхнем. Другими словами, инвестор больше теряет полезности от потери богатства на более нижнем отрезке распределения доходности, чем на более верхнем. В рамках стохастического доминирования второго порядка рассматривается инвестор не склонный к риску, поэтому оно имеет отношение к дисперсии доходности портфелей.
Как следует из условия доминирования второго порядка, доминирование первого порядка одного портфеля над другим автоматически предполагает его стохастическое доминирование и второго порядка. Таким образом, условие сто-хастического доминирования второго порядка является более слабым условием.
Буренин А.М, «Управление портфелем ценных бумаг»
