Взаимное расположение точки и прямой

Точка может находиться либо на прямой, либо внееё.

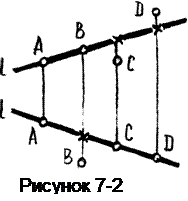
а) Если точка находится напрямой, тогда на основании свойства принадлежности её проекции будут принадлежать проекциям прямой – точка А (рисунок 7-2);

б) Если же точка расположена внепрямой, то тогда хотя бы на одном из видов точка не будет находиться на прямой:

· точка В на виде сверху не лежит на прямой l, а находится ближе, чем фронтально-конкурирующая с ней точка, отмеченная крестиком; следовательно точка В находится перед прямой l;

· точка С, как это следует из вида спереди, находится нижепрямой l, т.к. она расположена ниже горизонтально-конкурирующей с ней точки, отмеченной крестиком и лежащей на прямой;

· анализируя положение точки D относительно прямой l, приходим к выводу, что точка D находится над прямой l, что определяется по положению точки D на виде спереди. По виду сверху отмечаем, что точка D находится за прямой l.

Определить взаимное положение точки и прямой профильного положения р по двум видам не представляется возможным, т.к. такая прямая на видах спереди и сверху совпадает с линиями связи по направлению (рисунок 7-3).

Получить ответ можно с помощью построения профильной проекции (вида слева).

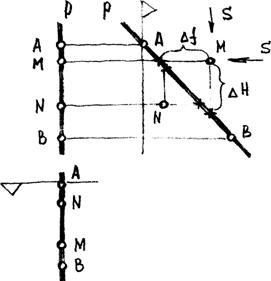Так по виду слева определяем, что т. М находится передпрямой (Δf) и над ней (ΔН), т.к. она лежит ближе фронтально-конкурирующей и выше горизонтально -конкурирующих точек, отмеченных крестиками.

Точка N находится ниже (под) прямой l и за (дальше) неё.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ПЛОСКОСТИ

Может быть два варианта:

· точка находится в плоскости;

· точка находится вне плоскости.

Точка находится в плоскости, если она принадлежит какой-нибудь прямой этой плоскости.

Следовательно, чтобы построить точку на плоскости, необходимо сначала на этой плоскости построить произвольную прямую линию (или взять уже имеющуюся) и на ней взять точку.

Плоскость частного положения

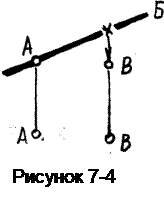Если точка находится в плоскостичастного положения (наклонной, вертикальной, профильно-проецирующей), то построение ее облегчается. В этом случае точка на одном из видов будет находиться на изображении плоскости, а на другом виде положение ее может быть произвольным (рисунок 7-4). Здесь показана т. А принадлежащая наклонной плоскости Б, т.к. на виде спереди она находится на прямой, являющейся изображением плоскости; а на виде сверху положение точки взято на линии связи произвольно.

Точка В находится под плоскостью, т.к. она лежит ниже отмеченной крестиком точки, с которой она горизонтально конкурирует,

Плоскость общего положения

Несколько сложнее построить на комплексном чертеже точку, принадлежащую плоскости общегоположения.

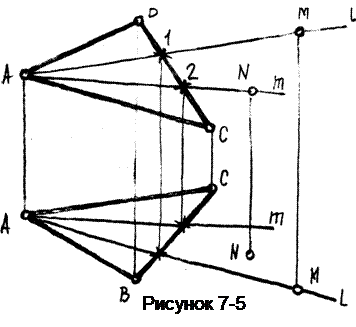Пусть задана плоскость Б(ΔАВС), (рисунок 7-5). Чтобы построить на чертеже какую-нибудь точку лежащую в плоскости Б, проведена произвольная прямая l явно принадлежащая плоскости (т.к. проходит через две точки плоскости А и 1). Затем на этой прямой взята т. М (свойство принадлежности).

Рассмотрим обратную задачу. Пусть заданы два вида точки N. Нужно определить положение т. N относительно плоскости.

Для решения этой задачи нужно на плоскости провести вспомогательную прямую, конкурирующую с данной точкой на любом из видов (например на виде спереди, как на рисунке 7-5) и определить взаимное положение данной точки N и прямой.

Итак, проведем фронтально-конкурирующую с точкой N прямую m, положение которой определено точками плоскости А и 2. По глубине точки N определяем, что она находится перед прямой l и, следовательно, перед плоскостью.

Поскольку плоскость Б - нисходящая (определяем по разным направлениям обхода на видах), и, учитывая, что т. N находится перед плоскостью, то она в то же время будет находиться и под плоскостью.