Взаимное положение двух точек.
ЛЕКЦИЯ №7
ПОЗИЦИОННЫЕ ЗАДАЧИ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ТОЧЕК.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ПЛОСКОСТИ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ.
Позиционные задачи– это задачи, в которых определяется взаимное расположение различных геометрических фигур относительно друг друга.
Различают прямые и обратные позиционные задачи:
· прямые– задачи на взаимопринадлежность (построение точки на линии или поверхности, проведение линии на поверхности или поверхности через заданные линии, задачи на пересечение);
· обратные – в которых определяется взаимное расположение точек, линий, плоскостей.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ТОЧЕК
Рассмотрим возможные варианты взаимного расположения двух точек (рисунок 7-1).
а) б) в) г)
А=В А А=В А
∆Н
В В
∆р
В А
А=В А=В А ∆f В
Рисунок 7-1
а) две точки в пространстве могут либо совпадать, либо не совпадать. Если две точки совпадают, то на видах спереди и сверху их проекции совпадают (рисунок 7-1а).
Если же точки не совпадают, то их проекции не совпадают либо на виде спереди (7-1б), либо на виде сверху (7-1в), либо на двух видах одновременно (7-1г).
б) Точки, которые совпадают на виде сверху (на горизонтальной проекции) называют горизонтально-конкурирующими. На рисунке7-1б точка А находится выше точки В и точно над ней, поэтому на виде спереди обе точки видимы, а на виде сверху видна точка А, имеющая большую высоту.
в) Точки, которые совпадают на виде спереди (на фронтальной проекции) называют фронтально-конкурирующими. На виде сверху обе точки видимы, а на виде спереди видна та из них, что ближе к наблюдателю, т.е. точка А.
г) По рисунку 7-1г определяем, что точка А выше точки В на величину ΔН; по виду сверху отмечаем, что от наблюдателя точка А дальше точки В на величину Δf ; на обоих видах определяется, что точка А левее точки В на величину Δр.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ПЛОСКОСТИ
Может быть два варианта:
· точка находится в плоскости;
· точка находится вне плоскости.
Точка находится в плоскости, если она принадлежит какой-нибудь прямой этой плоскости.
Следовательно, чтобы построить точку на плоскости, необходимо сначала на этой плоскости построить произвольную прямую линию (или взять уже имеющуюся) и на ней взять точку.
Плоскость частного положения
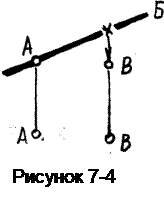Если точка находится в плоскостичастного положения (наклонной, вертикальной, профильно-проецирующей), то построение ее облегчается. В этом случае точка на одном из видов будет находиться на изображении плоскости, а на другом виде положение ее может быть произвольным (рисунок 7-4). Здесь показана т. А принадлежащая наклонной плоскости Б, т.к. на виде спереди она находится на прямой, являющейся изображением плоскости; а на виде сверху положение точки взято на линии связи произвольно.
Точка В находится под плоскостью, т.к. она лежит ниже отмеченной крестиком точки, с которой она горизонтально конкурирует,
Плоскость общего положения
Несколько сложнее построить на комплексном чертеже точку, принадлежащую плоскости общегоположения.
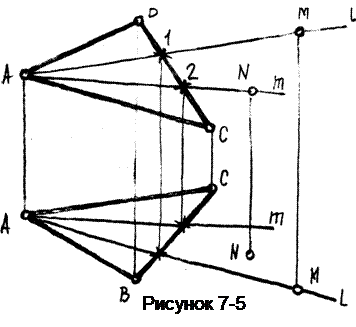Пусть задана плоскость Б(ΔАВС), (рисунок 7-5). Чтобы построить на чертеже какую-нибудь точку лежащую в плоскости Б, проведена произвольная прямая l явно принадлежащая плоскости (т.к. проходит через две точки плоскости А и 1). Затем на этой прямой взята т. М (свойство принадлежности).
Рассмотрим обратную задачу. Пусть заданы два вида точки N. Нужно определить положение т. N относительно плоскости.
Для решения этой задачи нужно на плоскости провести вспомогательную прямую, конкурирующую с данной точкой на любом из видов (например на виде спереди, как на рисунке 7-5) и определить взаимное положение данной точки N и прямой.
Итак, проведем фронтально-конкурирующую с точкой N прямую m, положение которой определено точками плоскости А и 2. По глубине точки N определяем, что она находится перед прямой l и, следовательно, перед плоскостью.
Поскольку плоскость Б - нисходящая (определяем по разным направлениям обхода на видах), и, учитывая, что т. N находится перед плоскостью, то она в то же время будет находиться и под плоскостью.
ЛЕКЦИЯ №7
ПОЗИЦИОННЫЕ ЗАДАЧИ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ТОЧЕК.