Оптимизация инвестиционного портфеля по методу У. Шарпа

Для того чтобы выбрать оптимальный портфель, инвестор должен нарисовать кривые безразличия, как это было показано ранее (рис. 3), а затем приступить к анализу всех портфелей, лежащих выше и левее всех остальных кривых безразличия с учетом ожидаемой доходности, стандартного отклонения и ковариации. Если иметь в портфеле несколько ценных бумаг, то это действительно просто сделать. Но когда формируется портфель, состоящий из сотен, а порой из тысячи ценных бумаг, то возникает проблема выбора из эффективного множества портфеля, представляющего собой оптимальную комбинацию доходности и стандартного отклонения, а также предпочтений инвестора относительно риска и доходности.

Рассмотрим ряд моделей, используемых для формирования портфелей.

Представим себе, что доходность обыкновенной акции за данный период времени связана с индексом РТС. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции, а с падением рыночного индекса, вероятно, будет падать и цена акции. Эту взаимосвязь отражает рыночная модель (market model):

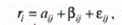
где r_i — доходность ценной бумаги i за данный период; r_j — доходность на рыночный индекс j за этот же период; а_ij — коэффициент смещения; β_ij — коэффициент наклона; ε_ij — случайная погрешность.

Как следует из уравнения представленного ранее, чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги, ε_ij = 0. Разность между действительным и ожидаемым значениями объясняется случайной погрешностью. Поэтому лишь только в ряде маловероятных случаев ε_ij = 0. Это объясняет тот факт, что ценная бумага лежит на линии.

Случайная погрешность позволяет сделать и другое предположение, что при данной доходности на рыночный индекс действительная доходность ценной бумаги обычно лежит вне прямой, задаваемой уравнением рыночной модели. При этом случайная погрешность, будучи случайной переменной с нулевым математическим ожиданием, всегда имеет стандартное отклонение относительно индекса рынка J.

Наклон линии в рыночной модели ценной бумаги определяется чувствительностью ее к доходности на рыночный индекс. Коэффициент наклона в рыночной модели называют «бета»-коэффициентом, который рассчитывается по формуле:

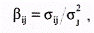
где σ_ij — ковариация между доходностью акции i и доходностью акции рыночного индекса; σ_j —дисперсия доходности индекса или риск ценной бумаги.

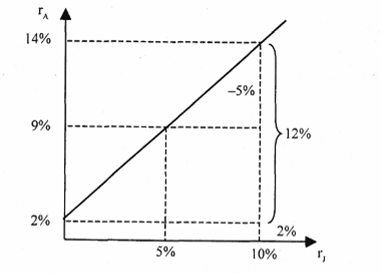
Рис. 1 Зависимость доходности ценной бумаги А от доходности на рыночный индекс

Если ценные бумаги имеют «бета»-коэффициент больше единицы, т.е. обладают большей изменчивостью, чем рыночный индекс, то их называют «агрессивными». И наоборот, ценные бумаги с коэффициентом меньше 1 называют «оборонительными».

Общий риск ценной бумаги (σ_J), измеряемый ее дисперсией (σ_J²), состоит из двух частей: рыночного (или систематического) риска и собственного (или несистематического) риска. Таким образом, σ_J² можно выразить:

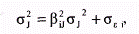
где σ_J² — дисперсия доходности рыночного индекса; β²_ijσ_J² — рыночный риск i ценной бумаги; σ_ε — собственный риск i ценной бумаги, мерой ε которого является дисперсия случайной погрешности (ε_ij).

Зная о весе и рыночном индексе каждой дисконтированной ценной бумаги в портфеле, а также о долях инвестирования в каждую бумагу, доходность портфеля можно рассчитать по формуле:

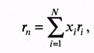
где х_i = 1, 2, 3,..., N.

Подставив значение r_i в указанное уравнение, получим:

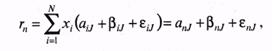
где

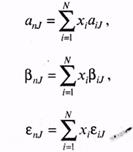
Из 3-х уравнений видно, что в качестве весов выступает доля каждого типа ценных бумаг в портфеле.

Общий риск портфеля, измеряемый дисперсией его доходности, можно определить по формуле:

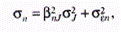
где

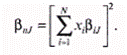
Если же предположить, что случайные отклонения доходности ценных бумаг являются некоррелируемыми, т.е. несвязанными между собой, то получим:

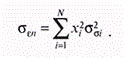
Таким образом, общий риск портфеля состоит из общего риска отдельных ценных бумаг, включающего в себя собственный риск (σ²_εn), которого, по утверждению Г. Марковица, нельзя избежать, и рыночный риск:

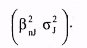
Собственный риск портфеля, или несистематический риск, связан с тем, что находящиеся в портфеле некоторые ценные бумаги могут как возрасти в цене, так и упасть. Следовательно, практически в любом портфеле будут иметь место ценные бумаги, которые могут одинаково влиять на его доходность. Сделав это предположение, можно показать, что если рассмотреть портфель ценных бумаг, в каждую из которых вложено одинаковое количество средств, то доля х составит 1/N, а уровень собственного риска соответственно будет равен:

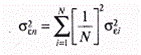
или

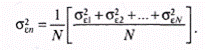
Понятно, что значение, находящееся внутри квадратных скобок в указанном уравнении, является средним собственным риском ценных бумаг, входящих в портфель. Если же увеличить число ценных бумаг (N), то сократится риск сформированного портфеля. На рис. 2 показана зависимость риска от диверсификации портфеля. Существует и другое положительное свойство диверсификации портфеля: оно приводит к усреднению рыночного риска путем изменения «бета»-коэффициента в зависимости от числа ценных бумаг, входящих в портфель.

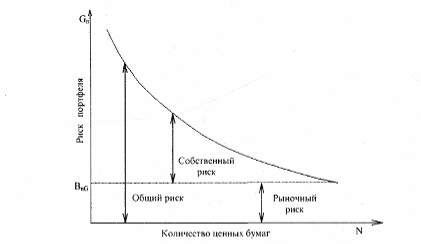
Рис. 2 Зависимость риска от диверсификации портфеля

Подход, использующий рыночную модель, является приблизительным, как впрочем и все рассматриваемые в данном параграфе подходы.

С помощью предложенного Г.Марковицем метода можно сформировать большое количество портфелей ценных бумаг, часть из которых будет относиться к эффективному множеству. Для выделения оптимальных портфелей, т.е. набора относительных долей акций и облигаций, которые могут принести их владельцу максимальный доход, Г.Марковиц использовал алгоритм квадратического программирования (метод критических линий).

Нахождение оптимального портфеля с помощью указанного алгоритма включает в себя ряд процедур:

· рассмотрение портфелей, доступных инвестору;

· нахождение структуры ценных бумаг каждого из бесконечного множества портфелей;

· оценку вектора ожидаемых доходностей и ковариационной матрицы;

· определение количества «угловых» портфелей. Под «угловым» портфелем понимается портфель, обладающий такими свойствами, что любая комбинация двух смежных «угловых» портфелей представляет из себя третий гюруфель, лежащий в эффективном множестве между этими двумя «угловыми» портфелями;

· выбор оптимального портфеля.

Процедура определения состава оптимального портфеля осуществляется с помощью графического нахождения инвестором уровня его доходности. По сути, если нанести на кривые безразличия, то можно найти такую точку О*, в которой доходность портфеля будет максимальна (рис. 3). Для этого следует нанести с помощью компьютера перпендикулярную к оси _р линию, а затем определить два «угловых» портфеля с ожидаемыми доходностями, находящихся в окрестности эффективного множества.

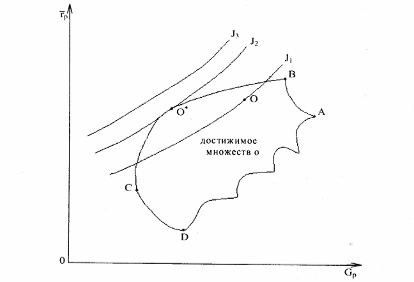
Рис. 3 Нахождение состава оптимального портфеля

Ближайший «угловой» портфель будет расположен выше точки О, что соответствует большей ожидаемой доходности и ниже углового портфеля с соответственно меньшей ожидаемой доходностью.

Если ожидаемую доходность оптимального портфеля обозначим как r* и ожидаемые доходности двух ближайших «угловых» портфелей обозначим как r^a и r^b соответственно, то состав оптимального портфеля может быть рассчитан по следующей формуле:

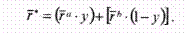
Оптимальный портфель будет состоять из доли у, инвестированной в ближайший «угловой» портфель, находящийся выше оптимального, и доли, равной 1 - у, инвестированной в ближайший угловой портфель, расположенный ниже оптимального.

Таким образом, предложенный выше Г. Марковицемподход ориентирован на то, что инвестор имеет некоторый начальный капитал, что позволяет ему полностью использовать его для формирования портфелей с определенным риском. При этом оптимальный портфель идентифицируется точкой касания кривых безразличия инвестора с эффективным множеством, характеризуемым не только определенной доходностью, но и риском.

Рассмотрим ряд подходов к определению оптимальных портфелей ценных бумаг.

Большой вклад в решение этой проблемы внесли Джеймс Тобин и Уильям Шарп. Они развили подход Марковица в ситуации, когда в экономике существует безрисковый актив с некоторой доходностью.

Под безрисковым активом понимается актив, доходность от которого является определенной. И поскольку неопределенность конечной стоимости безрискового актива отсутствует, то, соответственно, стандартное отклонение для безрискового актива равно нулю.

Если безрисковый актив имеет заранее известную доходность, то некие ценные бумаги, входящие в актив, должны обеспечивать инвестору фиксированный доход. В этой связи вряд ли корпоративные ценные бумаги могут принести инвестору фиксированный доход. В России, по-видимому, только один тип ценных бумаг можно было до недавнего времени отнести к безрисковым — это облигации федерального сберегательного займа.

Инвестирование в безрисковый актив иногда называют безрисковым кредитованием.

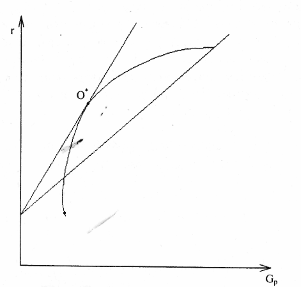
Рис. 3 CML

Дж. Тобин показал, что если р = (р_i, ...р_п) — некоторый портфель (р_i— для i-го актива в портфеле), а f— безрисковый актив, то все портфели вида:

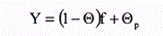
лежат на прямой, проходящей через точки (0, r_f) и (σ_р , _p). Среди всех таких прямых нужно выбрать самую крутую (более крутая дает большую доходность при заданном риске р), т.е. ту, которая проходит через точку (0, r_р ) и точку касания 0* к эффективной границе.

Это новая эффективная граница, полученная с учетом безрискового актива. Ее называют рыночной линией (CML, Capital Market Line), а точку называют рыночным портфелем (market portfolio).

Смысл термина указал Уильям Шарп, который показал, что портфель можно вычислить на основе условия равенства спроса и предложения финансовых активов, рассматривая рынок в полном объеме как совокупность всех инвесторов и всех ценных бумаг (активов). В этом случае доля акций типа i в портфеле 0* просто равна доле всех акций типа i на рынке. Поэтому О* и называют рыночным портфелем.

Алгоритм Марковица-Тобина дает решение задачи составления оптимального портфеля. Но в ситуации, когда нужно исследовать очень большое количество акций, он нереализуем из-за сложности вычислений (нужно обращать матрицу огромного размера).