Определение ошибки выборки для доли фирм со среднесписочной численностью менеджеров 40 человек и более, а также границ, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

,

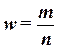где m – число единиц совокупности, обладающих заданным свойством;

n – общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 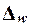доли единиц, обладающих заданным свойством, рассчитывается по формуле

,

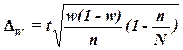где w – доля единиц совокупности, обладающих заданным свойством;

(1-w) – доля единиц совокупности, не обладающих заданным свойством,

N – число единиц в генеральной совокупности,

n– число единиц в выборочной совокупности.

Предельная ошибка выборки 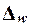определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:

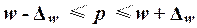
По условию Задания 3 исследуемым свойством фирм является равенство или превышение среднесписочной численности менеджеров величины 40 человек.

Число фирм с данным свойством определяется из табл. 3 (графа 3):

m=7

Рассчитаем выборочную долю:

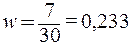
Рассчитаем предельную ошибку выборки для доли:

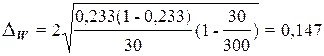
Определим доверительный интервал генеральной доли:

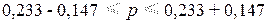
0,086 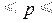0,380

или

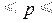8,6% 38%

Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности фирм региона доля фирм со среднесписочной численностью менеджеров 40 человек и более будет находиться в пределах от 8,6% до 38%.

Литература

1. Громыко Г.Л. Теория статистики: Учебник. - М.: ИНФРА-М, 2006.

2. Громыко Г.Л. Теория статистики: Практикум. - М.: ИНФРА-М, 2003.

3. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М.: ЮНИТИ - ДАНА, 2001.

4. Гусаров В.М. Статистика: Учеб пособие/ В.М. Гусаров, Е.И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.

5. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под. ред. Башиной О.Э., Спирина А.А. – М.: Финансы и статисика, 2005.

6. Практикум по статистике: Учеб. пособие для вузов/ Под ред. В.М. Симчеры. - М.: Финстатинформ, 1999.

7. Практикум по теории статистики: Учебное пособие/Под. ред. Шмойловой Р.А. – М.: Финансы и статистика, 2004.

8. Сироткина Т.С., Каманина А.М. Основы теории статистики: Учеб. пособие для вузов/ Под ред. проф. В.М. Симчеры. - М.: Финстатинформ, 1995, 1996.

9. Статистика: Учеб. пособие/А.В. Багат, М.М. Конкина, В.М. Симчера и др.; Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005.

10. Теория статистики: Учебник/Под. ред. Шмойловой Р.А. – М.: Финансы и статистика, 2001; 2003; 2006.

Содержание

Введение ………………………………………………………………..

Раздел I Методические рекомендации к выполнению

статистических расчётов…………………………….............................

Задание 1……………………………………………………………………………

Задание 2……………………………………………………………………………

Задание 3……………………………………………………………………………

Раздел IIОбразец выполнения оформления Заданий 1-3

курсовых и контрольных работ………………………………………..

Задание 1……………………………………………………………………………

Задание 2……………………………………………………………………………

Задание 3……………………………………………………………………………

Литература……………………………………………………………...

[1] Если в дискретном ряду все варианты встречаются одинаково часто, то в этом случае мода отсутствует. Могут быть распределения, где не один, а два (или более) варианта имеют наибольшие частоты. Тогда ряд имеет две (или более) моды, распределение является бимодальным (или многомодальным),что указывает на качественную неоднородность совокупности по изучаемому признаку.