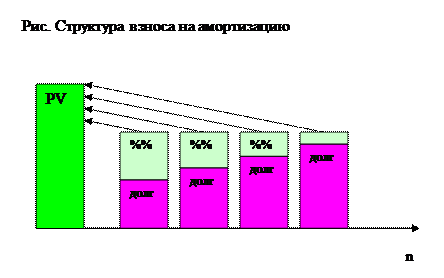
Где on — погашение процентов; of— погашение кредита.

Пример 15. Какова величина ежегодного взноса в погашение кредита $ 15000, предоставленного на 5 лет под 10 % годовых.

РМТ = 3956,96.

Пример 16. У Вас есть долг 1000 ден. Ед. на 5 лет под 10% С долгом Вы рассчитываетесь путем периодических платежей в конце каждого года. Каждый год Вы платите для того, чтобы рассчитаться с долгом и процентами по нему. Условия кредита: обычный вариант, годовые выплаты. Ответ 263,8

Год	Остаток долга на начало года	Сумма%	Остаток долга на конец года	Взнос на амортиз	Погашение основной суммы	Остаток на конец долга
	1000,00	100,00	1100,00	263,80	163,80	836,20
	836,20	83,62	919,82	263,80	180,18	656,02
	656,02	65,60	721,62	263,80	198,20	457,82
	457,82	45,78	503,60	263,80	218,02	239,80
	239,80	23,98	263,78	263,80	239,82	-0,02

Используя аналогичные рассуждения, можно получить величину взноса на амортизацию капитала для авансового аннуитета:

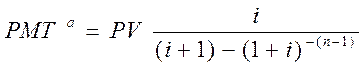
ПРАКТИКУМ

Временная теория денег

Задание №1.

Индейцы продали о. Манхэттен в 1626 году за товары стоимостью $24. Какая сумма накопилась бы на счете сегодня, если бы они вложили эти деньги в банк под 6% годовых. Используйте технику простого и сложного процента.

Задание №2.

Стоимость земли, купленной за $8000 повышается на 15% в год (по сложному проценту). Сколько она будет стоить через 3 года.

Задача №3.

Предприниматель только что заплатил $100 за опцион на покупку земли. Опцион дает ему право приобрести собственность за $10000 по истечении двух лет. Уже выплаченные за опцион $100 не будут включены в цену покупки. Какую сумму сегодня необходимо положить в банк, выплачивающий 10% годовых при ежеполугодовом накоплении с тем, чтобы через два года иметь нужную сумму для приобретения собственности?

Задача №4.

Вкладчик хочет получить $8000, вложив сегодня $1000 под 12% годовых. Сколько полных платежных периодов понадобится для осуществления цели?

Задание №5.

Пенсионный фонд принимает взносы под 10% годовых. Какая сумма будет накоплена к выходу на пенсию, если из зарплаты в конце каждого из 10 лет перечислять в пенсионный фонд $500.

Задача №6.

Каждый месяц вы получаете от квартиры сданной в аренду $50. Эти деньги вы вкладываете в банк под 10% годовых. Сколько денег у вас будет через 5 лет? Задание №7.

Молодая семья планирует купить квартиру через 5 лет. Ее доходы позволяют в начале каждого года вкладывать в банк $1000 под 10% годовых. Сколько денег будет на счете через 5 лет.

Задание №8.

Владелец жилой недвижимости планирует заменить кровлю на своих зданиях через 5 лет. Он полагает, что через 5 лет это ему обойдется в $20000. Какую сумму он должен депонировать по окончании каждого года с учетом того, что средства на счете будут накапливаться по годовой ставке 10%.

Задача №9.

Через 5 лет понадобится $20000. Какую сумму депонировать в начале каждого года на счет в банк, начисляющий 10% годовых?

Задание №10.

Сколько надо положить на счет в банк под 10% годовых, чтобы через 10 лет купить квартиру за $30000.

Задача №11.

Через 7 лет необходимо иметь $3000. Достаточно ли положить в банк $1200, если он начисляет процент ежеквартально, годовая ставка равна 10%.

Задание №12.

Земельный спекулянт рассчитывает, что через 2 года массив площадью 10 га может быть продан за $1000 за га. Какая сегодняшняя цена позволит спекулянту получить 15% годовой доход.

Задача №13.

Определить сумму сегодняшних инвестиций, дающих право ежегодного получения $100 дохода в конце каждого года на протяжении 4 лет при ставке дисконта 10%. Сделать проверку, используя "метод депозитной книжки".

Задача №14.

Какова текущая стоимость ипотечного кредита, предусматривающего выплату $1000 в начале каждого года в течение 15 лет. Ставка дисконта 10%.

Задание №15.

Аренда магазина принесет его вкладчику в течение первых трех лет ежегодный доход $3000, в последующие 5 лет доход составит $4500. Определить текущую стоимость совокупного дохода, если ставка дисконта 10%.

Задание №16.

Какую сумму целесообразно заплатить инвестору за объект недвижимости, который можно эффективно эксплуатировать в течение 5 лет. Объект в конце каждого года приносит доход по 350000 руб. Требуемый доход на инвестиции — 20%. Проверить методом "депозитной книжки".

Задание №17.

Рассчитать величину ежегодного взноса в погашение кредита в сумме $15000, предоставленного на 5 лет под 10% годовых.

Задание №18.

Банк предоставляет кредит $10000. Его нужно погашать в конце каждого полугодия в течение 2 лет. Кредит предоставлен под 10% годовых. Каким будет каждый полугодовой платеж.

Задание №19.

Какое вложение денег является наиболее выгодным:

a) приобретение права аренды магазина за $30000 на 7 лет, магазин приносит ежегодно $8000 чистого операционного дохода;

b) вложить $30000 в банк под 10% годовых.

Задание №20.

Строительная фирма предлагает вам квартиру на таких условиях. Вы в течение 25 лет ежегодно выплачиваете $4000 при ставке ипотеки 10%. Оценщик оценил вашу квартиру в $30000. Согласитесь ли вы на этот контракт.

Задание №21.

Отдельно стоящий магазин для розничной торговли сдан в аренду на 25 лет за $5000 в год, вносимых в конце каждого года. У арендатора есть опцион на покупку здания по истечении срока аренды за $65000. В этом случае инвесторы стремятся к получению 10%-ного дохода на инвестиции. Какова текущая стоимость объекта.

Задание №22.

Вы выиграли конкурс. По его условиям вы можете получить $1000 сейчас наличными или $2000 — через 5 лет. Какой приз вы выберете, если банк принимает вклады под 10% годовых?

Ипотечное кредитование

Задание №1.

Однокомнатная квартира стоит $9000 в наличии имеется $2000. Недостающую сумму решено взять в банке под 20% годовых на 5 лет. Составить схему погашения ипотечного кредита.

Задание №2.

Кредит в размере $1000 выдан на 4 года под 12% годовых. Возмещение основной суммы кредита происходит ежегодно равными частями. Построить схему погашения кредита.

Задание №3.

Начальная сумма кредита $30000, срок кредита 5 лет, начальная норма процента - 10%. Начальная норма будет скорректирована в сторону увеличения на 1% в конце 1 года и еще на 2% в конце второго года, далее не изменится. Построить схему погашения кредита.

Задание №4.

Сумма кредита равна $25000, номинальная ставка определена в 10%, ежегодный платеж должен составлять $2651,98. Какое время потребуется для полной амортизации кредита. Постройте таблицу погашения кредита на первые 3 года.

Задание №5.

Стоимость объекта недвижимости $250000. Коэффициент ипотечной задолженности — 40%. Кредит предоставлен на 5 лет под 5% годовых и предусматривает периодическую выплату только процентов. Однако через 5 лет должна быть единовременно погашена вся основная сумма кредита. Заемщик хочет в конце каждого года вносить в банк определенную сумму с тем, чтобы иметь возможность выплачивать проценты по кредиту и погасить долг через 5 лет. Банк начисляет ежегодно 10% годовых. Какую сумму необходимо вносить в банк для погашения кредита.

Задача №6.

Ипотечный кредит на сумму $50000 выдан на 15 лет при 10% годовых и ежегодных платежах. За досрочное погашение кредита предусмотрен штраф в размере 8% от невыплаченной суммы кредита. Определить действительную норму процента по кредиту при условии его досрочного погашения в конце 3 года.

Задача №7.

Господин Иванов купил квартиру стоимостью $20000 с привлечением ипотечного кредита. При оформлении сделки он заплатил фирме $3000, а остальные обязался выплатить в течение года под 35% в год. Определите сумму ежемесячных платежей по кредиту.