Модель оценки стоимости активов (CAPM)
Финансовая теория гласит, что более рискованные активы должны предлагать более высокую ожидаемую доходность, и модели ценообразования активов это учитывают. В условиях хорошо развитого рынка информация быстро находит отражение на динамике курса ценных бумаг.
В середине 60-х годов XX века У.Шарпом и ДжЛинтерном была разработана модель, описывающая взаимосвязь между риском и ожидаемой доходностью актива. Она получила название модели оценки стоимости активов (Capital Asset Pricing Model, CAPM).
CAPM и исходит из того, что акции тем рискованнее, чем больше динамика их курса увязана с динамикой курсов на рынке в целом. CAPM является моделью одного временного периода.
Модель CAPM строится на основе нескольких предположений:
1. Оценка инвестиционных портфелей производится на основе ожидаемой доходности и стандартного отклонения.
2. Выбирая из двух портфелей, предпочтение отдается портфелю с наибольшей ожидаемой доходностью, при прочих равных условиях.
3. Выбирая из двух портфелей, предпочтение отдается портфелю с наименьшим стандартным отклонением, при прочих равных условиях.
4. При желании инвестор может купить часть акции, т.е. активы делимы.
5. Существует безрисковая процентная ставка, одинаковая для всех инвесторов, по которой можно получить кредит или дать в долг.
6. Налоги и операционные издержки несущественны.
7. Период инвестирования для всех инвесторов одинаков.
8. Информация свободна и незамедлительно получается всеми инвесторами.
9. Инвесторы имеют однородные ожидания, т.е. одинаково оценивают ожидаемую доходность, стандартное отклонение и ковариации доходностей ценных бумаг.
Зависимость между риском и ожидаемой доходностью графически описывается с помощью линии рынка капитала (Capital Market Line, CML).
 |
| где |  – рыночный портфель; – рыночный портфель; |
 – безрисковая ставка доходности; – безрисковая ставка доходности; | |
 – линия рынка капитала (CML); – линия рынка капитала (CML); | |
 – ожидаемый риск рыночного портфеля; – ожидаемый риск рыночного портфеля; | |
 – ожидаемая доходность рыночного портфеля. – ожидаемая доходность рыночного портфеля. |
Эффективные портфели находятся вдоль прямой  , имеющей название линии рынка капитала (CML), и образуются различными комбинациями риска и доходности, получаемыми в сочетании рыночного портфеля с безрисковым заимствованием или кредитованием. Все остальные портфели, не использующие комбинации рыночного портфеля и безрискового заимствования или кредитования, будут лежать ниже CML.
, имеющей название линии рынка капитала (CML), и образуются различными комбинациями риска и доходности, получаемыми в сочетании рыночного портфеля с безрисковым заимствованием или кредитованием. Все остальные портфели, не использующие комбинации рыночного портфеля и безрискового заимствования или кредитования, будут лежать ниже CML.
Уравнение CML имеет следующий вид:

CML описывает соотношение риска и ожидаемой доходности только для широко диверсифицированных (эффективных) портфелей, но не отвечает на вопрос, какой ожидаемой доходностью должны обладать менее диверсифицированные портфели или отдельные активы.
На этот вопрос отвечает линия рынка актива (Security Market Line, SML).
 |
SML проходит через точку М, отображающую рыночный портфель. Значение β для этой точки равно 1, а ожидаемая доходность равна  . Так как значение беты для безрисковых бумаг равно 0, то SML должна проходить также через точку с координатами 0 и
. Так как значение беты для безрисковых бумаг равно 0, то SML должна проходить также через точку с координатами 0 и  .
.
Ожидаемая премия за риск инвестиций, бета которых равна 0,5, составляет половину ожидаемой премии за рыночный риск. Ожидаемая премия за риск инвестиций с бетой, равной 2,0, в два разапревышает ожидаемую премию за рыночный риск.
Ожидаемую доходность акций, превышающую безрисковую ставку  , или «ожидаемую избыточную доходность», можно выразить следующим образом:
, или «ожидаемую избыточную доходность», можно выразить следующим образом:

Инвестор всегда может получить ожидаемую премию за риск  , комбинируя рыночный портфель и безрисковые займы. Так, на хорошо функционирующем рынке никто не держит акции, предлагающие премию за ожидаемый риск, меньше,чем
, комбинируя рыночный портфель и безрисковые займы. Так, на хорошо функционирующем рынке никто не держит акции, предлагающие премию за ожидаемый риск, меньше,чем  .
.
Угол наклона SML определяется отношением инвесторов к риску в условиях рынка, т.е. коэффициентом β (или коэффициентом наклона рыночной модели). Чем выше риск, тем более крутой наклон будет у SML.
Существуют ли какие-либо акции, лежащие выше линии рынка ценных бумаг? Если мы возьмем все акции в совокупности, мы получим рыночный портфель. Следовательно, мы знаем, что акции в среднемрасполагаются на линии. Так как ни одна не лежит нижелинии, то ни одна не может лежать и выше линии. Таким образом, любая акция должна лежать на линии рынка актива и обеспечивать премию за ожидаемый риск.
Так как ожидаемая доходность портфеля равна средневзвешенной доходностей активов, входящих в портфель, то каждый актив, а соответственно и портфель, будет лежать на SML. Следовательно, эффективные портфели лежат как на CML, так и на SML. Неэффективные портфели также лежат на SML, но ниже CML.
Константа пропорциональности  – это ожидаемая избыточная доходность по рынку в целом. Часто ее называют премией к цене акций. Отсюда, ожидаемая доходность актива, определяемая с помощью уравнения SML, равна:
– это ожидаемая избыточная доходность по рынку в целом. Часто ее называют премией к цене акций. Отсюда, ожидаемая доходность актива, определяемая с помощью уравнения SML, равна:

Пример: Предположим, что ожидаемая рыночная доходность равна 15%, безрисковая ставка равна 7%. Если «бета» акции равна 1,3, то какова ее ожидаемая доходность в соответствии с CAPM?
Решение:  = 17,4%
= 17,4%
Оценка эффективности управления портфелем
Оценка результативности управления портфелем включает в себя определение фактической доходности и риска портфеля за рассматриваемый период, и эталонного портфеля, который используется в качестве точки отсчета для сравнительного анализа.
На практике приходится сравнивать результаты управления портфелем различных менеджеров. Если сравнивать портфели только на основе их абсолютных значений, то, как правило, сложно сделать правильную оценку. Например, доходность одного портфеля за год составила 150%, а второго – 100%. Результаты управления первым портфелем кажутся более предпочтительными. Однако, если его риск был в два раза больше риска второго портфеля, то более успешным оказался второй менеджер.
Поэтому для оценки эффективности управления портфелем используют относительные показатели, которые учитывают как доходность, так и риск портфеля.
Первый показатель называют коэффициентом Шарпа:

| где | rр – средняя доходность портфеля за период; |
 – безрисковая ставка доходности; – безрисковая ставка доходности; | |
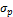 – ожидаемый риск портфеля; – ожидаемый риск портфеля; |
Коэффициент Шарпа учитывает доходность портфеля, полученную сверх ставки без риска, и весь риск, как рыночный, так и нерыночный.
Второй показатель – это коэффициент Трейнора. В качестве меры риска здесь учитывается бета портфеля.

Показатель Шарпа в качестве риска учитывает стандартное отклонение, и поэтому его следует использовать инвестору, портфель которого не является широко диверсифицированным. Показатель Трейнора лучше подходит для диверсифицированного портфеля. Чем выше значения коэффициентов, тем лучше результаты управления.
