Приведите классификацию криптографических алгоритмов и охарактеризуйте их. Раскройте алгоритм шифрования RSA.

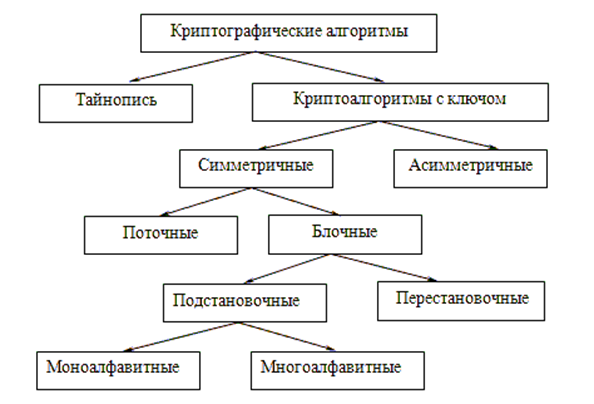
Тайнопись предполагает, что отправитель и получатель производят над сообщением преобразования, известные только им двоим.

В противовес тайнописи, криптоалгоритмы с ключом построены на том принципе, что алгоритм воздействия на передаваемые данные известен всем сторонним лицам, но он зависит от некоторого параметра, который держится в секрете – «ключа», который известен только двум лицам, участвующим в обмене информацией.

Отличительной чертой симметричных алгоритмов шифрования является наличие одного ключа шифрования, который должен быть известен только отправителю и получателю сообщения.

Отличительной особенностью асимметричных алгоритмов является наличие пары ключей шифрования: открытого k_от, который передается второй стороне по незащищенному каналу связи и поэтому может быть известен криптоаналитику, а также закрытого k_зак, который известен лишь одному человеку (получателю сообщения) и держится в секрете

В зависимости от размера блока шифруемой информации криптоалгоритмы делятся на блочные и поточные шифры. Единицей кодирования в потоковых шифрах является один бит. Результат кодирования не зависит от прошедшего ранее входного потока. Для блочных шифров единицей кодирования является блок из нескольких байтов. Результат кодирования зависит от всех исходных байтов этого блока.

Еще одним критерием классификации криптоалгоритмов является тип выполняемых преобразований над блоками открытого текста. В перестановочных шифрах блоки информации не изменяются сами по себе, но изменяется их порядок следования, что делает информацию недоступной стороннему наблюдателю. Подстановочные шифры изменяют сами блоки информации по определенным законам.

Деление криптоалгоритмов на моноалфавитные и многоалфавитные характерно для подстановочных шифров. Моноалфавитные криптоалгоритмы заменяют блок входного текста (символ входного алфавита) на один и тот же блок шифротекста (символ выходного алфавита). В многоалфавитных шифрах одному и тому же блоку входного текста могут соответствовать разные блоки шифротекста, что существенно затрудняет криптоанализ.

Система RSA построена с использованием степенной односторонней функции с секретом f(x)=xеmodn. Блок x открытого текста, представленный как целое число из сегмента [0,n-1], преобразуется в блок у шифртекста из того же сегмента:

у=Е(е,п)(х)=xе modn,

где (е,п) – открытый ключ зашифрования. При расшифровании блок х открытого текста вычисляется также с помощью степенной функции, но с другим показателем d, являющимся закрытым ключом:

x=D(d,п)(y)=yd modn.

В основе согласованности этих преобразований лежит теорема Эйлера, в соответствии с которой для каждого числа x, взаимно простого с модулем п, выполнено сравнение:

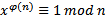
где 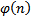– функция Эйлера (число натуральных чисел, не превосходящих п и взаимно простых с п), вычисляемая по формуле

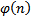=п (1-1/р1) … (1-1/Ps),

если каноническое разложение числа п есть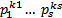

Чтобы воспользоваться теоремой Эйлера, в криптосистеме RSA используют числа е и d, связанные соотношением:

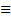ed 1 mod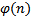

Определим правила, по которым надо выбирать числа е, d и п. Вообще, зная 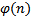, число е можно выбрать взаимно простым с 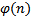, проверив свойство (е 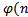))=1 с помощью алгоритма Евклида. Тогда d есть решение сравнения (1), и расширенный алгоритм Евклида позволяет определить числа d и v такие, что еd+v 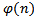=1. В качестве е можно взять простое число из множества {3,…, }.

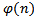В системе RSA модуль п=рq - произведение двух секретных простых чисел р и q, поэтому 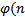)=(р-1)(q-1). Если взять простое число е и при этом е>max(р,q), то (е, 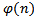)=1, т.е. при выработке такого ключа е можно воспользоваться быстрыми тестами проверки чисел на простоту и не применять алгоритм Евклида.

Без знания простых сомножителей р и q трудно определить значение 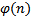, и значит, при секретном числе d определение открытого текста по шифрованному сводится для криптоаналитика либо к трудной задаче извлечения корня степени е из числа y по модулю п, либо к трудной задаче разложения числа п на простые множители.