Модель оценки финансовых активов

Предположения

Для того чтобы понять, как складываются цены финансовых активов, необходимо скон­струировать модель. Это требует упрощений, позволяющих создателю модели абстрагироваться от всей сложности ситуации и рас­сматривать только наиболее важные ее элементы. С этой целью формулируются опре­деленные предположения об объекте исследования. Эти упрощающие предположения призваны обеспечить степень абстракции, позволяющую построить модель.

Это следующие предположения:

1. Инвесторы производят оценку инвестиционных портфелей, основываясь на ожи­даемых доходностях и их стандартных отклонениях за период владения.

2. Инвесторы никогда не бывают пресыщенными. При выборе между двумя портфе­лями они предпочтут тот, который, при прочих равных условиях, дает наиболь­шую ожидаемую доходность.

3. Инвесторы не желают рисковать. При выборе между двумя портфелями они предпочтут тот, который, при прочих равных условиях, имеет наименьшее стан­дартное отклонение.

4. Частные активы бесконечно делимы. При желании инвестор может купить часть акции.

5. Существует безрисковая процентная ставка, по которой инвестор может дать взаймы (т.е. инвестировать) или взять в долг денежные средства.

6. Налоги и операционные издержки несущественны.

Эти предположения дополняются следующими:

7. Для всех инвесторов период вложения одинаков.

8. Безрисковая процентная ставка одинакова для всех инвесторов.

9. Информация свободно и незамедлительно доступна для всех инвесторов.

10. Инвесторы имеютоднородные ожидания, т.е. они оди­наково оценивают ожидаемые доходности, среднеквадратичные отклонения и ковариации доходностей ценных бумаг.

Как вытекает из этих предположений, в САРМ рассматривается предельный слу­чай. Все инвесторы обладают одной и той же информацией и по-одинаковому оцени­вают перспективы ценных бумаг. Неявно это означает, что они одинаковым образом анализируют получаемую информацию. Рынки ценных бумаг являютсясовершеннымирынками в том смысле, что в них нет факторов, которые бы препятст­вовали инвестициям. Такие потенциальные препятствия, как ограниченная делимость, налоги, операционные издержки, и различие между ставками безрискового заимство­вания и кредитования считаются отсутствующими. Это позволяет сместить фокус рас­смотрения с того, как следует инвестору размещать свои средства, на то, что произойдет с курсами ценных бумаг, если все инвесторы будут поступать одинаково. Исследуя коллективное поведение всех инвесторов на рынке, можно выявить характер конечной равновесной зависимости между риском и доходностью каждой ценной бумаги.

Уравнение модели САРМ

В модели САРМ простым образом определяется связь между риском и доходностью эффективных портфелей. Это наглядно представлено на рисунке ниже:

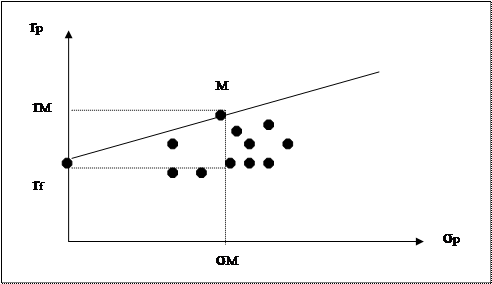Точка М обозначает рыночный портфель, а rf представляет собой безрисковую ставку доходности. Эффективные портфели находятся вдоль прямой, пересекающей ось ординат в точке с коорди­натами (0, r) и проходящей через М, и образуются альтернативными комбинациями риска и доходности, получаемыми в результате сочетания рыночного портфеля с безрис­ковым заимствованием или кредитованием. Это линейное эффективное множество в САРМ известно под названиемрыночная линия (Capital Market Line, CML). Все осталь­ные портфели, не использующие рыночный портфель в комбинации с безрисковым заимствованием или кредитованием, будут лежать ниже рыночной прямой, хотя неко­торые могут располагаться в непосредственной близости от нее.

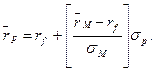Наклон СМL равен разнице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги, деленной на разницу их рисков. Так как СМL пересекает вертикальную ось в точке с координа­тами (0, r), то уравнение СМL имеет вид:

Состояние равновесия на рынке ценных бумаг может быть охарактеризовано дву­мя ключевыми величинами. Первая - это ордината точки пересечения СМL с верти­кальной осью (т.е. безрисковая ставка), которую часто называют наградой за ожидание. Вторая — это наклон СМL, который называют наградой за единицу принятого риска.