Лекция 5. формирование и управление инвестиционным портфелем

ЛЕКЦИЯ 5. ФОРМИРОВАНИЕ И УПРАВЛЕНИЕ ИНВЕСТИЦИОННЫМ ПОРТФЕЛЕМ

ОГЛАВЛЕНИЕ

ПОНЯТИЕ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ И ПРИНЦИПЫ ЕГО ФОРМИРОВАНИЯ 2

Типы портфелей.................................................................................................................... 2

Управление портфелем ценных бумаг............................................................................... 3

Проблема выбора инвестиционного портфеля................................................................. 5

Определение уровня доходности портфеля....................................................................... 6

Кривые безразличия............................................................................................................. 7

Ненасыщаемость и избегание риска................................................................................. 8

Вычисление ожидаемых доходностей и стандартных отклонений портфелей........... 9

ПОРТФЕЛЬНЫЙ АНАЛИЗ................................................................................................ 10

Теорема об эффективном множестве............................................................................... 10

Достижимое множество............................................................................................................................................. 10

Теорема об эффективном множестве в применении к достижимому множеству...................................... 11

Выбор оптимального портфеля............................................................................................................................... 11

Выпуклость эффективного множества.................................................................................................................. 12

Рыночная модель................................................................................................................ 14

«Бета»-коэффициент................................................................................................................................................... 15

Диверсификация................................................................................................................. 15

МОДЕЛЬ ОЦЕНКИ ФИНАНСОВЫХ АКТИВОВ.......................................................... 16

Предположения................................................................................................................... 16

Уравнение модели САРМ.................................................................................................. 17

ИСТОЧНИКИ........................................................................................................................ 17

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ....................................................................... 18

ПОНЯТИЕ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ И ПРИНЦИПЫ ЕГО ФОРМИРОВАНИЯ

Типы портфелей

В сложившейся мировой практике фондового рынка под инвестиционным портфелем понимается некая совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, выступающая как целостный объект управления.

Смысл портфеля — улучшить условия инвестирования, придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятой ценной бумаги и возможны только при их комбинации.

Таким образом, в процессе формирования портфеля достигается новое инвестиционное качество с заданными характеристиками. Портфель ценных бумаг является инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске.

С учетом инвестиционных качеств ценных бумаг можно сформировать различные портфели ценных бумаг, в каждом из которых будет собственный баланс между существующим риском, приемлемым для владельца портфеля, и ожидаемой им отдачей (доходы) в определенный период времени. Соотношение этих факторов и позволяет определить тип портфеля ценных бумаг.

Портфель роста формируется из акций компаний, курсовая стоимость которых растет. Цель данного типа портфеля — рост капитальной стоимости портфеля вместе с получением дивидендов. Однако дивидендные выплаты производятся в небольшом размере. Темпы роста курсовой стоимости совокупности акций, входящих в портфель, определяют виды портфелей, составляющие данную группу.

Портфель агрессивного роста нацелен на максимальный прирост капитала. В состав данного типа портфеля входят акции молодых, быстрорастущих компаний. Инвестиции в портфеле являются достаточно рискованными, но вместе с тем могут приносить самый высокий доход.

Портфель консервативного роста является наименее рискованным. Он состоит в основном из акций крупных, хорошо известных компаний, характеризующихся хотя и невысокими, но устойчивыми темпами роста курсовой стоимости. Состав портфеля остается стабильным в течение длительного периода времени. Инвестиции портфеля консервативного роста нацелены на сохранение капитала.

Портфель среднего роста представляет собой сочетание инвестиционных свойств портфелей агрессивного и консервативного роста. В данный тип портфеля включаются наряду с надежными ценными бумагами, приобретаемыми на длительный срок, рискованные фондовые инструменты, состав которых периодически обновляется. При этом гарантируется средний прирост капитала и умеренная степень риска вложений. Надежность обеспечивается ценными бумагами консервативного роста, а доходность — ценными бумагами агрессивного роста. Портфель среднего роста является наиболее распространенной моделью портфеля и пользуется большой популярностью у инвесторов, не склонных к высокому риску.

Портфель дохода ориентирован на получение высокого текущего дохода — процентных и дивидендных выплат. Портфель дохода составляется в основном из акций дохода, т. е. таких акций, которые характеризуются умеренным ростом курсовой стоимости и высокими дивидендами, облигаций и других ценных бумаг, инвестиционным свойством которых являются высокие текущие выплаты. Особенность этого типа портфеля в том, что цель его создания — получение определенного уровня дохода, величина которого соответствовала бы минимальной степени риска, приемлемого консервативным инвестором. Поэтому объектами портфельного инвестирования являются высоконадежные инструменты фондового рынка, у которых высокое соотношение стабильно выплачиваемого процента и курсовой стоимости.

Портфель регулярного дохода формируется из высоконадежных ценных бумаг и приносит средний доход при минимальном уровне риска.

Портфель доходных бумаг состоит из высокодоходных облигаций корпораций, ценных бумаг, приносящих высокий доход при среднем уровне риска.

Портфель роста и дохода формируется для избежания возможных потерь на фондовом рынке как от падения курсовой стоимости, так и низких дивидендных или процентных выплат. Одна часть финансовых активов, входящих в состав данного портфеля, приносит владельцу рост капитальной стоимости, а другая — доход. Потеря одной части может компенсироваться возрастанием другой.

Охарактеризуем виды портфеля роста и дохода.

• Портфель двойного назначения состоит из бумаг, приносящих его владельцу высокий доход при росте вложенного капитала. В данном случае речь идет о ценных бумагах инвестиционных фондов двойного назначения. Они выпускают собственные акции двух типов, первые — приносят высокий доход, вторые — прирост капитала. Инвестиционные характеристики портфеля определяются значительным содержанием данных бумаг в портфеле.

• Сбалансированные портфели предполагают сбалансированность не только доходов, но и риска, который сопровождает операции с ценными бумагами. Сбалансированные портфели в определенной пропорции состоят из ценных бумаг, быстро растущих в курсовой стоимости, и из высокодоходных ценных бумаг. В состав портфелей могут включаться и высокорискованные ценные бумаги, но, как правило, они формируются из обыкновенных и привилегированных акций, а также облигаций. В зависимости от конъюнктуры рынка в те или иные фондовые инструменты, включенные в портфель, вкладывается большая часть средств.

Если рассматривать типы портфелей в зависимости от степени риска, приемлемого для инвестора, то необходимо вспомнить их классификацию, согласно которой они делятся на консервативный, умеренно-агрессивный, агрессивный и нерациональный. Поэтому каждому типу инвестора будет соответствовать и свой тип портфеля ценных бумаг: высоконадежный, но низкодоходный; диверсифицированный; рискованный, но высокодоходный, безсистемный.

Кривые безразличия

Метод, который будет применен для выбора наиболее желательного портфеля, использует так называемые кривые безразличия. Эти кривые отражают отношение инвестора к риску и доходности и, таким образом, могут быть представлены как двухмерный график, где по горизонтальной оси откладывается риск, мерой которого является стандартное отклонение, а по вертикальной оси — вознаграждение, мерой которого является ожидаемая доходность.

Рисунок представляет собой график кривых безразличия гипотетического инвестора. Каждая кривая линия отображает одну кривую безразличия инвестора и представляет все комбинации портфелей, которые обеспечивают заданный уровень желаний инвестора.

Свойства кривых безразличия:

1. Все портфели, лежащие на одной заданной кривой безразличия, являются равноценными для инвестора. Следствием этого свойства является тот факт, что кривые безразличия не могут пересекаться.

2. Инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее.

В заключение следует заметить, что инвестор имеет бесконечное число кривых безразличия. Это просто означает, что, как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними.

ПОРТФЕЛЬНЫЙ АНАЛИЗ

Достижимое множество

Рисунок ниже представляет иллюстрацию местоположения достижимого множества, также известного как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. Это означает, что все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества.

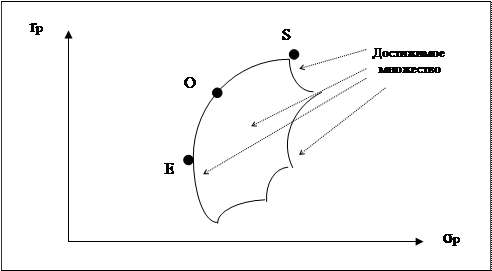Выбор оптимального портфеля

Для выбора оптимального портфеля инвестор должен нарисовать свои кривые безразличия на одном рисунке с эффективным множеством, а затем приступить к выбору портфеля, расположенного на кривой безразличия, находящейся выше и левее остальных. Этот портфель будет соответствовать точке, в которой кривая безразличия касается эффективного множества. Как это видно из рисунке ниже, таким портфелем является портфель О. Несомненно, что инвестор предпочел бы портфель, находящийся на более высокой кривой безразличия, но такого достижимого портфеля просто не существует. Желание находиться на какой-то конкретной кривой не может быть реализовано, если данная кривая нигде не пересекает множество достижимости.

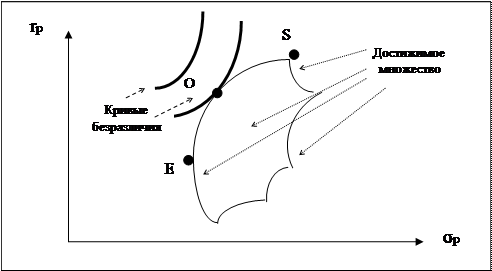Рыночная модель

Предположим, что доходность обыкновенной акции за данный период времени (например, месяц) связана с доходностью за данный период акции на рыночный индекс. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции, а с падением рыночного индекса, вероятно, будет падать и цена акции. Один из путей отражения данной взаимосвязи носит название рыночная модель:

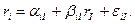где ri, - доходность ценной бумаги i за данный период;

rI - доходность на рыночный индекс I за этот же период;

аiI - коэффициент смещения;

βiI - коэффициент наклона;

ε iI - случайная погрешность.

Предположив, что коэффициент наклона положителен, из уравнения можно заметить следующее: чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги.

«Бета»-коэффициент

Отметим, что наклон в рыночной модели ценной бумаги измеряет чувствительность ее доходности к доходности на рыночный индекс.

Коэффициент наклона рыночной модели часто называют «бета»-коэффициентом и вычисляют так:

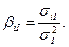где σiI обозначает ковариацию между доходностью акции i и доходностью на рыночный индекс, а σ2I обозначает дисперсию доходности на индекс. Акция, которая имеет доходность, являющуюся зеркальным отражением доходности на индекс, будет иметь «бета»-коэффициент, равный 1. То есть акции с «бета»-коэффициентом больше единицы обладают большей изменчивостью, чем рыночный индекс, и носят название «агрессивные» акции. И наоборот, акции с «бета»-коэффициентом меньше единицы, обладают меньшей изменчивостью, чем рыночный индекс, и называются «оборонительными» акциями.

Диверсификация

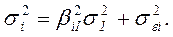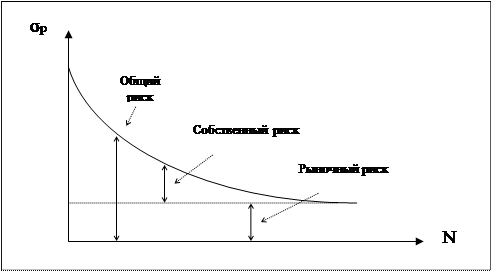
Исходя из рыночной модели, общий риск ценной бумаги i, измеряемый ее дисперсией, состоит из двух частей: (1) рыночный (или систематический) риск, (2) собственный (или несистематический) риск. Таким образом:

Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же.

Предположения

Для того чтобы понять, как складываются цены финансовых активов, необходимо сконструировать модель. Это требует упрощений, позволяющих создателю модели абстрагироваться от всей сложности ситуации и рассматривать только наиболее важные ее элементы. С этой целью формулируются определенные предположения об объекте исследования. Эти упрощающие предположения призваны обеспечить степень абстракции, позволяющую построить модель.

Это следующие предположения:

1. Инвесторы производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и их стандартных отклонениях за период владения.

2. Инвесторы никогда не бывают пресыщенными. При выборе между двумя портфелями они предпочтут тот, который, при прочих равных условиях, дает наибольшую ожидаемую доходность.

3. Инвесторы не желают рисковать. При выборе между двумя портфелями они предпочтут тот, который, при прочих равных условиях, имеет наименьшее стандартное отклонение.

4. Частные активы бесконечно делимы. При желании инвестор может купить часть акции.

5. Существует безрисковая процентная ставка, по которой инвестор может дать взаймы (т.е. инвестировать) или взять в долг денежные средства.

6. Налоги и операционные издержки несущественны.

Эти предположения дополняются следующими:

7. Для всех инвесторов период вложения одинаков.

8. Безрисковая процентная ставка одинакова для всех инвесторов.

9. Информация свободно и незамедлительно доступна для всех инвесторов.

10. Инвесторы имеютоднородные ожидания, т.е. они одинаково оценивают ожидаемые доходности, среднеквадратичные отклонения и ковариации доходностей ценных бумаг.

Как вытекает из этих предположений, в САРМ рассматривается предельный случай. Все инвесторы обладают одной и той же информацией и по-одинаковому оценивают перспективы ценных бумаг. Неявно это означает, что они одинаковым образом анализируют получаемую информацию. Рынки ценных бумаг являютсясовершеннымирынками в том смысле, что в них нет факторов, которые бы препятствовали инвестициям. Такие потенциальные препятствия, как ограниченная делимость, налоги, операционные издержки, и различие между ставками безрискового заимствования и кредитования считаются отсутствующими. Это позволяет сместить фокус рассмотрения с того, как следует инвестору размещать свои средства, на то, что произойдет с курсами ценных бумаг, если все инвесторы будут поступать одинаково. Исследуя коллективное поведение всех инвесторов на рынке, можно выявить характер конечной равновесной зависимости между риском и доходностью каждой ценной бумаги.

Уравнение модели САРМ

В модели САРМ простым образом определяется связь между риском и доходностью эффективных портфелей. Это наглядно представлено на рисунке ниже:

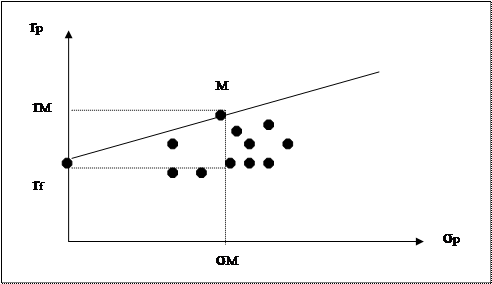Точка М обозначает рыночный портфель, а rf представляет собой безрисковую ставку доходности. Эффективные портфели находятся вдоль прямой, пересекающей ось ординат в точке с координатами (0, r) и проходящей через М, и образуются альтернативными комбинациями риска и доходности, получаемыми в результате сочетания рыночного портфеля с безрисковым заимствованием или кредитованием. Это линейное эффективное множество в САРМ известно под названиемрыночная линия (Capital Market Line, CML). Все остальные портфели, не использующие рыночный портфель в комбинации с безрисковым заимствованием или кредитованием, будут лежать ниже рыночной прямой, хотя некоторые могут располагаться в непосредственной близости от нее.

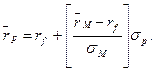Наклон СМL равен разнице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги, деленной на разницу их рисков. Так как СМL пересекает вертикальную ось в точке с координатами (0, r), то уравнение СМL имеет вид:

Состояние равновесия на рынке ценных бумаг может быть охарактеризовано двумя ключевыми величинами. Первая - это ордината точки пересечения СМL с вертикальной осью (т.е. безрисковая ставка), которую часто называют наградой за ожидание. Вторая — это наклон СМL, который называют наградой за единицу принятого риска.