Расчет стоимости и доходности облигаций

Доходность является относительным показателем, характеризующим доход, приходящийся на единицу затрат.

Различают купонную доходность (норма процента, которая указана на ценной бумаге), текущую доходность и полную доходность.

1. Текущая доходность характеризует облигацию как объект долгосрочного инвестирования. Она отражает годовые поступления относительно затрат на приобретения облигации и рассчитывается по формуле.

В расчёте на год:

.

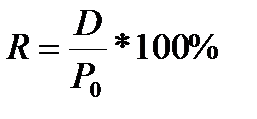В расчёте на другой период:

;

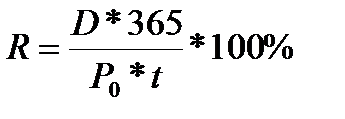где

R – текущая доходность от вложений в облигации, руб.;

D – совокупный купонный доход на 1 облигацию, руб.

P₀ – цена покупки облигации,

t – время в днях, за которое получен купонный доход.

аПример:

Купонный доход по облигации составляет 120 руб., а стоимость ее приобретения составляет 1050 руб. В данном случае текущая доходность составит:

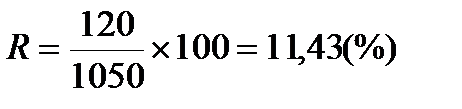
Вместе с тем, текущая доходность не учитывает изменения цены облигации.

2. Показатель полной доходности характеризует полный доход, получаемый от процентных выплат и изменения цены на облигацию, который приходится на единицу затрат по её приобретению.

Если инвестиционный период до 1 года:

;

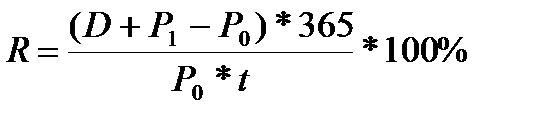где

R – полная доходность от вложений в облигации, руб.;

D – совокупный купонный доход на 1 облигацию, руб.;

P₁ – цена продажи облигации, руб.;

P₀ – цена покупки облигации, руб.;

t – время нахождение облигации у инвестора, дней.

Если инвестиционный период больше года.

Полное число лет:

;

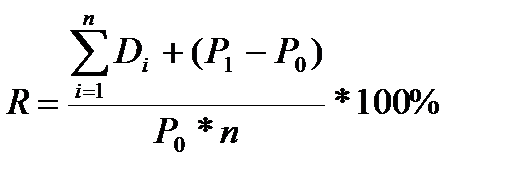где

n – срок вложения (число лет);

D_i – купонный доход за i год, руб.

Неполное число лет:

;

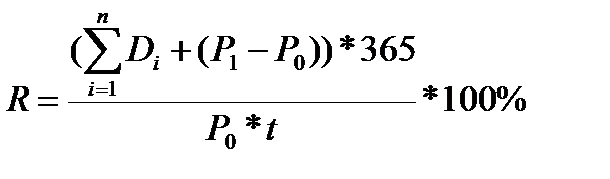где

D_i – купонный доход за i год, руб.;

t – время нахождение облигации у инвестора, дней.

Пример:

Облигация номинальной стоимостью 1000 руб. и купонной ставкой 5% годовых приобретена с дисконтом 10%. По истечении года она была продана по цене 110% от номинала. Необходимо определить её полную доходность.

Решение:

1. Определим сумму процентов по облигации за год:

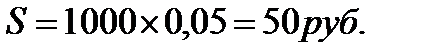
2. Цена приобретения облигации:

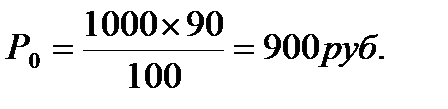
3. Курсовая стоимость облигации через год будет равна:

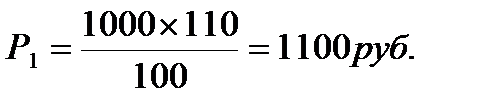
4. Таким образом, полная доходность облигации за год составит:

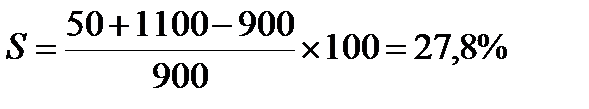
Если в условии задачи вместо стоимости покупки и продажи облигации указываются курсы покупки и продажи, и доход имеет процентное выражение, то вместо абсолютных чисел в формуле применяются относительные показатели.

Облигации имеют нарицательную (номинальную) и рыночную цену. Номинальная стоимость облигации не меняется на протяжении всего срока облигационного займа. Рыночная цена определяется как дисконтированная сумма купонного дохода и суммы к погашению. В качестве ставки дисконта принимается минимально приемлемый уровень доходности.

Порядок расчета рыночной цены облигации зависит от условий выплаты дохода. Различают облигации без выплаты купонного дохода (дисконтные), облигации с выплатой дохода через равные промежутки времени и облигации с выплатой процентов в конце срока обращения.

3. В частности для облигаций с дисконтом (нулевым купоном) рыночную стоимость можно рассчитать следующим образом (дисконтирование по схеме сложных процентов):

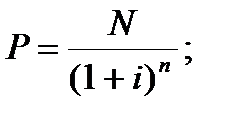
где

Р – рыночная стоимость облигации, руб;

N – номинал облигации, руб;

i – минимально приемлемый уровень доходности (ставка рыночного ссудного процента), доля;

n – период, лет.

Пример:

Коммерческий банк выпустил облигации, номиналом 15 тыс. руб. со сроком погашения через 8 лет без выплаты купонных процентов. Погашение производится по номиналу. Необходимо определить рыночную цену облигации при условии, что минимальная приемлемая ставка доходности составляет 11% годовых. На момент расчетов данная облигация продается на рынке за 6 тыс. руб.

Решение:

Подставляя данные в приведенную выше формулу, получим следующее значение рыночной стоимости облигации:

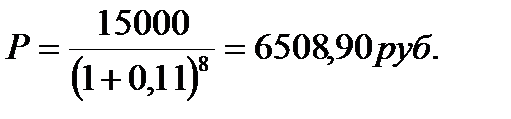
Сопоставляя рассчитанную рыночную стоимость и стоимость облигации на рынке (6508,90 > 6000), можно заключить, что данная облигация недооценена рынком, и инвесторы будут стремиться её купить, обеспечив тем самым более высокую доходность к погашению.

4. По облигациям с ежегодной выплатой процентов рыночную стоимость можно рассчитать:

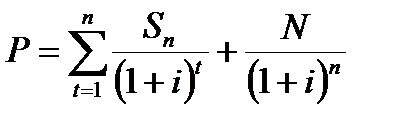
где

S_n – купонный доход за n год, руб.;

t – порядковый номер года выплаты дохода (от 1 до n).

i – минимально приемлемый уровень доходности (ставка рыночного ссудного процента), доля;

n – период, лет.

Пример:

По облигации номинальной стоимостью 12 тыс. руб. в течение 3 лет ежегодно выплачиваются процентные платежи в сумме 1,5 тыс. руб., которые могут быть помещены в банк под 9 % годовых.

Решение:

Рыночная стоимость облигации составит:

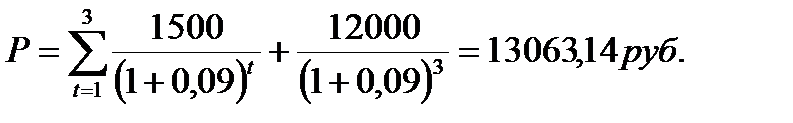
5. Рыночная стоимость облигаций, проценты у которых погашаются в конце срока обращения, определяется:

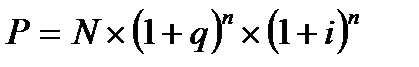
где

Р – рыночная стоимость облигации, руб.;

N – номинал облигации, руб.;

i – минимально приемлемый уровень доходности (ставка рыночного ссудного процента), доля;

n – период, лет;

q –процентная ставка по облигации, доля.

Пример:

По облигации номиналом 15 тыс. руб. со сроком погашения через 2 года проценты по ставке 8 % годовых выплачиваются в момент погашения. Приемлемая ставка доходности составляет 13 %. Определить расчетную цену облигации. На момент расчёта стоимость облигации на рынке составила 23500 руб.

Решение:

Расчетная стоимость облигации составит:

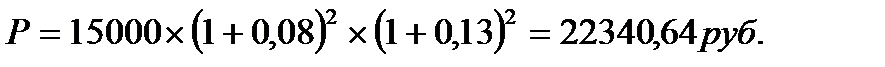
Исходя из сравнения действующей рыночной стоимости и расчетной стоимости облигации, можно предположить, что стоимость облигации переоценена рынком и инвесторы будут стремиться её продать, ожидая падения стоимости.

Важной характеристикой облигации является ее курс. Рыночные цены существенно различаются между собой. Рыночный курс

рассчитывается для достижения их сопоставимости. Он определяется исходя из значения рыночной стоимости (курсовой стоимости) и номинала облигации:

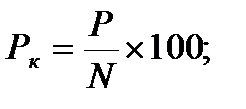
где

P_к–курс облигации;

N –номинал облигации, руб.;

Р –рыночная стоимость облигации, руб..

Пример:

Номинальная стоимость облигации составляет 10 тыс. руб., а цена приобретения облигации составила 9, 411 тыс. руб.

Решение:

На момент покупки рыночный курс облигации составит:

.

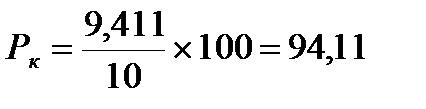Учёт векселей

Под учетом векселя понимается его передача векселедержателем банку для получения вексельной суммы до наступления даты платежа. За учёт векселя банк взимает плату, возмещая векселедержателю сумму, указанную в векселе, за вычетом учётного процента (дисконта).

По виду получаемого дохода векселя подразделяются на два типа: вексель, в котором указана абсолютная сумма (номинал), подлежащая выплате должником – это дисконтный вексель, приобретённый со скидкой; вексель, в котором, кроме абсолютной суммы долга, предусмотрено начисление процентов на указанную сумму – это процентный вексель. В каждом случае сумма, которую должен получить векселедержатель в банке, будет рассчитываться по-своему.

1. Дисконтные векселя.

;

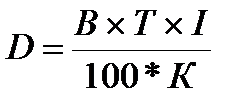где

D – сумма дисконта, руб.;

T – срок от даты учёта векселя до даты погашения, дней;

B – вексельная сумма, руб;

I – учётная ставка банка, %;

К–временная база (360 или 365 дней).

Сумма, которую получит векселедержатель (В'), определяется по формуле:

B’ =В .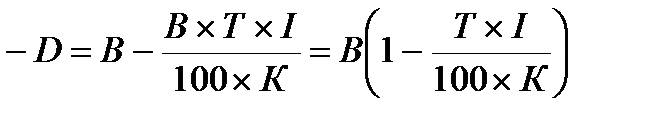

2. Процентные векселя.

Сумма, которую получит векселедержатель по процентному векселю при его учёте в банке, определяется по формуле:

,

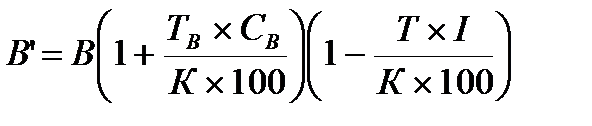где

С_в – вексельная процентная ставка;

Т_в – период обращения векселя от дня выдачи до дня предъявления к погашению.

Пример:

Вексель номинальной стоимостью 100 тыс. руб. выпущен в обращение с погашением 15 % годовых на сумму долга. Условиями выкупа предусмотрено, что он может быть предъявлен к погашению не ранее, чем через 120 дней со дня выпуска. Векселедержатель предъявил вексель банку для учёта продержав вексель 75 дней. Банк учёл вексель по ставке 20% годовых. Следует определить сумму, которую получит векселедержатель.

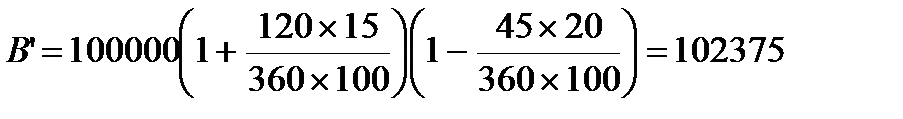руб.

Эффективность данной операции по учету векселя в банке для векселедержателя составляет:

,

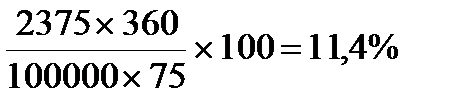т. е. ниже, чем вексельный процент, так как банк фактически кредитует векселедержателя.

Эффективность операции по учету векселя для банка составляет:

.
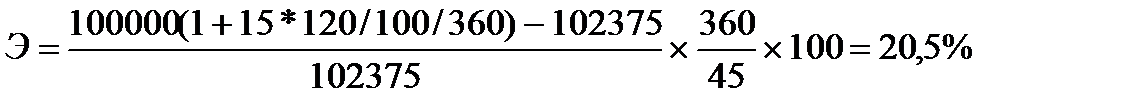