Оценка доходности и стоимости бессрочных инструментов

Ожидаемая доходность бессрочных облигаций, по которым выплачиваются “вечные” ренты, рассчитывается по формуле:

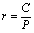, где

C – сумма ежегодных купонных выплат;

P – цена приобретения облигации.

Очевидно, что этот показатель отражает только текущую доходность, так как условиями размещения подобных займов не предусматривается выплата каких-то иных доходов. Тем не менее, никто не мешает инвестору запланировать перепродажу облигации через несколько лет владения ею по цене, которая может отличаться от цены покупки. В этом случае он сможет рассчитать доходность к погашению данного инструмента. Например, покупая за 46 фунтов стерлингов бессрочную консоль Казначейства Великобритании, по которой ежегодно выплачивается доход в сумме 4 фунта стерлингов, инвестор может рассчитывать на годовую доходность 8,696% (4 / 46). Однако, если по его “расчислению” через два года он сможет продать эту облигацию на вторичном рынке за 50 фунтов, то ее доходность к погашению (точнее, к перепродаже) должна находиться путем решения следующего уравнения:

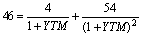
irr (а следовательно, и доходность к погашению облигации) данного денежного потока составит ≈ 12,78%. Применив приближенную формулу расчета (5.2.3), получим:

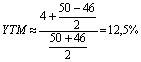
Основное отличие акций состоит в неопределенности величины ожидаемых по ним доходов. В этом смысле можно выделить привилегированные акции, дивиденды по которым, как правило, известны заранее и должны выплачиваться раньше дивидендов по обыкновенным акциям. По сути дела привилегированные акции являются промежуточной стадией между собственным (обыкновенные акции) и заемным (облигации) капиталом. Для определения их доходности используется формула, аналогичная применяемой для бессрочных облигаций:

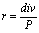, где (5.3.4)

div – сумма ожидаемых дивидендов на 1 акцию,

P – цена приобретения акции.

Точно так же, как для бессрочных облигаций, в случае планируемой перепродажи акции на вторичном рынке, полная доходность владения ею может быть определена как YTM.

Для обыкновенных акций прогнозирование величины будущих дивидендов является наиболее важной и самой сложной проблемой. Чаще всего при этом используется модель постоянного роста (модель Гордона), предполагающая неизменный в обозримом будущем темп прироста суммы дивидендов, выплачиваемы по акции. Ожидаемая доходность владения акцией в этом случае будет находиться по следующей формуле:

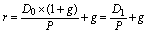, где (5.3.5)

P – цена покупки акции;

D0 – последний выплаченный дивиденд по акции;

D1 – дивиденд, ожидаемый к выплате в ближайшем периоде в будущем;

g – ожидаемый темп прироста дивиденда в будущем.

Например, на рынке имеется предложение обыкновенных акций по цене 250 рублей за 1 шт. Известно, что в прошлом году по ним был выплачен дивиденд в сумме 30 рублей на 1 акцию. В дальнейшем ожидается непрерывный рост дивиденда на 2% в год. Ожидаемая доходность акции составит:

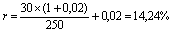
Все формулы, рассмотренные выше, строились на предположении об определенности потоков будущих доходов, выплачиваемых владельцам ценных бумаг. Однако в реальности 100%-й определенности практически никогда не существует. Даже самые надежные инструменты (например, правительственные облигации) несут в себе опасность того, что фактический результат может значительно отличаться от ожидаемого: высокая инфляция может “съесть” весь фиксированный доход по облигации, несмотря на четкое выполнение эмитентом своих номинальных обязательств. Следовательно, во всех финансовых расчетах должен присутствовать еще один важнейший параметр (о котором практически ничего не было сказано в предыдущих параграфах), характеризующий меру неопределенности, сопряженную с возможностью получения ожидаемого дохода. В финансах эта неопределенность обозначается термином риск, отражающим вероятность получения результата, отличающегося от запланированного.

[1] Шарп У., Александр Г., Бэйли Дж. Инвестиции. Глава 14 С.374-413