Задача 3. Аналитический поиск наилучшего решения

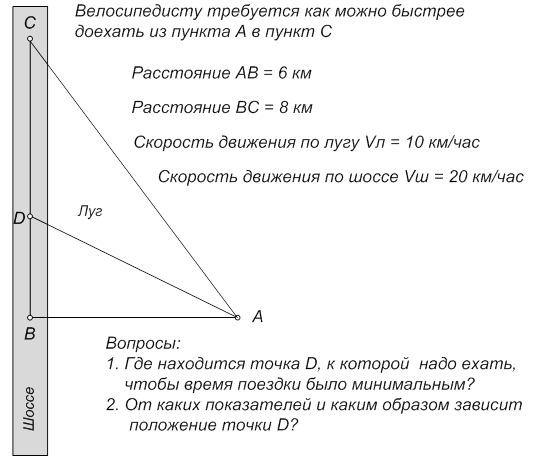
Рис. Дороги и бездорожье

Решение: Найдем аналитическую зависимость времени в пути t от заданных параметров АВ, ВС,Vл, Vш и искомого отрезка BD.

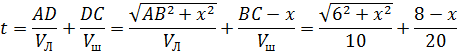
Где BD=x

Продифференцировать это выражение по параметру x и приравнять производную 0:

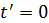
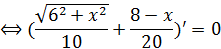
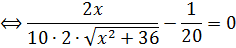
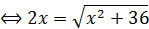
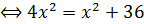
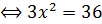
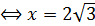км.

Точка D находится в 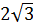км от точки B, к которой надо ехать, чтобы время поездки было минимальным.

Задача 4. Поиск наилучшего варианта путём трансформации объекта

Дана прямоугольная комната с размерами, показанными на рис. А

На потолке, на расстоянии 1 м от торцевой стены и от боковых стен сидит таракан Т. На полу, на расстоянии 1 м от противоположной торцевой стены и от боковых стен, лежит крошка хлеба К.

Определите траекторию кратчайшего пути таракана к пище (без прыжков и падений) и вычислите её длину.

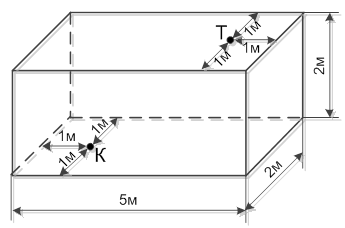
Рис. А Комната с тараканом

Решение:

Для поиска кратчайшей траектории пути таракана к пище сделаем развертку поверхности.

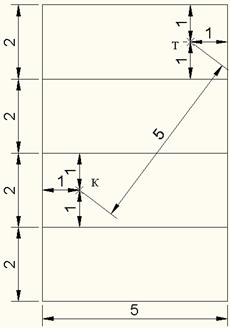
Длина кратчайшей траектории пути таракана к пище без прыжков и падений составит 5 метров.

ЗАДАЧА 5. Выбор варианта при неопределённости критерия

Когда сын падишаха повзрослел, настало время найти ему невесту. В результате первого этапа кастинга совет мудрецов отобрал четырёх самых лучших девушек. Окончательный выбор производил сам принц. Каждой из претенденток он задал один и тот же вопрос: сколько будет дважды два?

Первая претендентка сказала: «4». Вторая сказала: «5». Третья сказала: «не знаю». А четвёртая ответила: «сколько принцу будет угодно, столько и будет».

Вопрос: какую из девушек выбрал принц?

Одна из трудностей ответа на этот вопрос заключается в том, что в условиях задачи указано количество возможных вариантов (4) и результаты изучения их свойств, но несодержится точное описание критерия, в соответствие с которым следует оценивать предпочтительность вариантов. Правда, по характеру задаваемого вопроса можно предположить, что принца интересует уровень математической грамотности невест

(хотя трудно объяснить, зачем это нужно человеку, в распоряжении которого и без того имеется целый штат мудрецов и математиков).

Вторая, и главная, трудность заключается в отсутствие решающего правила,в соответствие с которым следует делать выбор.
Вообще говоря, это обстоятельство делает невозможным точное и однозначное решение поставленной задачи. В таких случаях полезно включить смекалку и внимательно рассмотреть условия задачи в поисках дополнительной информации.

Ответ: принц выбрал самую красивую девушку!

Задача 6. Выбор варианта при равнозначности оценок

Классическая задача, которую в теории принятия решений называют задачей о Буридановом осле.

Дано: Ровно посередине между двумя совершенно одинаковыми копнами сена стоит осёл. Он не может выбрать, к какой из них нужно подойти, и, в конце концов, умирает от голода.

Цель:Какой алгоритм выбора надо применить для его спасения?

При решении данной задачи мы сталкиваемся с ситуацией многоальтернативного выбора без критериев, позволяющих оценить в момент принятия решения правильность сделанного выбора. Поведение в ситуациях выбора при отсутствии критериев для осуществления этого выбора стало предметом обсуждения в философских спорах с XIV века. Тогда же возник знаменитый анекдот об осле, который, якобы, должен сдохнуть от голода между двумя одинаковыми копнами сена в случае, если он находится на равном расстоянии от них, т.е. когда у него нет никаких оснований для предпочтения того или другого копна сена.

Для решения этой задачи можно применить алгоритм случайного выбора. Если стратегия, случайно приписанная случайному выбору, окажется неудачной -то от нее всегда можно будет отказаться. Но пока не работают критерии того, какой выбор надо делать, любой конкретный выбор априорно равно эффективен (потому ведь и делается случайный выбор), а значит, и ничем не хуже любого другого выбора. Иначе говоря, неважно какой выбор сделает осел, главное, чтобы выбор был сделан.

В рамках логики самой задачи можно, однако, показать, что рационально мыслящий осёл никогда не умрёт с голоду, хотя и нельзя сказать, какую копну сена он выберет. Отказ от еды можно тоже считать выбором. Таким образом, из трёх вариантов выбора (копна слева, копна справа и голодная смерть) третий вариант будет хуже всех, поэтому осёл его не выберет никогда.