Линейные операции над свободными векторами

Понятие вектора

Определения

В различных разделах физики, механики и технических наук встречаются величины двух типов, изучаются величины разного рода. Одни величины определяются заданием их числовых значений, например, длина, площадь, объем, масса, плотность, температура и т. д. Такие величины называются обыкновенными числами или скалярами. Правила работы с этими числами рассмотрены в алгебре.

Помимо скалярных величин, в различных задачах встречаются величины, для определения которых, кроме числового значения, необходимо знать также их направление. Правила работы с этими величинами рассматриваются в векторной алгебре.

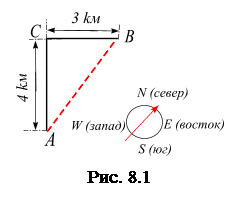Например, мы хотим определить положение путника относительно некоторой выбранной точки. Мы можем указать, сколько метров от выбранной точки до предмета, но не можем полностью определить его местоположение, пока не укажем направление, в котором он находится. Рассмотрим другой пример. Для того чтобы попасть в некоторую точку В, возможны два варианта (рис. 8.1):

1. Пройти сначала путь АС, до которого
4 kм и затем путь СВ, равный 3 kм и попасть в пункт В.

2. Если в начале пути определить, что пункт В находится к северо-востоку от пункта А и до него5 kм, томожно пройти путь АВ, равный 5 kм и попасть в пункт В.

Таким образом, положение пункта назначения от выбранной точки А нужно характеризовать численным значением (расстоянием в метрах, километрах и т. д.) и направлением, например, по компасу (рис. 8.2). Комбинация двух величин – численное значение и направление – определяет векторную величину, или просто вектор.

Вектор – это величина, которая характеризуется своим численным значением и направлением.

Часто в школьных учебниках вектором называется направленный отрезок AB, для которого указан порядок его начала и конца. С помощью векторов описываются такие физические величины, как перемещение, скорость, сила и др.; необходимость их математического описания и привела к возникновению понятия вектора. Термин был введен У. Гамильтоном в 1845 г.

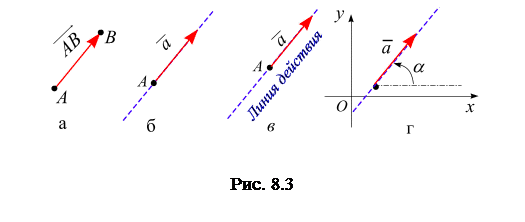Графически векторы изображают с помощью отрезка со стрелкой на конце (рис. 8.3, а). Причем длина отрезка при выбранной единице масштаба равна числовому значению векторной величины. Чтобы отрезку 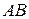, ограниченному точками А и В, прописать направление, точки А и В задаются в определенном порядке: первая точка (пишется на первом месте) называется началом вектора, вторая (пишется на втором месте) – его концом (рис. 8.3, а). Если А – начало вектора и В – его конец, то вектор обозначается 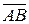или малой латинской буквой с чертой над ней, например, . Начало вектора называют точкой приложения вектора (рис. 8.3, б). Линия, вдоль которой направлен вектор, называется линией действия вектора (рис. 8.3, в).

Направление вектора можно задать в правой декартовой системе координат углом 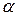, который нужно отсчитывать от положительного направления оси 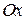против часовой стрелки (рис. 8.3, г). Направление отсчета угла играет важную роль.

В кинематической интерпретации вектор рассматривается как путь, пройденный прямолинейно движущейся точкой от начального положения А до конечного положения В.

Любой вектор характеризуется точкой приложения (точка А), длиной и линией действия. Длина вектора 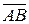называется его модулем и обозначается символом 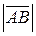. Модуль вектора обозначается 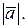Часто модуль вектора обозначается просто прописной буквой 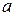. Запис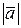и и 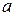равнозначны.

Вектор, модуль которого 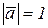, называется единичным вектором.

Вектор называется нулевым вектором (обозначается 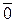), если начало вектора и конец его совпадают. Нулевой вектор направления не имеет.

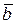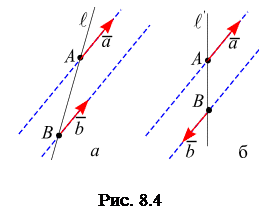
Пусть и – два вектора, расположенные на параллельных линиях действия; векторы и 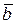могут быть направлены либо одинаково, либо противоположно (рис. 8.4, а). Это означает следующее: в первом случае направление векторов и 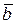одинаково относительно прямой 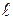, соединяющей точки приложения векторов; во втором случае – разное относительно прямой 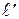, соединяющей точки приложения векторов и 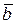(рис. 8.4, б).

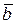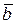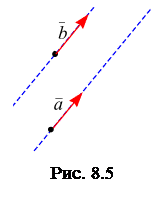
Векторы и , расположенные на одной линии действия или на параллельных линиях действия, называются коллинеарными. Замена вектора вектором , если 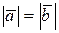, называется переносом вектора
(рис. 8.5).

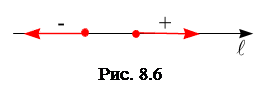
Пусть задана ось 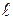с выделенным направлением , рис. 8.6. Вектор считается положительно направленным, если его направление совпадает с направлением заданной оси 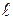и отрицательно направленным – если его направление противоположно направлению заданной оси .

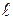Виды векторов

Разделяют три типа векторов: свободный, скользящий и связанный.

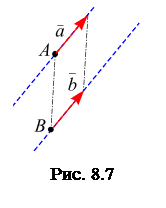
1. Свободными векторами представляются физические величины, не изменяющиеся при переходе от одной точки пространства к любой другой. Другими словами, если векторы при параллельном переносе совмещаются, то они равны (рис. 8.7).

Определение. Два свободных вектора и 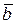называются равными, если они коллинеарны, равны по модулю и одинаково направлены. В этом случае пишут: .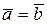

При поступательном движении твердого тела скорости в каждой точке тела равны между собой по величине и направлению. Поэтому скорость тела при поступательном движении задается одним свободным вектором, приложенным в центр тяжести этого тела (рис. 8.8). Вектор скорости –свободный вектор.

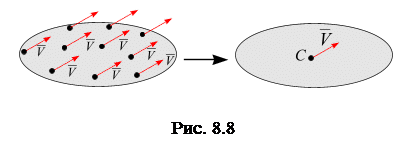
Свободным вектором называется множество всех равных векторов пространства.

2. Скользящие векторы представляют собой векторные физические величины, остающиеся неизменными вдоль линии действия вектора. Они изменяются при переходе к другой точке пространства, не лежащей на линии действия. Например, сила, приложенная к точке 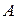абсолютно твердого тела, сообщит последнему определенное движение из начального состояния. Такое же движение сообщит сила, приложенная к произвольной точке 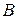, расположенной на той же линии действия (рис. 8.9).

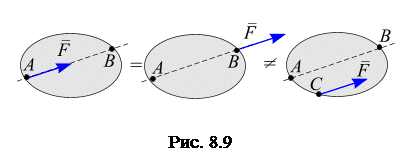
Но если эту же силу приложить к точке 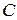не лежащей на данной линии 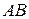, она сообщит телу иное движение.

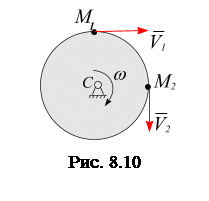3. Закрепленные векторы представляют собой физические величины, определенные только в заданной точке пространства. В других точках пространства они имеют другое значение. Например, при вращении твердого тела в плоскости вокруг неподвижного центра 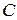вектор скорости в точке 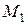– 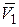и вектор скорости в точке 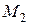– 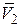являются закрепленными векторами, т. к. имеют смысл только в заданных точках пространства, рис. 8.10.

В дальнейшем будем рассматривать только свободные векторы.

Линейные операции над свободными векторами