II. Изучение нового материала. €

Работа по учебнику.

– Сегодня на уроке будем решать примеры вида 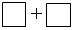= 12.

Задание 1. Сколько месяцев в году? Назовите их подряд, начиная с января.

– Сколько месяцев составляют полгода? (6 месяцев; 6 + 6 = 12.)

– С 1 января прошло полгода. Сколько месяцев осталось до следующего Нового года? (6 месяцев.)

– Сколько весенних (летних, осенних, зимних) месяцев? (3 месяца; 3 + 3 + 3 + 3 = 12 м.)

– Лето длится 3 месяца. А сколько остальных месяцев? (9 месяцев; 3 + 9 = 12 м.)

– Какой по счёту с начала года август? (Восьмой.)

– Сколько месяцев с начала учёбы до Нового года? А от Нового года до 1 сентября? (4 месяца; 8 месяцев; 8 + 4 = 12 м.)

– Школьные каникулы вместе с воскресными днями составляют 5 месяцев. Сколько месяцев в году составляют учебные дни? (7 месяцев; 5 + 7 = 12 м.)

Задание 2. Рассмотрите рисунок.

– Сколько белых клеток? (7 клеток.)

– Сколько всего клеток? (12 клеток.)

– Из равенства с суммой можно получить два равенства с разностью. (5 + 7 = 12; 12 – 5 = 7; 12 – 7 = 5.)

Запомните: 5 + 7 = 12.

– Возьмите другие суммы двух однозначных чисел, равные 12. Запишите соответствующие равенства с разностями.

9 + 3 = 12 8 + 4 = 12

12 – 9 = 3 12 – 8 = 4

12 – 3 = 9 12 – 4 = 8

– Прочитайте задачу 3. Что известно в задаче? Что требуется узнать?

Всего – 12 мес. Решение:

Лето – 3 мес. 12 – 3 = 9 (мес.) – зима на Севере.

Зима – ? мес.

– Прочитайте задачу 4. Составьте краткую запись, решите задачу.

Всего – 3 больших зв. и 9 маленьких зв.

Видны в телескоп – 8 зв.

Видны невооруженным глазом – ? зв.

Решение:

1) 9 + 3 = 12 (зв.) – всего.

2) 12 – 8 = 4 (зв.) – видны невооруженным глазом.

– Прочитайте задачу 5. Что известно? Что требуется узнать? Решите задачу, используя схему.

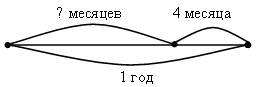
Решение: 12 – 4 = 8 (мес.).

Запомните: 9 + 3 = 12;

8 + 4 = 12.

Задание 6. Рассмотрите схему. Объясните такой способ сложения.

– Запишите равенство числами. (9 + 3 = 9 + (1 + 2) = (9 + 1) + 2 = = 10 + 2 = 12.)

– Выполните сложение таким же способом.

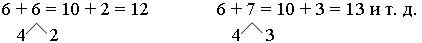
Задание 7. Рассмотрите рисунок. Прочитайте названия книг. Эти книги про 12 в жизни встретятся не раз… Вспомните, где ещё встречали вы число 12.

– Узнайте, что такое дюжина. Почему число 13 называют чертовой дюжиной? Почему 13 считают несчастливым числом?

Существует много суеверий, связанных с природой, чарами, духами, предметами, цветами, происшествиями и т. д. Вот и поверье, что число 13 – несчастливое, относится к таким.

Наверное, нет другого такого суеверия, которому в том или ином виде большинство людей придавало бы столько значения, как признание числа 13 несчастливым. В некоторых странах в гостиницах нет этажа под номером 13 – счет идет от 12-го сразу к 14-му; нет также и комнаты под номером 13. Многие люди никогда не приглашают на обед 13 человек.

Как ни странно, но не существует единственного общепринятого объяснения происхождения этого суеверия. Есть только много различных мнений по этому поводу.

Некоторые специалисты полагают, что число 13 стало непопулярным еще с тех времен, когда человек начал учиться считать. Используя 10 пальцев рук и две ноги как отдельные единицы, ему удавалось досчитать до 12. Но дальше следовало неизвестное число 13, которое пугало человека.

В христианстве число 13 и возникшее вокруг него суеверие связывается с Тайной вечерей, на которой присутствовал Христос и 12 апостолов – всего 13. Некоторые обращаются к скандинавской мифологии, к обедне у Валхаллы, куда было приглашено 12 богов. Локи, бог споров и зла, навязался тринадцатым. В результате был убит любимый из богов – Бальдер.

Вместе с тем еще одна странность числа 13 состоит в том, что оно, наоборот, считалось счастливым в Древнем Китае и Египте.

Урок 20
Состав числа 15

Цель деятельности учителя: способствовать формированию умения выполнять сложение однозначных чисел вида = 15; совершенствовать умение записывать равенства по рисунку и схеме.

Планируемые результаты образования.

Предметные:умеют выполнять сложение и вычитание чисел в пределах 20 с переходом через десяток с опорой на состав числа 15, решать текстовые задачи, в том числе в 2–3 действия, составлять выражение по условию задачи.

Личностные: оценивают собственные успехи в освоении вычислительных навыков; сопоставляют собственную оценку своей деятельности с оценкой её товарищами, учителем.

Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД):регулятивные: проверяют результаты вычислений; планируют собственную вычислительную деятельность; познавательные: устанавливают закономерности в числовых выражениях и используют их при вычислениях, ориентируются в таблице сложения; придумывают задачи в соответствии со схемой, формулируют условия задачи; ориентируются в рисунках, схемах, цепочках вычислений; коммуникативные: отвечают на вопросы, задают вопросы, уточняют непонятное.

Ход урока