Решения задач диагностической работы

ЕГЭ 2010. Математика. Задача B4. Рабочая тетрадь

Смирнов В.А.

(под редакцией А. Л. Семенова и И.В.Ященко)

М.: Издательство МЦНМО; 2010, 48 стр.

Рабочая тетрадь по математике серии «ЕГЭ 2010.Математика» ориентирована на подготовку учащихся старшей школы для успешной сдачи Единого государственного экзамена по математике в 2010 году. В рабочей тетради представлены задачи по одной позиции контрольных измерительных материалов ЕГЭ-2010.

На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по основным темам планиметрии. Рабочая тетрадь ориентирована на один учебный год, однако при необходимости позволит в кратчайшие сроки восполнить пробелы в знаниях выпускника.

Тетрадь предназначена для учащихся старшей школы, учителей математики, родителей.

http://geometry2006.narod.ru/

Содержание

Введение

Диагностическая работа ……………………………………………………..

Решения задач диагностической работы ……………………………………

Тренировочные работы ………………………………………………………

1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника ……………………………………..……

2. Нахождение значений тригонометрических функций острых углов равнобедренного треугольника ………………………………………….

3. Нахождение значений тригонометрических функций тупых углов

4. Нахождение тригонометрических функций углов, изображенных на клетчатой бумаге ……………………………… ……………………….

5. Нахождение элементов прямоугольных треугольников …………..

6. Нахождение элементов равнобедренных треугольников ……………

Самостоятельные работы ……………………………………………

Самостоятельная работа 1 ………………………………………………….

Самостоятельная работа 2 ………………………………………………….

Самостоятельная работа 3 ………………………………………………….

Ответы ……………………………………………………………………

ВВЕДЕНИЕ

Данное пособие предназначено для подготовки к выполнению задания В4 ЕГЭ по математике. Его целями являются:

– показ примерной тематики и уровня трудности геометрических задач, включенных в содержание ЕГЭ;

– проверка качества знаний и умений учащихся по геометрии, их готовность к сдаче ЕГЭ;

– развитие представлений учащихся об основных геометрических фигурах и их свойствах, формирование навыков работы с рисунком;

– повышение вычислительной культуры учащихся, подготовка их к решению геометрических задач с числовым ответом.

Пособие содержит задачи по тригонометрии. Они проверяют умения учащихся находить значения тригонометрических функций углов по известным элементам геометрических фигур и, наоборот, находить неизвестные элементы геометрических фигур по известным значениям тригонометрических функций.

Для успешного выполнения предлагаемых задач требуются знания определений тригонометрических функций и их свойств, умения работать с формулами, выполнять арифметические действия и преобразования числовых выражений.

Задачи сопровождаются рисунками, позволяющими лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления.

Вначале предлагается диагностическая работа, содержащая тригонометрические задачи, разбитые на шесть различных типов по три задачи в каждом. Для тех, кто хочет проверить правильность решения предложенных задач или убедиться в верности полученного ответа, приводятся их решения и даются ответы.

Затем, для закрепления рассмотренных методов решения задач, предлагаются тренировочные работы, каждая из которых содержит тригонометрические задачи одного типа.

В случае успешного решения этих задач можно переходить к выполнению заключительных самостоятельных работ, содержащих тригонометрические задачи разных типов.

В конце пособия даны ответы ко всем задачам.

По аналогии с рассмотренными задачами можно самим придумывать и решать тригонометрические задачи.

Отметим, что лучшим способом подготовки к ЕГЭ по геометрии являются систематические занятия по учебнику геометрии. Данное пособие не заменяет учебника. Оно может быть использовано в качестве дополнительного сборника задач при изучении геометрии в 7-9 классах, а также при организации обобщающего повторения в 10-11 классах или при самостоятельных занятиях по геометрии.

Диагностическая работа

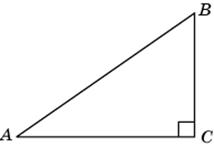
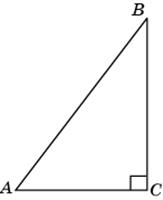
1.1. В треугольнике ABC угол C равен 90^о, AB = 10, AC = 8. Найдите sin A.

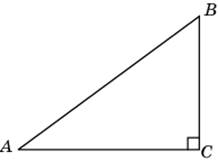1.2. В треугольнике ABC угол C равен 90^о, sin A = 0,6. Найдите cos A.

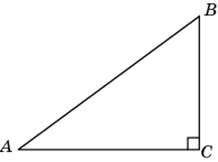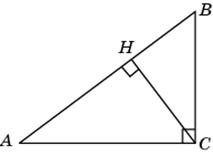
1.3. В треугольнике ABC угол C равен 90^о, высота CH равна 6, AC = 10. Найдите tg A.

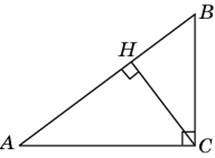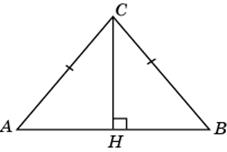
2.1.В треугольнике ABC AC = BC = 10, AB = 12. Найдите sin A.

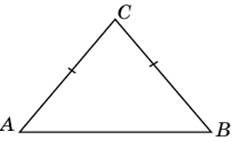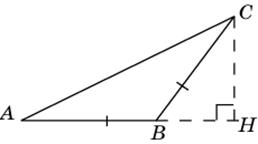
2.2. В треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите cos A.

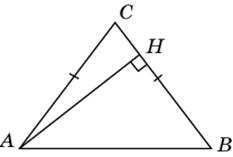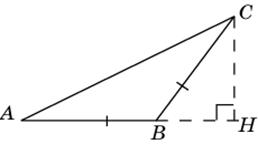
2.3. В треугольнике ABC AB = BC, высота CH равна 8, AC = 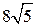. Найдите тангенс угла ACB.

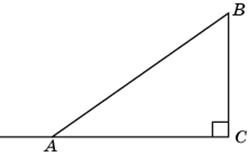
3.1. В треугольнике ABC угол C равен 90^о, AB = 10, BC = 6. Найдите синус внешнего угла при вершине A.

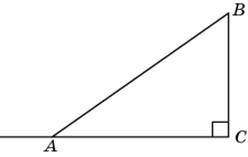3.2. В треугольнике ABC угол C равен 90^о, sin A = 0,6. Найдите косинус внешнего угла при вершине A.

3.3. В треугольнике ABC угол C равен 90^о, AB = 10, AC = 8. Найдите тангенс внешнего угла при вершине A.

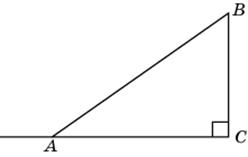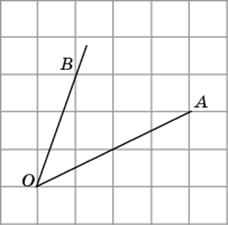
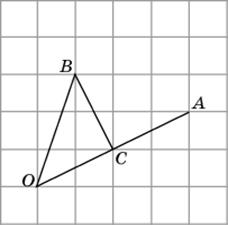
4.1. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .

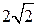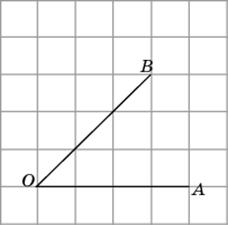4.2. Найдите тангенс угла AOB.

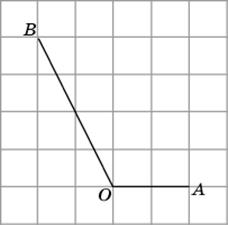4.3.Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .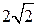

5.1. В треугольнике ABC угол C равен 90^о, BC = 4, sin A = 0,8. Найдите AB.

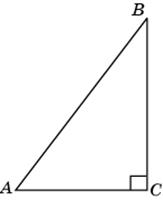5.2. В треугольнике ABC угол C равен 90^о, tg A = 0,75, AC = 8. Найдите AB.

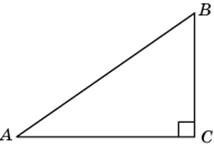5.3. В треугольнике ABC угол C равен 90^о, CH – высота, BC = 6, cos A = 0,8. Найдите CH.

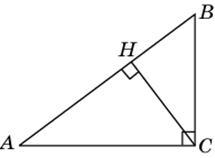6.1.В треугольнике ABC AC = BC = 10, sin A = 0,8. Найдите AB.

6.2. В треугольнике ABC AC = BC, AB = 10, cos A = 0,6. Найдите высоту AH.

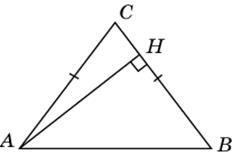6.3. В треугольнике ABC AB = BC, высота CH равна 5, tg C = 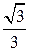. Найдите AC.

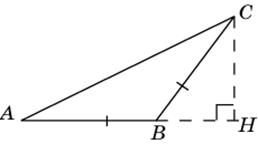Решения задач диагностической работы

1.1. Первое решение. В прямоугольном треугольнике ABC гипотенуза AB равна 10. Найдем катет BC.Используя теорему Пифагора, имеем BC = 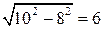. Следовательно, sin A = 0,6.

Второе решение. Так как катет AC равен 8, а гипотенуза AB равна 10, то cos A = 0,8. Воспользуемся формулой 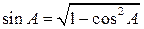, выражающей косинус через синус острого угла. Откуда sin A = 0,6.

Ответ. 0,6.

1.2. Первое решение. Воспользуемся формулой 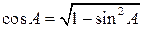. Тогда cos A = 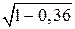= 0,8.

Второе решение. Можно считать, что гипотенуза AB и катет BC данного прямоугольного треугольника равны соответственно 10 и 6. Тогда по теореме Пифагора катет AC равен 8 и, следовательно, cos A = 0,8.

Ответ. 0,8.

1.3. В прямоугольном треугольнике ACH катет CH равен 6, гипотенуза AC равна 10. Используя теорему Пифагора, находим AH = 8. Следовательно, tg A = 0,75.

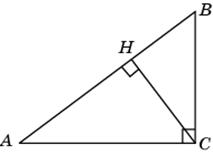Ответ. 0,75.

2.1. Проведем высоту CH.В прямоугольном треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По теореме Пифагора находим CH = 8 и, следовательно, sin A = 0,8.

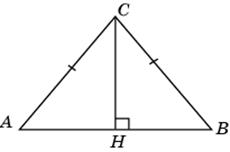Ответ. 0,8.

2.2.В прямоугольном треугольнике ABH гипотенуза AB равна 10, катет AH равен 8. По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6.

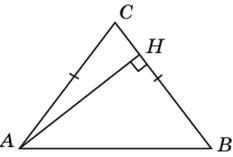Ответ. 0,6.

2.3. В прямоугольном треугольнике ACH гипотенуза AC равна 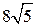, катет CH равен 8. По теореме Пифагора найдем AH. Имеем AH = 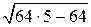= 16. Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс угла ACB равен 0,5.

Ответ. 0,5.

3.1. Синус внешнего угла при вершине A треугольника ABC равен синусу угла A и, следовательно, равен 0,6.

Ответ. 0,6.

3.2. Косинус внешнего угла при вершине A равен –cos A. Воспользуемся формулой 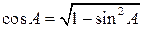, выражающей косинус острого угла через его синус. Тогда cos A = 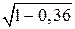= 0,8 и, следовательно, косинус внешнего угла при вершине A равен –0,8.

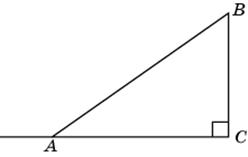Ответ. –0,8.

3.3. Тангенс внешнего угла при вершине A равен –tg A. По теореме Пифагора находим BC = 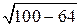= 6 и, следовательно, tg A = 0,75. Значит, тангенс внешнего угла при вершине A равен –0,75.

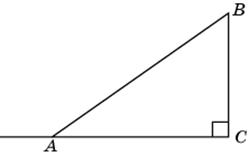Ответ. –0,75.

4.1. Первое решение.Рассмотрим прямоугольный треугольник OBC. Его катет BC равен 3, гипотенуза OB равна 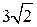. Следовательно, sin A = .

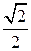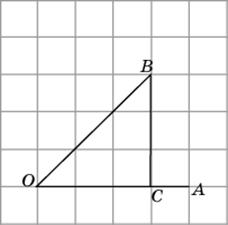Второе решение. Угол AOB равен 45^о. Следовательно, sin A = .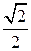

Ответ. 2.

4.2. Рассмотрим прямоугольный треугольник OBC. Его катеты BC и OC равны соответственно 4 и 2. Следовательно, тангенс угла BOC равен 2. Учитывая, что тангенс смежного угла равен тангенсу данного угла, взятому с противоположным знаком, получаем, что тангенс угла AOB равен – 2.

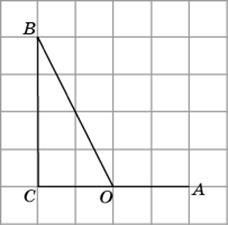Ответ. – 2.

4.3.Рассмотрим треугольник OBС. OC = BC = 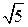, OB = 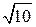. Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен .

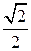Ответ. 2.

5.1.Подставляя в формулу BC = AB sin A данные значения BC и sin A, находим AB = 5.

Ответ. 5.

5.2.Имеем BC = AC 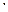tg A = 8 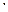0,75 = 6. По теореме Пифагора находим AB = 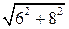= 10.

Ответ. 10.

5.3. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cos 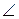BCH = 0,8. CH = BC cos BCH = 4,8.

Ответ. 4,8.

6.1.Первое решение.Проведем высоту CH. Имеем CH = AC 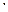sin A = 8. По теореме Пифагора находим AH = 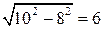и, следовательно, AB = 12.

Второе решение. Проведем высоту CH. Воспользуемся формулой 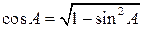, выражающей косинус острого угла через его синус. Тогда cos A = 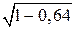= 0,6. Следовательно, AH = AC cos A = 6 и, значит, AB = 12.

Ответ. 12.

6.2. Первое решение.В равнобедренном треугольнике ABC угол A равен углу B, BH = AB cos B = 6. По теореме Пифагора находим AH = .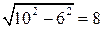

Второе решение. Воспользуемся формулой 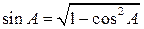, выражающей синус острого угла через его косинус. Тогда sin A = 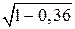= 0,8. Следовательно, поскольку в равнобедренном треугольнике A = B, получаем AH = AB sin B = 8.

Ответ. 8.

6.3. Первое решение.В равнобедренном треугольнике ABC угол A равен углу C,значит, tg A = tg C и AH = 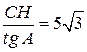. По теореме Пифагора находим AC = 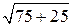= 10.

Второе решение. Так как tg C = 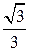, то угол C равен 30^о. Угол A равен углу C. Так как катет прямоугольного треугольника, лежащий против угла в 30^о, равен половине гипотенузы, то AC = 10.

Ответ. 10.

Тренировочные работы

1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника

1. В треугольнике ABC угол C равен 90^о, AB = 10, BC = 6. Найдите cos A.

2. В треугольнике ABC угол C равен 90^о, AB = 10, AC = 8. Найдите tg A.

3. В треугольнике ABC угол C равен 90^о, cos A = 0,8. Найдите sin A.

4. В треугольнике ABC угол C равен 90^о, cos A = 0,8. Найдите tg A.

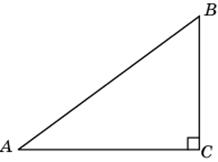
5. В треугольнике ABC угол C равен 90^о, tg A = 0,75. Найдите sin A.

6. В треугольнике ABC угол C равен 90^о, sin A = 0,6. Найдите cos B.

7. В треугольнике ABC угол C равен 90^о, cos A = 0,8. Найдите sin B.

8. В треугольнике ABC угол C равен 90^о, CH – высота, AC = 10, AH = 8. Найдите cos B.

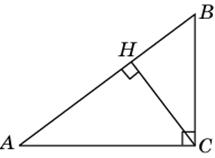9. В треугольнике ABC угол C равен 90^о, CH – высота, BC = 10, BH = 6. Найдите cos A.
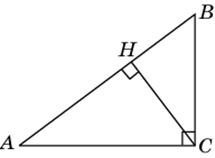