Геометрическое сложение трех векторов

Понятие суммы векторов, введенное для двух слагаемых векторов, можно обобщить на случай любого конечного числа слагаемых векторов.

Пусть, например, заданы три вектора , , 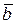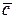(рис. 9.10, а).

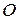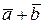Выберем на плоскости точку , затем параллельным переносом вектора перенесем его так, чтобы точка О стала началом этого вектора. Построим вначале сумму векторов . Для этого параллельным переносом вектор перенесем так, чтобы его начало совпало с концом вектора (на рис. 9.10, б это точка А).

Тогда, если

,

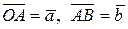то

.

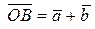Прибавив к полученной сумме вектор 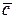, получим вектор 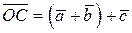. Имеем
(рис. 9.10, в):

;

.

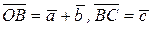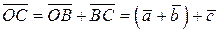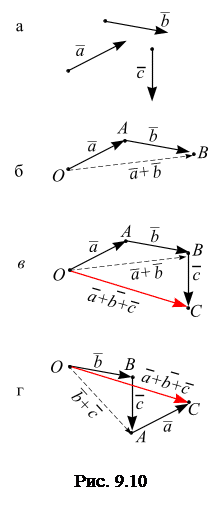
Порядок геометрического сложения векторов может быть произвольным. Из рис. 9.9, г видно, что тот же вектор 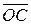можно получить, если вначале сложить векторы 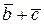, затем к полученной сумме геометрически прибавить вектор . Таким образом,

,

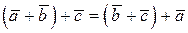т. е. сумма векторов обладает сочетательным свойством. Поэтому сумму трех векторов , , 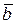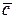записывают просто:

.

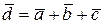Пример 9.6. Вычислить сумму трех векторов , , , 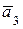приложенных в точку О, если 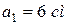, , 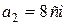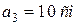. Направления векторов показаны на рис. 9.11, а.

Решение. Из произвольной точки О проводим прямую, параллельную линии действия вектора , и откладываем отрезок вдоль этой линии, равный модулю первого вектора 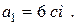Далее, через конец вектора проводим прямую, параллельную линии действия вектора (угол между линиями действия векторов и равен 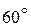), и откладываем отрезок, равный модулю второго вектора 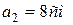; через конец вектора проводим прямую, параллельную линии действия вектора (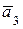угол между линиями действия векторов и 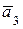равен 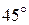), и откладываем 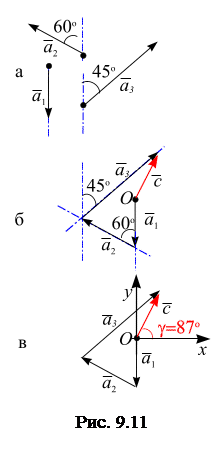отрезок, равный модулю третьего вектора 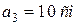. Вектор 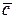, равный сумме векторов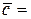 + + 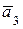, соединяет точку О (точка приложения первого вектора) с концом вектора 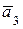(рис. 9.11, б). Измеряем линейкой модуль вектора .

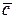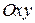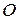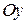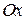Совместим начало декартовой системы координат с точкой , ось совместим с линией действия вектора (рис. 9.11, в), измерим транспортиром угол между положительным направлением оси и вектором .

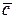В результате измерений получим величину модуля вектора 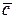и его направление относительно горизонтальной оси

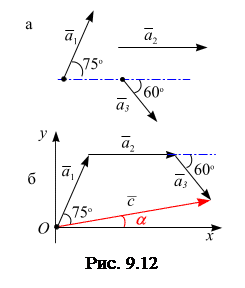
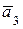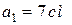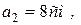
Пример 9.7. Вычислить сумму трех векторов , , , если , 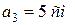. Направления векторов показаны на рис. 9.12, а.

Решение. Выберем декартову систему координат . Из точки О проводим прямую, параллельную линии действия вектора , и откладываем отрезок вдоль этой линии, равный 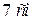(параллельный перенос). 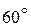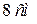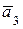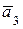Далее, через конец вектора проводим прямую, параллельную линии действия вектора (угол между линиями действия векторов и равен ), и откладываем отрезок, равный ; через конец вектора проводим прямую, параллельную линии действия вектора (угол между линиями действия векторов и равен 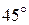), и откладываем отрезок, равный 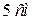. Вектор 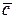, равный сумме векторов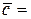 + + 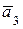, соединяет точку О (точка приложения первого вектора) с концом вектора 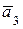(рис. 2.12, б). Измеряем линейкой модуль вектора : .

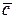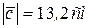Измерим транспортиром угол между положительным направлением оси 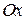и вектором : .

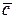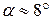В результате измерений получим величину модуля вектора 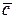и его направление относительно горизонтальной оси

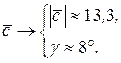
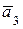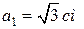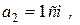
Пример 9.8.Вычислить сумму трех векторов , , , если , 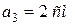. Направления векторов показаны на рис. 9.13, а.

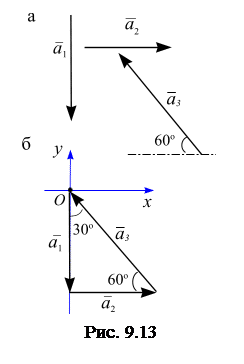Решение.Совместим начало системы координат 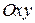с началом вектора , рис. 9.13, б. Откладываем по оси 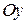отрезок, равный 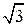(модуль первой силы),
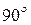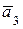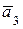рис. 9.13, б. Далее, через конец вектора проводим прямую, параллельную линии действия вектора (угол между линиями действия векторов и равен ), откладываем отрезок, равный 1 (модуль второй силы). Через конец вектора проводим прямую, параллельную линии действия вектора (угол между линиями действия векторов и равен 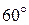), откладываем отрезок, равный 2 (модуль третьей силы).

Получили, что конец вектора 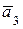совпал с началом вектора , следовательно, сумма векторов 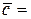+ + 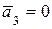. В этом случае векторный треугольник называется замкнутым (рис. 9.13, б).

Проверим полученный результат, используя теорему синусов:

.
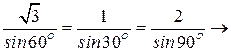
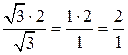