Сабақты бекітуге жаттығулар орындау.

1-сабақта сыныпта: № 65, 69

Үйге: № 66, 71

2-сабақта сыныпта: № 68, 73, 74, 76

Үйге: № 70, 75

Есептер шығару.

№65

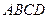Берілгені: трапеция

дм, дм

Табу керек:

Шешуі: онда параллелограмм. Параллелограмм қасиеті бойынша .

Жауабы: 28 дм

№69

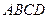Берілгені: теңбүйірлі трапеция

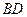мен диогональдар

Дәлелдеу керек: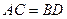

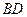Дәлелдеу: мен диогональдарын жүргіземіз.

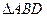мен қарастырамыз:

1) ортақ

2) теңбүйірлі трапецияның қасиеті бойынша

3) берілуі бойынша үшбұрыштар теңдігінің I белгісі бойынша, онда .

№68

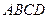Берілгені: трапеция

Табу керек:

Шешуі: болғандықтан (ішкі тұстас бұрыштар). . Сол сияқты

Жауабы:

№73

Берілгені: 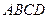теңбүйірлі трапеция

Табу керек:

Шешуі: дан ендеше (айқыш бұрыштар), деп белгілесек . Үшбұрыштың ішкі бұрыштарының қосындысы туралы теорема бойынша 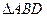-дан .

Бұдан . Жауабы:

№73

Берілгені: 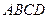теңбүйірлі трапеция

АС диогональ

, ,

Табу керек: ВС

Шешуі: (айқыш бұрыштар), ендеше 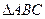теңбүйірлі

Жауабы: 3 м

№73

Берілгені: 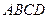теңбүйірлі трапеция

,

Табу керек:

Шешуі: түсіреміз

болғандықтан ,

Жауабы: 18 см, 34 см

Сабақты қорытындылау.

16 сабақ

Сабақтың тақырыбы:Трапецияның орта сызығы

Сабақтың мақсаты:Трапецияның орта сызығы ұғымын енгізу, анықтамасын біле отырып, қасиетін ұғындыру. Теорияны есептер шығаруда қолдана білуге үйрету.

Сабақтың түрі:Жаңа сабақты ұғындыру сабағы

Сабақтың көрнекілігі:сызбалар, плакаттағы дайын сызбалар, электронды оқулық, т.б.

Сабақтың барысы:

1. Ұйымдастыру жұмысы

2. Өтілген тақырыптар бойынша сұрақтарға жауап алу

а) Трапецияның анықтамасы

ә) Трапеция түрлері

б) Теңбүйірлі трапецияның қасиеттері

Жаңа сабақ.

Анықтама. Трапецияның бүйір қабырғаларының отасын қосатын кесіндіні трапецияның орта сызығы деп атайды.

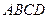трапеция

орта сызығы

Теорема. Трапецияның орта сызығы табандарына параллель және табандарының қосындысының жартысына тең.

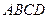Берілгені: трапеция

орта сызығы

Дәлелдеу керек:

1.

2.

Дәлелдеу: нүктесі арқылы мен табандарына параллель түзулер жүргізсек, ал бүйір қырын нүктесінде қиып өтеді. болғандықтан Фалес теоремасы бойынша . Олай болса трапецияның орта сызығы, салуымыз бойынша . Демек, теореманың бірінші бөлігі дәлелденді.

Теореманың 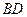диагоналін жүргізсек, Фалес теоремасы бойынша О нүктесі де 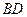кесіндісінің ортасы болады. Ендеше -ның, -ның орта сызығы болады.

. Оларды қоссақ , теорема дәлелденді.

1-2 мысалдарды қарастыру. Шешу үлгілері оқулықта көрсетілген.

Сыныпта есептер шығару.№ 91, 92

Үйге тапсырма:№ 93, 96

Есептер шығару

№ 91

Берілгені: 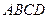трапеция

Табу керек: орта сызығы

Шешуі: Трапецияның орта сызығының қасиеті бойынша ,

Жауабы: 7,5 дм

№ 92

I жағдай.

Берілгені: кесінді, түзу

мен бір жарты жазықтықта жатыр деп алайық

-ның ортасы

Табу керек:

онда ендеше 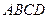трапеция, -орта сызығы

II жағдайды өз бетінше қарастырыңдар.